Книга: Основы объектно-ориентированного программирования
Наследование и утверждения
Следствия красоты базисных идей:
[x]. Связь наследования с утверждениями и Проектированием по Контракту.
[x]. Глобальная структура наследования, где все классы согласованы.
[x]. Замороженные компоненты, для которых не применим принцип Открыт-Закрыт.
[x]. Ограниченная универсальность: как задавать требования на родовые параметры.
[x]. Попытка присваивания: как безопасно приводить к типу.
[x]. Как и когда изменять свойства типа при повторных объявлениях.
[x]. Закрепленные объявления, помогающие избежать лавины переобъявлений.
[x]. Непростые отношения между наследованием и скрытием информации.
Вопросам наследования будут посвящены еще две лекции: обзор проблем типизации представлен в лекции 17, а подробное обсуждение методологии наследования - в лекции 6 курса "Основы объектно-ориентированного проектирования".
Большинство разделов этой лекции строится по единому принципу: экзаменуются следствия идей предыдущих двух лекций, обнаруживаются проблемы, они подробно анализируются, предлагается обоснованное решение. Ключевым является шаг анализа - как только проблема становится ясной, зачастую решение ее находится сразу же.
Обладая изрядной мощью, наследование может быть и опасным. Не будь механизма утверждений, создатели классов могли бы весьма "вероломно" пользоваться повторными объявлениями и динамическим связыванием для изменения семантики операций без возможности контроля со стороны клиента. Утверждения способны на большее: они дают нам боле глубокое понимание природы наследования. Не будет преувеличением сказать, что лишь понимание принципов Проектирования по Контракту позволяет в полной мере постичь сущность концепции наследования.
Вкратце мы уже очертили основные правила, управляющие взаимосвязью наследования и утверждений: все утверждения (предусловие и постусловия подпрограмм, инварианты классов), заданные в классах-родителях, остаются в силе и для их потомков. В этом разделе мы уточним эти правила и используем полученные результаты, чтобы дать новый взгляд на наследование как на субподряды (subcontracts).
Инварианты
С правилом об инвариантах класса мы встречались и прежде:
Правило родительских инвариантов
Инварианты всех родителей применимы и к самому классу.
Инварианты родителей добавляются к классу. Инварианты соединяются логической операцией and then. (Если у класса нет явного инварианта, то инвариант True играет эту роль.) По индукции в классе действуют инварианты всех его предков, как прямых, так и косвенных.
Как следствие, выписывать инварианты родителей в инварианте потомка еще раз не нужно (хотя семантически такая избыточность не вредит: a and then a есть то же самое, что a).
Полностью восстановленный инвариант класса можно найти в плоской и краткой плоской форме последнего (см. лекцию 15).
Предусловия и постусловия при наличии динамического связывания
В случае с предусловиями и постусловиями ситуация чуть сложнее. Общая идея, как отмечалось, состоит в том, что любое повторное объявление должно удовлетворять утверждениям оригинальной подпрограммы. Это особенно важно, если подпрограмма отложена: без такого ограничения на будущую реализацию, задание предусловие и постусловий для отложенных подпрограмм было бы бесполезным или, хуже того, привело бы к нежелательному результату. Те же требования к предусловию и постусловию остаются и при переопределении эффективных подпрограмм.
Анализируя механизмы повторного объявления, полиморфизма и динамического связывания, можно дать точную формулировку искомого правила. Но для начала представим типичный случай.
Рассмотрим класс и его подпрограммы, имеющие как предусловие, так и постусловие:
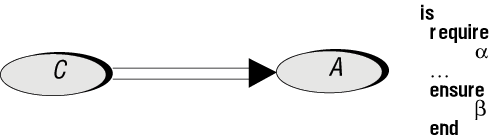
Рис. 16.1. Подпрограмма, клиент и контракт
На рис. 16.1 показан клиент C класса A. Чтобы быть клиентом, класс C, как правило, включает в одну из своих подпрограмм объявление и вызов вида:
a1: A
...
a1.r
Для простоты мы проигнорируем все аргументы, которые может требовать r, и положим, что r является процедурой, хотя наши рассуждения в равной мере применимы и к функциям.
Вызов будет корректен лишь тогда, когда он удовлетворяет предусловию. Гарантировать, что C соблюдает свою часть контракта, можно, к примеру, предварив вызов проверкой предусловия, написав вместо a1.r конструкцию:
if a1. then
a1.r
check a1.? end -- постусловие должно выполняться
... Инструкции, которые могут предполагать истинность a1.. ...
end
(Как отмечалось при обсуждении утверждений, не всегда требуется проверка: достаточно, с помощью if или без него, гарантировать выполнение условия a перед вызовом r. Для простоты будем использовать if-форму, игнорируя предложение else.)
Обеспечив соблюдение предусловия, клиент C рассчитывает на выполнение постусловия a1.? при возврате из r.
Все это является основой Проектирования по Контракту: в момент вызова подпрограммы клиент должен обеспечить соблюдение предусловия, а в ответ при возврате из подпрограммы он полагается на выполнение постусловия.
Что происходит, когда вводится наследование?
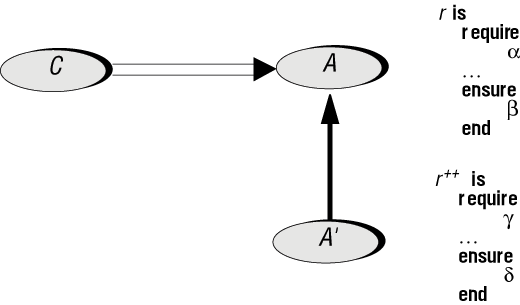
Рис. 16.2. Подпрограмма, клиент, контракт и потомок
Пусть новый класс A' порожден от A и содержит повторное объявление r. Как он может, если вообще может, заменить прежнее предусловие новым ?, а прежнее постусловие ? - новым ?
Чтобы найти ответ, рассмотрим обязательства клиента. В вызове a1.r цель a1 может - в силу полиморфизма - иметь тип A'. Однако C об этом не знает! Единственным объявлением a1 остается исходная строка
a1: A
где упоминается A, но не A'. На деле C может использовать A', даже если его автор не знает о наличии такого класса. Вызов подпрограммы r может произойти, например, в процедуре C вида:
some_routine_of_C (a1: A) is
do
...; a1.r;...
end
Тогда при вызове some_routine_of_C из другого класса в нем может использоваться фактический параметр типа A', даже если в тексте клиента C класс A' нигде не упоминается. Динамическое связывание как раз и означает тот факт, что обращение к r приведет в этом случае к использованию переопределенной версии A'.
Итак, может сложиться ситуация, в которой C, являясь только клиентом A, фактически во время выполнения использует версии компонентов класса A'. (Можно сказать, что C - "динамический клиент" A', хотя в тексте C об этом и не говорится.)
Что это значит для C? Только одно - проблемы, которые возникнут, если не предпринять никаких действий. Клиент C может добросовестно выполнять свою часть контракта, и все же в результате он будет обманут. Например,
if a1. then a1.r end
если a1 полиморфно присоединена к объекту типа A', инструкция вызовет подпрограмму, ожидающую выполнения ? и гарантирующую выполнение , в то время как клиент получил указание соблюдать и ожидать выполнения ?. Налицо возможное расхождение во взглядах клиента и поставщика на контракт.
Как обмануть клиентов
Чтобы понять, как удовлетворить клиентов, мы должны сыграть роль адвокатов дьявола и на секунду представить себе, как их обмануть. Так поступает опытный криминалист, разгадывая преступление. Как мог бы поступить поставщик, желающий ввести в заблуждение своего честного клиента C, гарантирующего при вызове и ожидающего выполнения ?? Есть два пути:
[x]. Потребовать больше, чем предписано предусловием
[x]. Гарантировать меньше, чем это следует из начального постусловия ?. Более слабое постусловие позволяет нам дать в результате меньше, чем было обещано исходной спецификацией.
| Вспомните, что мы неоднократно говорили при обсуждении Проектирования по Контракту: усиление предусловия облегчает задачу поставщика ("клиент чаще не прав"), иллюстрацией чего служит крайний случай - предусловие false (когда "клиент всегда не прав"). |
Как уже было сказано, утверждение A называется более сильным, чем B, если A логически влечет B, но отличается от него: например, x >= 5 сильнее, чем x >= 0. Если утверждение A сильнее утверждения B, говорят еще, что утверждение B слабее утверждения A.
Как быть честным
Теперь нам понятно, как обманывать. Но как же быть честным? Объявляя подпрограмму повторно, мы можем сохранить ее исходные утверждения, но также мы вправе:
[x]. заменить предусловие более слабым;
[x]. заменить постусловие более сильным.
Первый подход символизирует щедрость и великодушие: мы допускаем большее число случаев, чем изначально. Это не причинит вред клиенту, который на момент вызова удовлетворяет исходному предусловию. Второй подход означает, что мы выдаем больше, чем от нас требовалось. Это не причинит вред клиенту, полагающемуся на выполнение по завершении вызова исходных постусловий.
Итак, основное правило:
Правило (1) Утверждения Переобъявления (Assertion Redeclaration)
При повторном объявлении подпрограммы предусловие может заменяться лишь равным ему или более слабым, постусловие - лишь равным ему или более сильным.
Это правило отражает тот факт, что новый вариант подпрограммы не должен отвергать вызовы, допустимые в оригинале, и должен, как минимум, представлять гарантии, эквивалентные гарантиям исходного варианта. Он вправе, хоть и не обязан, допускать большее число вызовов или давать более сильные гарантии.
Как явствует из названия, это правило применимо к обеим формам повторного объявления: переопределению и реализации отложенного компонента. Второй случай важен особо, - утверждения будут связаны со всеми эффективными версиями потомков.
Утверждения подпрограммы, как отложенной, так и эффективной, задают ее семантику, применимую к ней самой и ко всем повторным объявлениям ее потомков. Точнее говоря, они специфицируют область допустимого поведения подпрограммы и ее возможных версий. Любое повторное объявление может лишь сужать эту область, не нарушая ее.
Как следствие, создатель класса должен быть осторожным при написании утверждений эффективной подпрограммы, не привнося излишнюю спецификацию (overspecification). Утверждения должны описывать намерения подпрограммы, - ее абстрактную семантику, - но не свойства реализации. Иначе можно закрыть возможность создания иной реализации подпрограммы у будущих потомков.
Пример
Предположим, я написал класс MATRIX, реализующий операции линейной алгебры. Среди прочих возможностей я предлагаю своим клиентам подпрограмму расчета обратной матрицы. Фактически это сочетание команды и двух запросов: процедура invert инвертирует матрицу, присваивает атрибуту inverse значение обратной и устанавливает логический атрибут inverse_valid. Значение атрибута inverse имеет смысл тогда и только тогда, когда inverse_valid является истинным; в противном случае матрицу инвертировать не удалось, так как она вырождена. В ходе нашего обсуждения случай вырожденной матрицы мы можем проигнорировать.
Конечно же, я могу найти лишь приближенное значение обратной матрицы и готов гарантировать определенную точность расчетов, однако, не владея численными подпрограммами в совершенстве, буду принимать лишь запросы с точностью не выше 10-6. В итоге, моя подпрограмма будет выглядеть приблизительно так:
invert (epsilon: REAL) is
-- Обращение текущей матрицы с точностью epsilon
require
epsilon >= 10 ^ (-6)
do
"Вычисление обратной матрицы"
ensure
((Current * inverse) |-| One) <= epsilon
end
Постусловие предполагает, что класс содержит инфиксную функцию infix "|-|" такую, что m1 |-| m2 есть |m1 - m2| (норма разности матриц m1 и m2), а также функцию infix "*", результатом которой является произведение двух матриц. One - единичная матрица.
Как человек негордый, летом я приглашу программиста, и он перепишет мою подпрограмму invert, используя более удачный алгоритм, лучше аппроксимирующий результат и допускающий меньшее значение epsilon (как повторное объявление, эта запись синтаксически некорректна:
require
epsilon >= 10 ^ (-20)
...
ensure
((Current * inverse) |-| One) <= (epsilon / 2)
Автор новой версии достаточно умен, чтобы не переписывать MATRIX в целом. Изменения коснутся лишь нескольких подпрограмм. Они будут включены в состав порожденного от MATRIX класса NEW_MATRIX.
| Если повторное объявление содержит новые утверждения, они должны иметь иной синтаксис, нежели приведенный выше. Правило появится чуть позднее. |
Изменения, внесенные в утверждения, удовлетворяют правилу повторного объявления: новое предусловие epsilon >= 10 ^ (-20) слабее исходного epsilon >= 10 ^ (-6), новое же постусловие сильнее сформулированного вначале.
Вот как все должно происходить. Клиент исходного класса MATRIX запрашивает расчет обратной матрицы именно у него, но на деле - ввиду динамического связывания - вызывает реализацию класса NEW_MATRIX. Тот же клиент может иметь в своем составе подпрограмму
some_client_routine (m1: MATRIX; precision: REAL) is
do
... ; m1.invert (precision); ...
-- Возможен вызов версии как MATRIX, так и NEW_MATRIX
end
которой один из его собственных клиентов передает первый параметр типа NEW_MATRIX.
NEW_MATRIX должен воспринимать и корректно обрабатывать любой вызов, который принимается его предком. Используя более слабое предусловие и более сильное постусловие, мы корректно обработаем все обращения клиентов MATRIX и предложим своим клиентам решение, лучше прежнего.
При усилении предусловия invert, например, epsilon >= 10 ^ (-5), вызов, корректный для класса MATRIX, мог стать теперь некорректным. При ослаблении постусловия возвращаемый результат стал бы хуже, чем гарантируемый для MATRIX.
Устранение посредника
Последний комментарий указывает на весьма интересное следствие правила Утверждений Переобъявления. В общей схеме
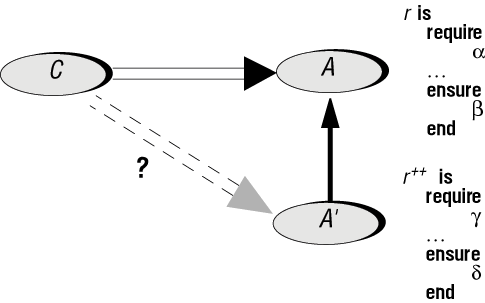
Рис. 16.3. Подпрограмма, клиент и подрядчик
утверждения ? и , введенные при повторном объявлении, предпочтительнее для клиентов, если они отличаются от и ? (предусловия - более слабые, постусловия - более сильные). Но клиент класса A, использующий A' благодаря полиморфизму и динамическому связыванию, не может в полной мере воспользоваться более выгодным контрактом, ибо единственный контракт клиента заключен с классом A.
Воспользоваться преимуществом нового контракта можно лишь став непосредственным клиентом A' (пунктирная связь с вопросительным знаком на рисунке 16.3), как в случае:
a1: A'
...
if a1.? then a1.r end
check a1. end -- постусловие выполняется
При этом вы, естественно, объявляете a1 как объект типа A', а не объект типа A, как прежде. В результате теряется универсальность полиморфизма, идущая от A.
Компромисс ясен. Клиент класса MATRIX должен обеспечивать выполнение исходного (более сильного) предусловия, а в ответ вправе ожидать выполнения исходного (более слабого) постусловия. Даже если его запрос динамически подготовлен к обслуживанию классом NEW_MATRIX, воспользоваться новыми возможностями - большей толерантностью входа и большей точностью выхода - ему никак не удастся. Для обращения к улучшенной спецификации клиент должен объявить матрицу типа NEW_MATRIX, тем самым, потеряв доступ к иным порожденным от MATRIX реализациям, не являющимся производными классами самого NEW_MATRIX.
Субподряды
Правило Утверждения Переобъявления великолепно сочетается с теорией Проектирования по Контракту.
Мы видели, что утверждения подпрограммы описывают связанный с ней контракт, в котором клиент гарантирует выполнение предусловия, получая право рассчитывать на истинность постусловия; для поставщика все наоборот.
Наследование совместно с повторным объявлением и динамическим связыванием приводит к созданию субподрядов. Приняв условия контракта, вы не обязаны выполнять его сами. Подчас вы знаете кого-то еще, способного сделать это лучше и с меньшими издержками. Так происходит, когда клиент запрашивает подпрограмму из MATRIX, но благодаря динамическому связыванию может на этапе выполнения фактически вызывать версию, переопределенную в потомке. "Меньшие издержки" означают здесь более эффективную реализацию, как в знакомом нам примере с периметром прямоугольника, а "лучше" - усовершенствование утверждений, в описанном здесь смысле.
Правило Утверждения Переобъявления просто устанавливает, что честный субподрядчик, приняв условия контракта, должен выполнить работу на тех же условиях, что и подрядчик или лучших, но никак не худших.
С позиции Проектирования по Контракту, инварианты классов - это ограничения общего характера, применимые и к подрядчикам, и к клиентам. Правило родительских инвариантов отражает тот факт, что все подобные ограничения передаются субподрядчикам.
Свое истинное значение для ОО-разработки наследование приобретает лишь совместно с утверждениями и двумя приведенными выше правилами. Метафора контрактов и субподрядов - прекрасная аналогия, помогающая разрабатывать корректное ОО-ПО. Несомненно, в этом - одна из центральных идей теории проектирования.
Абстрактные предусловия
Правило ослабления предусловий может оказаться чересчур жестким в случае, когда наследник понижает уровень абстракции, характерный для его предка. К счастью, есть легкий обходной путь, полностью согласующийся с теорией.
Типичным примером этого является порождение BOUNDED_STACK от универсального класса стека (STACK). Процедура занесения в стек элемента (put) в порожденном классе имеет предусловие count <= capacity, где count - текущее число элементов в стеке, capacity - физическая емкость накопителя.
В общем понятии стека нет понятия емкости. Поэтому создается впечатление, будто при переходе к BOUNDED_STACK предусловие приходится усилить (от бесконечной емкости перейти к конечной). Как выстроить структуру наследования, не нарушая правило Утверждения Переобъявления?
Ответ становится очевиден, если мы ближе познакомимся с требованиями к клиенту. То, что нужно сохранить или ослабить, не обязательно является конкретным предусловием, как оно видится в реализации поставщика (реализация это его забота), но касается предусловия, как оно видится клиенту. Пусть процедура put класса STACK имеет вид:
put (x: G) is
-- Поместить x на вершину.
require
not full
deferred
ensure
...
end
где функция full всегда возвращает ложное значение, а значит, стек по умолчанию никогда не бывает полным.
full: BOOLEAN is
-- Заполнено ли представление стека?
-- (По умолчанию, нет)
do Result := False end
Тогда в BOUNDED_STACK достаточно переопределить full:
full: BOOLEAN is
-- Заполнено ли представление стека?
-- (Да, если число элементов равно емкости стека)
do Result := (count = capacity) end
Предусловие, такое как not full, включающее свойство, которое переопределяется потомками, называется абстрактным (abstract) предусловием.
Такое использование абстрактных предусловий для соблюдения правила Утверждения Переобъявления может показаться обманом, однако это не так. Несмотря на то, что конкретное предусловие фактически становится более сильным, абстрактное предусловие не меняется. Важно не то, как реализуется утверждение, а то, как оно представлено клиентам в интерфейсе класса (краткой или плоско-краткой форме). Предваренный условием вызов
if not s.full then s.put (a) end
будет корректен независимо от вида STACK, присоединенного к s.
Впрочем, есть доля справедливой критики этого подхода, так как он вступает в противоречие с принципом Открыт-Закрыт. При проектировании класса STACK мы должны предвидеть ограниченную емкость отдельных стеков. Не проявив должной предусмотрительности, нам придется вернуться к проектированию STACK и изменить интерфейс класса. Это неизбежно. Из следующих двух свойств только одно должно выполняться:
[x]. ограниченный стек является стеком;
[x]. в стек всегда можно добавить еще один элемент.
Если предпочесть первое свойство и допускать порождение BOUNDED_STACK от STACK, мы должны согласиться с тем, что общее понятие стека включает предположение о невозможности в ряде случаев выполнить операцию put, абстрактно выраженное запросом full.
| Было бы ошибкой включить в виде постусловия подпрограммы full в классе STACK выражение Result = False или (придерживаясь рекомендуемого стиля, эквивалентный ему) инвариант not full. Это - случай излишней спецификации, ограничивающей свободу реализации компонентов потомками класса. |
Правило языка
Правило Утверждений Переобъявления, так как оно сформулировано, является концептуальным руководством. Как преобразовать его в безопасное и проверяемое правило языка?
В принципе, чтобы убедиться в том, что старые предусловия влекут новые, а новые постусловия - старые, следует провести логический анализ тех и других утверждений. К сожалению, это требует наличия сложного механизма доказательства теорем (несмотря на десятилетия исследований в области искусственного интеллекта). Его применение в компиляторе пока не реально.
К счастью, возможно простое техническое решение. Нужное нам правило можно сформулировать через простое лингвистическое соглашение, основанное на том наблюдении, что для любых утверждений a и b:
[x]. влечет
[x]. ? and
Итак, гарантируется, что новое предусловие слабее исходного либо равно ему, если оно имеет вид
Правило (2) Утверждения Переобъявления
При повторном объявлении подпрограммы нельзя использовать предложения require или ensure. Вместо них следует использовать предложение, начинающееся с:
[x]. require else, объединенное с исходным предусловием логической связкой or
[x]. ensure then, объединенное с исходным постусловием логической связкой and.
При отсутствии таких предложений действуют исходные утверждения.
Заметим, что используются нестрогие булевы операторы and then и or else, а не обычные and и or, хотя чаще всего это различие несущественно.
Иногда получаемые утверждения могут оказаться сложнее, чем необходимо на самом деле. В примере с подпрограммой обращения матриц, где исходным было утверждение
invert (epsilon: REAL) is
-- Обращение текущей матрицы с точностью epsilon
require
epsilon >= 10 ^ (-6)
...
ensure
((Current * inverse) |-| One) <= epsilon
мы не вправе в повторном объявлении использовать require и ensure, поэтому результат
примет вид
...
require else
epsilon >= 10 ^ (-20)
...
ensure then
((Current * inverse) |-| One) <= (epsilon / 2)
а стало быть, предусловие формально станет таким: (epsilon >= 10 ^ (-20)) or else (epsilon >= 10 ^ (-6)).
Ситуация с постусловием аналогична. Такое расширение не имеет особого значения, поскольку преобладает более слабое предусловие или более сильное постусловие. Если ? влечет , то
Повторное объявление функции как атрибута
Правило Утверждения Переобъявления нуждается в небольшом дополнении ввиду возможности при повторном объявлении задать функцию как атрибут. Что произойдет с предусловием функции и ее постусловием, если таковые имелись?
Атрибут доступен всегда, а потому мы вправе считать, что его предусловие равно True. В итоге можно полагать, что предусловие атрибута, согласно правилу Утверждения Переобъявления, было ослаблено.
Но атрибут не имеет постусловий. Мы же должны гарантировать, что он наделен всеми свойствами, заданными исходной функцией. Поэтому (в дополнение к правилу Утверждения Переобъявления) будем считать, что в этом случае автоматически постусловие добавляется к инварианту класса. Плоская форма класса будет содержать это условие в составе своего инварианта.
| Для функции без параметров, формулируя некое свойство ее результата, вы всегда можете выбрать, включать ли его в постусловие или в инвариант. С точки зрения стиля предпочтительно пользоваться инвариантом. Соблюдение этого правила позволит отказаться от внесения изменений в утверждения в будущем, если при повторном объявлении функция становится атрибутом. |
Замечание математического характера
Неформально, правило Утверждения Переобъявления гласит: "Повторное объявление утверждений может лишь сужать область допустимого поведения, не нарушая ее". Сейчас, завершая обсуждение этой темы, приведем строгую формулировку данного свойства.
Пусть подпрограмма реализует частичную функцию r, отображающую множество возможных входных состояний I в множество возможных выходных состояний O. Утверждения подпрограммы определяют правила действия r и ее возможных переопределений.
[x]. Предусловие задает область определения DOM функции r (подмножество I, на котором r гарантированно вырабатывает результат).
[x]. Постусловие задает для каждого x из DOM подмножество RESULTS(x) множества O, такое, что r (x)
Правило Утверждения Переобъявления означает, что повторное объявление может расширять область определения и сужать множество результатов. Пометив новые множества знаком ', запишем требования, закрепленные этим правилом:
DOM' DOM
RESULTS' (x) RESULTS (x) для всех x из DOM
Предусловие устанавливает, что подпрограмма и ее повторные объявления, как минимум, должны принимать некоторые входы (DOM), хотя повторные объявления могут это множество и расширить. Постусловие говорит, что результаты, возвращаемые подпрограммой и ее повторными объявлениями, могут, самое большее, содержать значения из RESULTS(x), однако, постусловия при повторных объявлениях могут это множество сузить.
В этом описании состояние системы в период выполнения определяется состоянием (значениями) всех достижимых объектов. Кроме того, входные состояния (элементы I) также включают в себя значения аргументов. Более подробное введение в математическое описание программ и языков программирования см. в [M 1990].
- Утверждения (Assertions)
- Инструкция утверждения
- У14.4 Наследование без классов
- Утверждения как средство для написания корректного ПО
- IV. Рисунки для утверждения планов
- Наследование
- Лекция 9. Наследование и замыкание
- Лекция 14. Введение в наследование
- Лекция 15. Множественное наследование
- Дублируемое наследование
- ГЛАВА 11 Наследование
- Утверждения




