Книга: Вычислительное мышление: Метод решения сложных задач

Как же это работает?

Как же это работает?

Оказывается, сбрасывая карты таким образом, вы поступаете как фокусник, сдающий карты по принципу «шиворот-навыворот». Чтобы это увидеть, нужно снова подключить и с его помощью найти точное объяснение происходящему.

Возьмите первый раунд, когда вы сбрасываете карты и одновременно ищете номер 16. Стряхнув первые перфокарты и затем избавившись от них, вы отметаете все карты с вырезом (1) в первой позиции двоичного числа. Это столбик единиц. У чисел 1, 3, 5, 7 будет вырез (1) в этой позиции — все это нечетные числа. Происходит то же самое, что и в первом раунде «шиворот-навыворот», когда мы сбрасываем каждую вторую карту. Как вы видели выше, мы переводим число из двоичной системы в десятичную, складывая числа в соответствующих разрядах (например, 5 = 4 + 0 + 1). Этот последний разряд единиц полностью определяет нечетные числа, в то время как все остальные — четные (2, 4, 8, 16, ).

Вот еще один способ понять, почему двоичное представление ведет к тому, что нечетные числа отбрасываются, — он поможет нам понять, как работает остальная часть фокуса. Подумайте, как мы считаем в двоичной системе: 0, 1, 2, 3, 4, … — это 000, 001, 010, 011, 100, … В колонке единиц во время счета значение меняется через раз, то есть в этой последней позиции по очереди оказываются 0, 1, 0, 1 — и так далее. Это значит, что если мы отбросим все единицы, то избавимся от каждой второй карты.

То есть мы показали, что в первом раунде происходит то же самое, что и в фокусе. Отбросив все карты с нечетными цифрами, мы переходим к следующему отверстию на перфокарте и, таким образом, к следующей позиции в двоичном числе. Эта операция убирает все числа, в составе которых есть разряд двоек. Например, это 6 (110 в двоичной системе), поскольку 6 = 4 + 2 + 0. На этот раз уходят 2 (10 в двоичной системе), 3 (11), 6 (110), 7 (111), 10 (1010), 11 (1011) и так далее. Однако нечетные числа уже были удалены, значит, на этот раз мы стряхнем 2, 6, 10, ... То есть остается каждая вторая карта. Это та же последовательность карт, которую мы удаляем во втором раунде «шиворот-навыворот».

Причина становится очевидной, если посмотреть на второй столбик в числах, записанных двоичным кодом. Там мы видим 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1 .

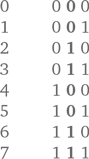
Получается, что в двоичной записи второй символ меняется только в том случае, если в первой позиции уже были и 0, и 1. Но если убрать каждую вторую карту в этой последовательности, у нас остается не 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1 ..., а 0, 1, 0, 1, 0, 1, ... И мы получаем:

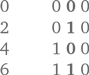
Взяв перфокарты, оставшиеся на этом этапе, мы, по сути, повторяем то же самое, что и в первом раунде, — сбрасывая все карты с 1, мы убираем каждую вторую карту, поскольку 1 стоит в середине каждого второго числа в приведенной последовательности.

То же происходит с оставшимися картами в последующих раундах. Мы всегда стряхиваем каждую вторую карту из оставшихся. Разница здесь в том, что числа на перфокартах отражают не позицию карты, но ее маркировку отверстиями и вырезами. То есть их можно перемешать, и мы все равно найдем нужную перфокарту. Еще одно различие состоит в том, что перфокарты убираются в один прием — параллельно. Метод «шиворот-навыворот» был очень медленным и скучным, потому что приходилось разбираться с каждой картой по очереди. Версия с перфокартами очень быстрая.

С точки зрения информатики в нашем фокусе используется : мы выполняем одну операцию за один прием, перемещая карту за картой. Большинство компьютерных программ написаны именно так — инструкции выполняются одна за другой. Поиск перфокарт — пример Вместо того чтобы делать одну вещь за раз, мы, по крайней мере на некоторых этапах, делаем много вещей одновременно, сбрасывая много карт. Игральные карты сдаются довольно медленно, а перфокарты отсеиваются быстро. Параллельные алгоритмы — будущее программирования. С каждым новым поколением информационных технологий нам доступно все больше процессоров как в компьютерах, так и в других электронных приборах, окружающих нас, потому что технологические возможности растут. Это относится и к так называемым — когда на одном чипе работает несколько компьютеров. Кроме того, мы можем создавать еще более масштабные компьютерные сети, которые способны эффективно работать над решением одной проблемы. Поэтому, чтобы добиться большей производительности, нужно писать алгоритмы так, чтобы все доступные процессоры всегда были заняты чем-то полезным, то есть нам необходимы параллельные алгоритмы.

Еще одна причина, по которой алгоритм с перфокартами работает быстро, — применение подхода к поиску. Этот случай похож на рассматриваемый нами в предыдущей главе. Более того, мы продолжаем говорить об алгоритмах поиска — с некоторым Мы ищем игральную карту и перфокарту. «Разделять и властвовать» — широкий способ решать задачи очень быстро, и он бывает полезен не только в ситуациях, связанных с поиском. Как мы видели, секрет здесь в том, чтобы многократно сокращать задачу вполовину. Что это значит в случае с нашими картами? В каждом раунде мы убираем половину имеющихся карт. Как мы проводим поиск среди оставшихся? Делаем то же самое — убираем половину, и еще половину, и еще половину. Однако здесь деление пополам происходит в двоичной записи чисел, а не физически.

Осознав, что перед нами проблема поиска, мы понимаем, что есть и другие способы поиска перфокарты — например, решения, действенность которых мы видели в предыдущей главе. Самое простое — проверять каждую карту по очереди. Это Наш алгоритм «разделяй и властвуй» дает результат гораздо быстрее потому, что на каждом этапе задача сокращается наполовину. Если бы карты были расположены по порядку, мы могли бы использовать для обнаружения нужной карты. Это быстрый способ, однако наш новый способ в этой ситуации еще быстрее — он действует даже в том случае, если перфокарты перетасованы.

Оглавление книги