Книга: Статистика и котики

Глава 7. Что делать, если котик заболел или критерии различий для связанных выборок

Глава 7.

Что делать, если котик заболел

или критерии различий для связанных выборок

Если ваш котик заболел, то его, разумеется, надо лечить. И, как правило, мы делаем это с помощью лекарств. Однако лекарство — штука сложная. Одним котикам оно поможет, на других не повлияет, третьим же может стать хуже.

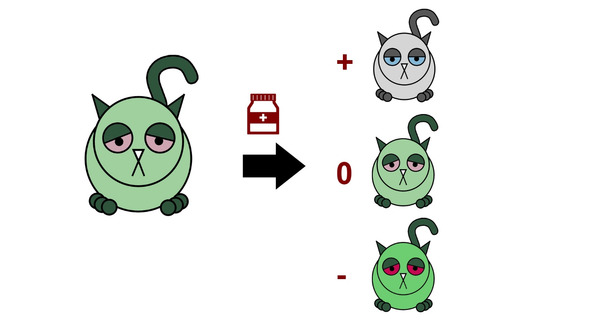
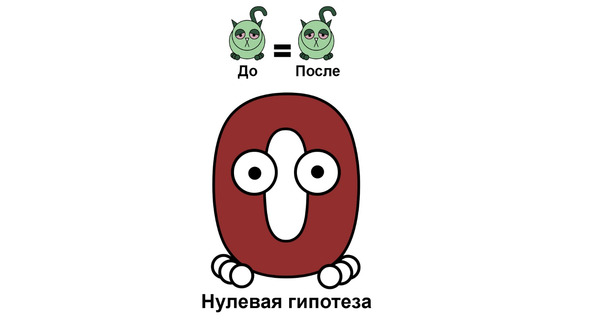
Отсюда вопрос: как понять, можно ли давать лекарство заболевшему котику или нет? Ответ на него могут дать меры различий для связанных выборок. Нулевая гипотеза таких критериев — после приема лекарств состояние котиков не изменится.

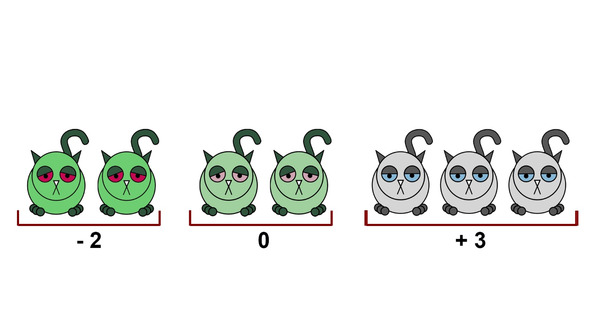
Первое, что приходит в голову, это посчитать количество котиков, которые выздоровели, и число котиков, которым стало хуже, а затем сравнить эти показатели между собой. Котики, на которых лекарство не повлияло, обычно не учитываются.

Такой подход вполне справедлив, и соответствующий метод называется критерием знаков. Однако на практике он применяется нечасто, поскольку не позволяет определить, насколько сильно изменилось состояние котиков.

Гораздо чаще мы можем встретить вариант уже известного нам критерия Стьюдента — t-критерий для связанных (зависимых) выборок. Идея тут также довольно проста. Сначала мы считаем разности между состоянием каждого котика до и после приема лекарств. Затем мы находим среднее значение от этих разностей.

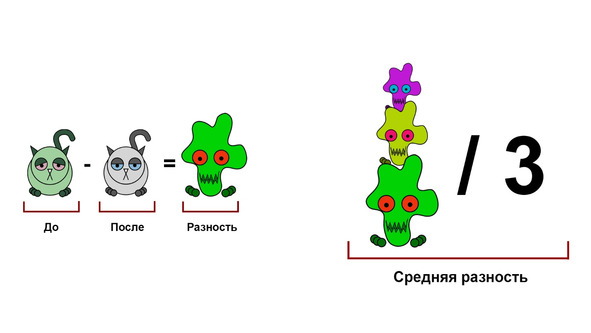
Очевидно, что чем больше это значение, тем сильнее улучшилось или ухудшилось среднее состояние котиков. Если же одной половине котиков стало лучше, а другой — ровно настолько же хуже, то средняя разность будет равна 0.

Завершающим этапом для вычисления t-критерия будет деление средней разности на стандартную ошибку этой разности. Как и с обычным критерием Стьюдента, это необходимо для приведения значения к некоторой стандартной размерности. Правда, сама стандартная ошибка считается здесь немного по-другому.

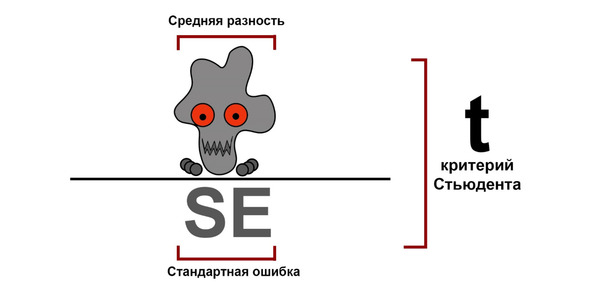
Однако заметим, что, будучи параметрическим (т. е. использующим в своей формуле среднее значение), этот критерий плохо реагирует на выбросы. Поэтому если таковые есть, используйте его непараметрический аналог — T-критерий Вилкоксона. Он немного напоминает рассмотренный ранее U-критерий Манна-Уитни.

Итак, чтобы его найти, вычислим разности между состоянием до и после (как и в t-критерии Стьюдента). Затем поставим эти разности в один ряд, от самой большой до самой маленькой, назначив им ранги. При этом знак разности не учитывается.

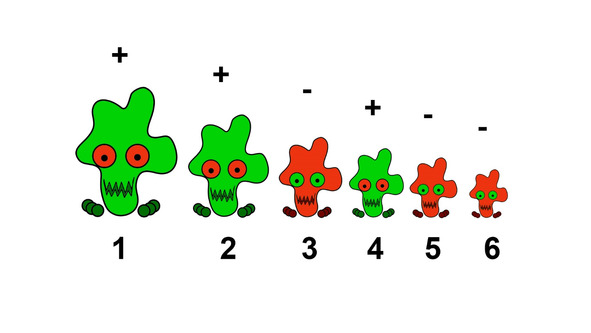
Теперь снова разделим разности на положительные и отрицательные и посчитаем суммы рангов. Логика здесь такая: чем сильнее суммы рангов будут различаться между собой, тем сильнее улучшается или ухудшается состояние котиков.

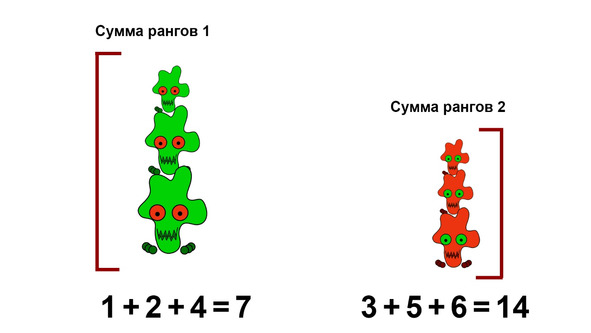
Сам T-критерий можно получить, либо посмотрев на сумму рангов для нетипичных сдвигов (т. е. более редких изменений состояния котиков), либо с помощью хитрой формулы, которую мы здесь приводить, пожалуй, не будем.

Помимо этих довольно простых методов, для связанных выборок существует свой вариант дисперсионного анализа. Однако о нем мы поговорим уже в следующей главе.

НЕМАЛОВАЖНО ЗНАТЬ!

Эксперимент и как его обработать

Как правило, проверка эффективности того или иного лекарства несколько сложнее, чем описывалось выше. Ведь котики могут выздоравливать и естественным путем. И если мы просто смотрим, как меняется их состояние, то мы не можем быть до конца уверенными, что сильнее повлияло на них — лекарство или их собственный иммунитет.

Для того чтобы разделить эти влияния, проводят специальную процедуру, называемую экспериментом. Для эксперимента требуется две группы котиков — экспериментальная и контрольная. Первой мы даем лекарство, а вторая лечится своими силами.

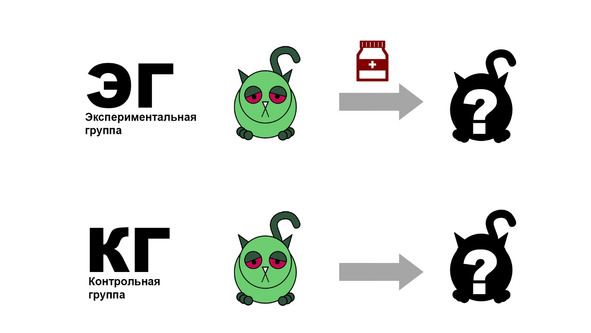
Каждую группу котиков мы замеряем по два раза: до приема и после приема лекарств. Итого мы получаем четыре замера, которые мы сравниваем между собой с помощью мер различий.

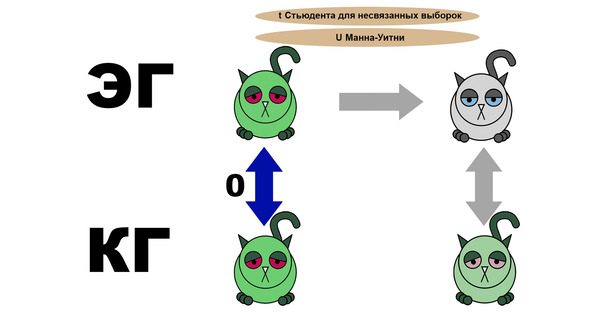
Первое, что мы должны сделать, это сравнить группы до эксперимента. Для этого используются t-критерий Стьюдента для несвязанных выборок или U-критерий Манна-Уитни. Котики при этом не должны различаться. Если в одной из групп котики более здоровы, то это очень плохо, поскольку не позволит четко отследить влияние лекарства.

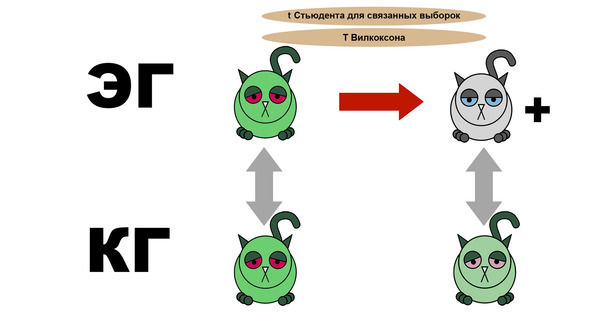
Далее мы сравниваем экспериментальную группу до и после приема лекарств с помощью t Стьюдента для связанных выборок либо T Викоксона. Если различия есть и состояние котиков улучшилось, то мы можем начинать радоваться. Но не сильно. Ведь вполне возможно, что контрольная группа продемонстрировала тот же результат.

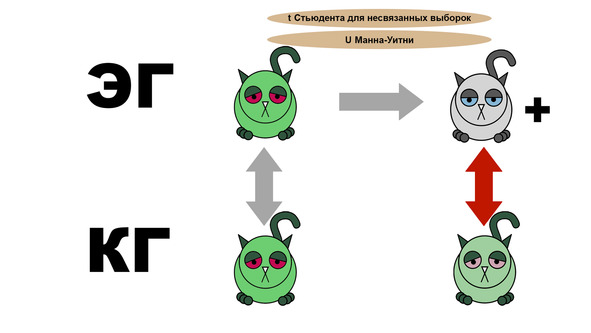
Поэтому последним замером мы смотрим, чем отличаются экспериментальная и контрольная группы после приема лекарств. Если различия есть, и экспериментальным котикам гораздо лучше, чем контрольным, то лекарство реально подействовало.

Таким образом, мы можем сделать вывод, что лекарство действует, только если до эксперимента между группами различий нет, после — есть и имеются положительные изменения состояния в экспериментальной и контрольной группах. Прочие варианты указывают либо на неэффективность лекарства, либо на неправильную организацию эксперимента.

Важно отметить следующее: поскольку для проверки эффективности лекарства мы вычисляли три критерия, то здесь возникает проблема множественных сравнений. Чтобы ее преодолеть, необходимо применить поправку Бонферрони и сравнивать p-уровень значимости не с 0,05, а с 0,017. В противном случае вы рискуете очень сильно ошибиться в своих выводах.

Альтернатива этому — использование дисперсионного анализа для повторных измерений, о котором будет рассказано в следующей главе.

Оглавление книги