Книга: Статистика и котики

Глава 12. Котиковые аналоги или основы математического моделирования

Глава 12.

Котиковые аналоги

или основы математического моделирования

В предыдущих разделах мы подробно рассмотрели метод регрессионного анализа, который позволяет построить уравнение, описывающее, как различные вещи влияют на настроение котиков. Подобные уравнения входят в группу объектов, называющихся математическими моделями.

Математическая модель — это своего рода аналог котика, который позволяет изучать его поведение без проведения реальных экспериментов. Как правило, это значительно удешевляет исследования.

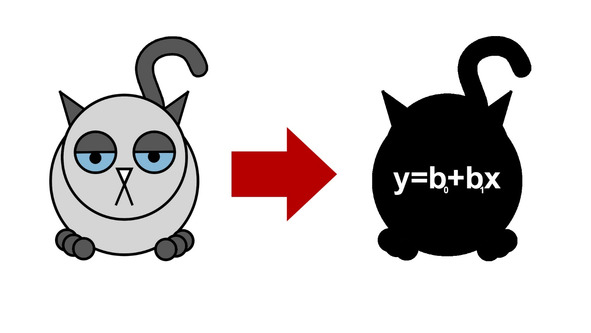
Все математические модели делятся на функциональные и структурные. Функциональные модели, к которым, к слову, относится регрессионное уравнение, — описывают влияние внешних факторов на котиковое состояние. Например, известная нам модель котикового счастья.

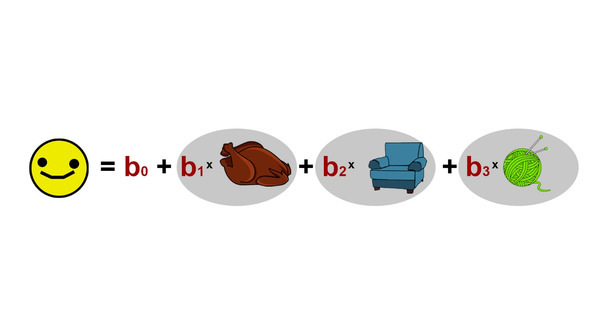
Особенность такой модели в том, что мы подробно не рассматриваем состав этого счастья. Счастье для нас — некий целостный объект, целевая переменная, которая может меняться: прибывать или убывать. А вот структурные модели позволяют описать его компоненты: от удовлетворения базовых котиковых потребностей до котиковой самореализации.

Как правило, функциональные модели записываются с помощью уравнений. А вот структурные могут быть достаточно разнообразными: от таблиц до блок-схем.

Любая математическая модель строится в два этапа. На первом этапе мы прикидываем, какие факторы в принципе могут влиять на котиковое счастье или из каких компонентов оно может состоять. Этот этап называется также построением содержательной модели.

Второй этап включает в себя сбор реальных данных и их математическую обработку. Он называется построением формальной модели. Формальную модель уже можно использовать как аналог реального котика. Изменяя различные параметры этой модели, вы сможете понять, как функционирует котик, не прибегая к опытам над животными.

НЕМАЛОВАЖНО ЗНАТЬ!

Классификация математических моделей

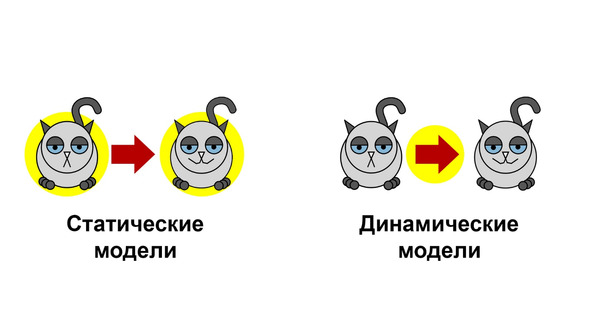
Помимо деления на функциональные и структурные модели есть еще несколько классификаций, о которых полезно знать. В частности бывают модели статические и динамические. Первые описывают состояние котика в какой-то конкретный момент. Вторые же концентрируются непосредственно на изменениях, которые претерпевает котик.

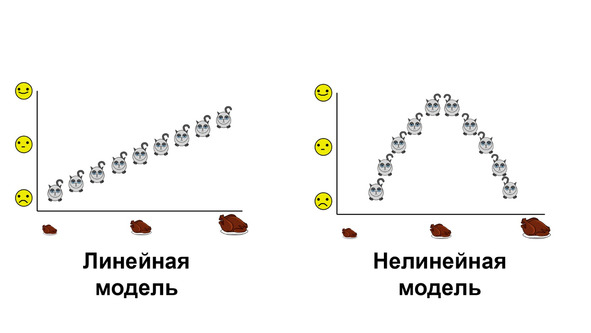
Кроме того, модели делятся на линейные и нелинейные. Линейные модели включают в себя только линейные взаимосвязи, о которых мы подробно говорили в главах про корреляционный и регрессионный анализы. Нелинейные модели могут включать в себя нелинейные взаимосвязи. Примером здесь может служить полиномиальная регрессия.

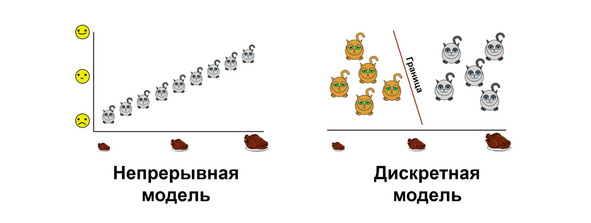
Также имеет смысл рассмотреть деление моделей на непрерывные и дискретные. Первые отличаются тем, что в них все переменные имеют бесконечное множество значений. Пример такой переменной — это котиковый размер, измеренный в сантиметрах. Мы можем сказать, что наш котик имеет длину 62 см. А можем — что 62,513987 см. И даже точнее. Если состояние вашего котика измеряется такой переменной, то, чтобы построить функциональную модель, вам необходима линейная регрессия.

Дискретные же модели работают с переменными, которые имеют ограниченное количество значений. Например, тот же размер, но имеющий только три значения: маленький, средний и большой. Построить модели с дискретными целевыми переменными, в частности, позволяют логистическая регрессия и дискриминантный анализ.

Впрочем, на практике большинство моделей относятся к смешанным типам — в них встречаются как дискретные, так и непрерывные переменные, а линейные взаимосвязи вполне могут сочетаться с нелинейными.

Оглавление книги