Книга: Говори на языке диаграмм: пособие по визуальным коммуникациям

4. Частотное сравнение

4. Частотное сравнение

Частотное сравнение показывает, сколько значений данного параметра (частотность) попадает в последовательные области числовых значений.

Этот тип сравнения применяется в двух основных случаях. Во-первых, для обобщения сходных событий на основе выборки наблюдений. Здесь частотное сравнение используется для того, чтобы предсказывать риск, вероятность или возможность. К примеру, посредством данного вида сравнения можно показать, что в 25 % случаев грузы доставляются за пять или менее дней, или выразить в процентах некую возможность – скажем, выбросить несчастливую семерку при игре в кости (берегите свои деньги: подобное происходит в каждом шестом случае).

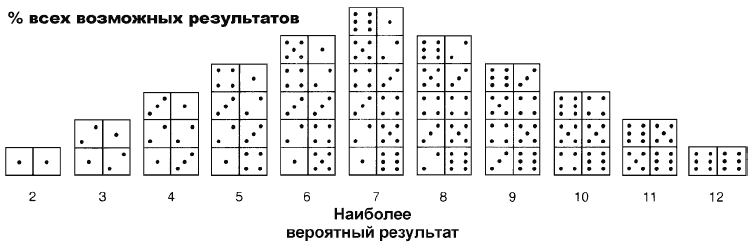
Колоколообразные кривые и многоугольники, связанные с применением частотного распределения, подчиняются математическим правилам. Облегчите себе жизнь и доверьте их подготовку профессиональному статистику. Поскольку эти кривые используются преимущественно в аналитических целях, мы не будем касаться их в этой книге.

Второй случай использования этого типа сравнения, нередко встречающийся в презентациях и докладах, – суммирование больших объемов информации для того, чтобы продемонстрировать значимую взаимосвязь (например, 25 % грузов доставляются за 5–6 дней). Подобное применение особенно полезно для отражения демографической информации – количества работников с определенным размером заработной платы, распределения семей по уровням дохода или модели голосования по возрастным группам. Неудивительно, что такой тип сравнения данных особенно часто используется во время переписи населения или президентских выборов.

ГИСТОГРАММА

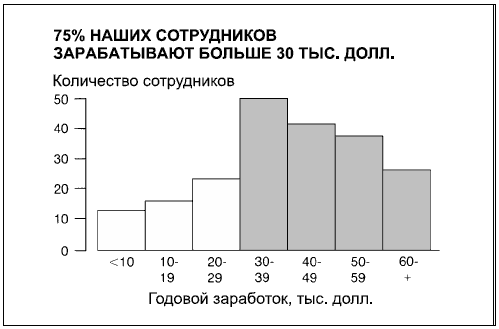
В вышеназванных целях данный тип сравнения лучше всего иллюстрировать с помощью ступенчатых гистограмм или графиков. Гистограммы нагляднее, когда используется не больше 5–7 областей числовых значений, в противном случае удобнее будет график.

ГРАФИК

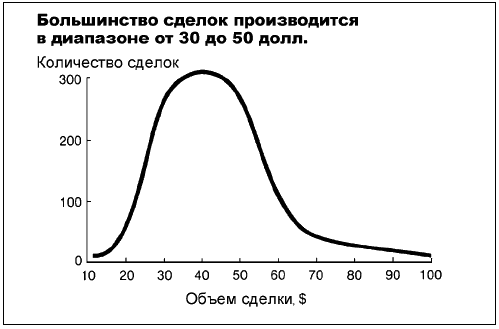
Эти типы диаграмм содержат две шкалы: вертикальную (частотности), где указывается количество (иногда в процентах) анализируемых элементов или явлений, и горизонтальную (распределения) для диапазонов. Шкала распределения требует особого внимания.

Размер диапазонов. Размер и количество диапазонов весьма важны для демонстрации модели распределения. Слишком малое количество не позволяет проследить модель, а слишком большое – разбивает ее на мелкие части. Как правило, применяется не менее пяти, но не более двадцати областей числовых значений. При этом размеры диапазонов должны нагляднее всего демонстрировать вашу основную мысль. Обратимся к конкретному примеру. Допустим, мы хотим создать модель распределения среднегодовых заработков учителей государственных школ в пятидесяти штатах.

При использовании диапазона в 500 долл. проследить зависимость не удается.

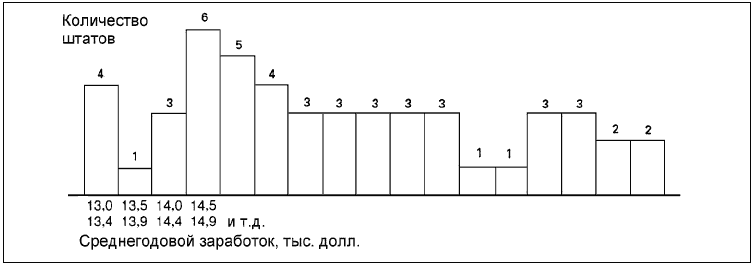
Если мы увеличим размер диапазона до 1 тыс. долл., модель начинает вырисовываться.

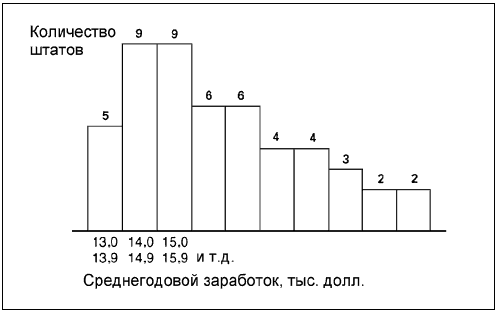
Но лишь при использовании дипазона в 2 тыс. долл. мы получаем наглядную модель. Здесь мы ясно видим колоко-лообразную кривую, которая обычно изображает частотное распределение. Кривая сдвинута влево, то есть к низшей стороне распределения. Это иллюстрирует основную идею: почти в половине штатов (в 23 из 50) учителям платят менее 16 тыс. долл. в год.

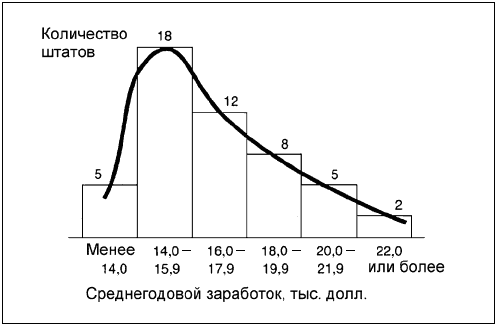
Размер интервалов. Лучше всего использовать интервалы одинакового размера. Если один интервал отражает разницу в 5 долл., а другой – в 20, кривая распределения получится искаженной. Исключением из этого правила являются случаи, когда информация фиксируется в неравных диапазонах (например, уровни образования) или когда неравные интервалы помогают лучше усвоить информацию (как в случае с разбросом подоходного налога). Разброс доходов настолько велик, что близко к низшей точке оказывается слишком много людей, а к высшей – слишком мало. Поэтому равные интервалы здесь применять нельзя. При использовании интервалов по 1 тыс. долл. придется чертить диаграмму в несколько метров шириной, а при интервалах по 40 тыс. долл. практически все население окажется в пределах первого интервала. Диаграмма будет наиболее информативной, если более мелкие интервалы использовать ближе к низшей точке, а более крупные – ближе к высшей.

Четкие границы. Размеры интервалов должны быть четко обозначены. «Перекрывающиеся» границы (0—10, 10–20, 20–30) не объясняют, к каким интервалам относятся цифры, повторяющиеся по два раза (10, 20). Для непрерывных величин (например, объемов продаж в долларах) предпочтительнее всего следующие границы – менее 10,00 долл., 10,00–19,99 долл., 20,00–29,99 долл. и т. д. Для дискретных величин (количество произведенных автомобилей и т. п.) – менее 10, 10–19, 20–29 и т. д.

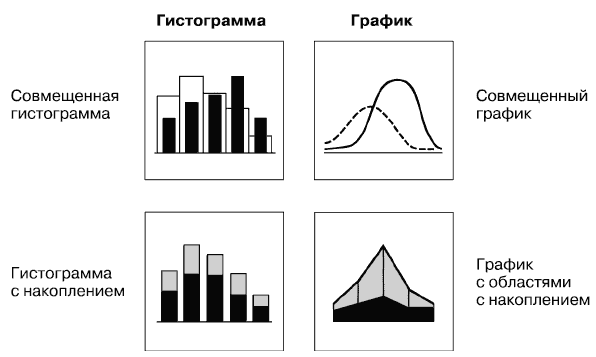
И гистограммы, и графики можно совмещать. Например, для того, чтобы сравнить данные по двум разным годам или сопоставить возрастной состав сотрудников вашей компании и компаний-конкурентов или в отрасли в целом. Кроме того, при иллюстрации конкретных величин можно применять диаграммы с накоплением, чтобы показать вклад каждого параметра в общую сумму[Внимание! Нельзя применять диаграммы с накоплением, когда частота распределения выражена в процентах. Например, если от 5 до 10 долл. в час зарабатывают 60 % женщин и 50 % мужчин, нельзя сказать, что в целом 110 % населения зарабатывают от 5 до 10 долл. в час.].

Оглавление книги