Книга: Программирование на языке Пролог для искусственного интеллекта

4.5.3. Программа 3

4.5.3. Программа 3

Наша третья программа для задачи о восьми ферзях опирается на следующие соображения. Каждый ферзь должен быть размещен на некотором поле, т.е. на некоторой вертикали, некоторой горизонтали, а также на пересечении каких-нибудь двух диагоналей. Для того, чтобы была обеспечена безопасность каждого ферзя, все они должны располагаться в разных вертикалях, разных горизонталях и в разных диагоналях (как идущих сверху вниз, так и идущих снизу вверх). Естественно поэтому рассмотреть более богатую систему представления с четырьмя координатами:

 x вертикали

 у горизонтали

 u диагонали, идущие снизу вверх

 v диагонали, идущие сверху вниз

Эти координаты не являются независимыми: при заданных x и у, u и v определяются однозначно (пример на рис. 4.10). Например,

u = x - у

v = x + у

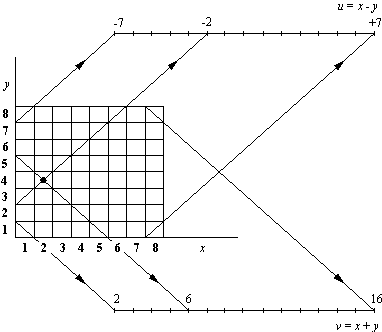
Рис. 4.10. Связь между вертикалями, горизонталями и диагоналями. Помеченное поле имеет следующие координаты: x = 2,  у = 4, u = 2 - 4 = -2, v = 2 + 4 = 6.

Области изменения всех четырех координат таковы:

Dx = [1, 2, 3, 4, 5, 6, 7, 8]
Dy = [1, 2, 3, 4, 5, 6, 7, 8]
Du = [-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7]
Dv = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]

Задачу о восьми ферзях теперь можно сформулировать следующим образом: выбрать восемь четверок (X, Y, U, V), входящих в области изменения (X в Dx, Y в Dy и т.д.), так, чтобы ни один их элемент не выбирался дважды из одной области. Разумеется, выбор X и Y определяет выбор U и V. Решение при такой постановке задачи может быть вкратце таким: при заданных 4-x областях изменения выбрать позицию для первого ферзя, вычеркнуть соответствующие элементы из 4-x областей изменения, а затем использовать оставшиеся элементы этих областей для размещения остальных ферзей. Программа, основанная на таком подходе, показана на рис. 4.11. Позиция на доске снова представляется списком Y-координат. Ключевым отношением в этой программе является отношение

peш( СписY, Dx, Dy, Du, Dv)

которое конкретизирует Y-координаты (в СписY) ферзей, считая, что они размещены в последовательных вертикалях, взятых из Dx. Все Y-координаты и соответствующие координаты U и V берутся из списков Dy, Du и Dv. Главную процедуру решение можно запустить вопросом

?-  решение( S)

Это вызовет запуск реш с полными областями изменения координат, что соответствует пространству задачи о восьми ферзях.

решение( СписY) :-
 реш( СписY, % Y-координаты ферзей
 [1, 2, 3, 4, 5, 6, 7, 8],
  % Область изменения Y-координат
 [1, 2, 3, 4, 5, 6, 7, 8],
  % Область изменения X-координат
 [-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7],
  % Диагонали, идущие снизу вверх
 [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 14, 15, 16] ).
  % Диагонали, идущие сверху вниз
реш([], [], Dy, Du, Dv).
реш( [Y | СписY], [X | Dx1], Dy, Du, Dv) :-
 удалить( Y, Dy, Dy1), % Выбор Y-координаты
 U is X-Y,             % Соответствующая диагональ вверх
 удалить( U, Du, Du1), % Ее удаление
 V is X+Y,             % Соответствующая диагональ вниз
 удалить( V, Dv, Dv1), % Ее удаление
 реш( СписY, Dх1, Dy1, Du1, Dv1).
  % Выбор из оставшихся значений
удалить( А, [А | Список], Список).
удалить(A, [В | Список ], [В | Список1 ] ) :-
 удалить( А, Список, Список1).

Рис. 4.11. Программа 3 для задачи о восьми ферзях.

Процедура реш универсальна в том смысле, что ее можно использовать для решения задачи об N ферзях (на доске размером N?N). Нужно только правильно задеть области Dx, Dy и т.д.

Удобно автоматизировать получение этих областей. Для этого нам потребуется процедура

генератор( N1, N2, Список)

которая для двух заданных целых чисел N1 и N2 порождает список

Список = [N1, N1 + 1, N1 + 2, ..., N2 - 1, N2]

Вот она:

генератор( N, N, [N]).
генератор( Nl, N2, [Nl | Список]) :-
 N1 < N2,
 М is N1 + 1,
 генератор( М, N2, Список).

Главную процедуру решение нужно соответствующим образом обобщить:

решение( N, S)

где N — это размер доски, а S — решение, представляемое в виде списка Y-координат N ферзей. Вот обобщенное отношение решение:

решение( N, S) :-
 генератор( 1, N, Dxy),
 Nu1 is 1 - N, Nu2 is N - 1,
 генератор( Nu1, Nu2, Du),
 Nv2 is N + N,
 генератор( 2, Nv2, Dv),
 реш( S, Dxy, Dxy, Du, Dv).

Например, решение задачи о 12 ферзях будет получено с помощью:

?-  решение( 12, S).
S = [1, 3, 5, 8, 10, 12, 6, 11, 2, 7, 9, 4]

Оглавление книги