Книга: Программирование на языке Пролог для искусственного интеллекта

10.2. AVL-дерево: приближенно сбалансированное дерево

10.2. AVL-дерево: приближенно сбалансированное дерево

AVL-дерево — это дерево, обладающее следующими свойствами:

(1) Левое и правое поддеревья отличаются по глубине не более чем на 1.

(2) Оба поддерева являются AVL-деревьями.

Деревья, удовлетворяющие этому определению, могут быть слегка разбалансированными. Однако можно показать, что даже в худшем случае глубина AVL-дерева примерно пропорциональна log n, где n — число вершин дерева. Таким образом гарантируется логарифмический порядок производительности операций внутри, добавить и удалить.

Операции над AVL-деревом работают по существу так же, как и над двоичным справочником. В них только сделаны добавления, связанные с поддержанием приближенной сбалансированности дерева. Если после вставления или удаления дерево перестает быть приближенно сбалансированным, то специальные механизмы возвращают ему требуемую степень сбалансированности. Для того, чтобы эффективно реализовать этот механизм, нам придется сохранять некоторую дополнительную информацию относительно степени сбалансированности дерева. На самом деле, нам нужно знать только разность между глубинами поддеревьев, которая может принимать значения -1, 0 или +1. Тем не менее для простоты мы предпочтем сохранять сами величины глубин поддеревьев, а не разности между ними.

Мы определим отношение вставления элемента как

доб_avl( Дер, X, НовДер)

где оба дерева Дер и НовДер — это AVL-деревья, причем НовДер получено из Дер вставлением элемента X. AVL-деревья будем представлять как термы вида

д( Лев, А, Прав)/Глуб

где А — корень, Лев и Прав — поддеревья, а Глуб — глубина дерева. Пустое дерево изображается как nil/0. Теперь рассмотрим вставление элемента X в непустой AVL-справочник

Дер = д( L, A, R)/H

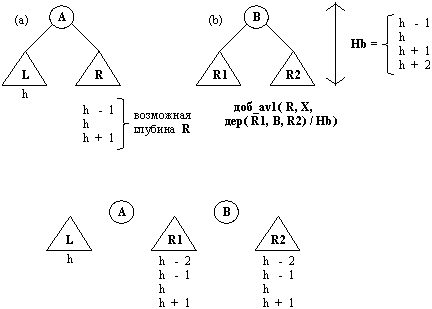
Рис. 10.8. Задача вставления элемента в AVL-справочник (a) AVL-дерево перед вставлением X, X > А; (b) AVL-дерево после вставления X в R; (с) составные части, из которых следует построить новое дерево.

Начнем со случая, когда X больше А. X необходимо вставить в R, поэтому имеем следующее отношение:

доб_аv1( R, X, д( R1, В, R2)/Hb)

На рис. 10.8 показаны составные части, из которых строится дерево НовДер:

L, А, R1, В, R2

Какова глубина деревьев L, R, R1 и R2?  L и R могут отличаться по глубине не более, чем на 1. На рис. 10.8 видно, какую глубину могут иметь R1 и R2. Поскольку в R был добавлен только один элемент X, только одно из поддеревьев R1, R2 может иметь глубину h+1.

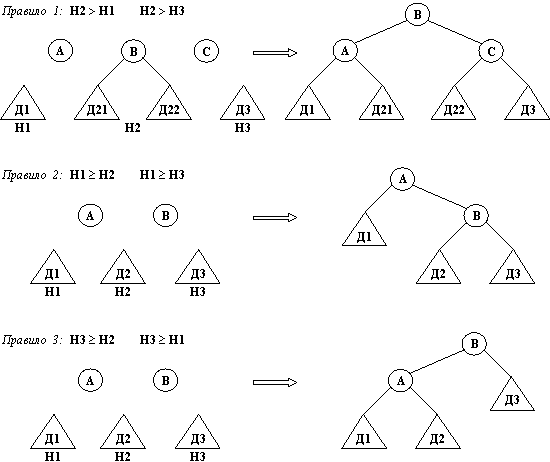
Рис. 10.9. Три правила построения нового AVL-дepевa.

В случае, когда X меньше, чем А, имеем аналогичную ситуацию, причем левое и правое поддеревья меняются местами. Таким образом, в любом случае мы должны построить дерево НовДер, используя три дерева (назовем их Дер1, Дер2 и Дер3) и два отдельных элемента А и В. Теперь рассмотрим вопрос: как соединить между собой эти пять составных частей, чтобы дерево НовДер было AVL-справочником? Ясно, что они должны располагаться внутри НовДер в следующем порядке (слева направо):

Дер1, А, Дер2, В, Дер3

Рассмотрим три случая:

(1) Среднее дерево Дер2 глубже остальных двух деревьев.

(2) Дер1 имеет глубину не меньше, чем Дер2 и Дер3.

(3) Дер3 имеет глубину не меньше, чем Дер2 и Дер1.

На рис. 10.9 видно, как можно построить дерево НовДер в каждом из этих трех случаев. Например, в случае 1 среднее дерево Дер2 следует разбить на два части, а затем включить их в состав НовДер. Три правила, показанные на pис.10.9, нетрудно запасать на Прологе в виде отношения

соединить( Дер, А, Дер2, В, Дер3, НовДер)

Последний аргумент НовДер — это AVL-дерево, построенное из пяти составных частей, пяти первых аргументов. Правило 1, например, принимает вид:

соединить( Д1/Н1, А, д( Д21, В, Д22)/Н2, С, Д3/Н3,
  % Пять частей
 д( д( Д1/Н1, А, Д21)/На, В, д( Д22, С, Д3/Н3)/Нс)/Нb) :-
  % Результат
 H2 > H1, H2 > Н3, % Среднее дерево глубже остальных
 На is Н1 + 1,     % Глубина левого поддерева
 Нс is Н3 + 1,     % Глубина правого поддерева
 Hb is На + 1,     % Глубина всего дерева

Программа доб_аvl, вычисляющая также глубину дерева и его поддеревьев, показана полностью на рис. 10.10.

10.3. Определите отношение

avl( Дер)

для проверки того, является ли Дер AVL-деревом, т.е. верно ли, что любые два его поддерева, подсоединенные к одной и той же вершине, отличаются по глубине не более чем на 1. Двоичные деревья представляйте в виде термов д( Лев, Кор, Прав) или nil.

% Вставление элемента в AVL-справочник
доб_аvl( nil/0, X, д( nil/0, X, nil/0)/1).
  % Добавить X к пустому дереву
доб_аvl( д( L, Y, R)/Ну, X, НовДер) :-
  % Добавить X к непустому дереву
 больше( Y, X),
 доб_аvl( L, X, д( L1, Z, L2)/ _ ),
  % Добавить к левому поддереву
 соединить( L1, Z, L2, Y, R, НовДер).
  % Сформировать новое дерево
доб_avl( д( L, Y, R)/Ну, X, НовДер) :-
 больше( X, Y),
 доб_avl( R, X, д( R1, Z, R2)/ _ ),
  % Добавить к правому поддереву
 соединить( L1, Y, Rl, Z, R2, НовДер).
соединить( Д1/Н1, А, д( Д21, В, Д22)/Н2, С, Д3/Н3,
 д( д( Д1/Н1, А, Д21)/На, В, д( Д22, С, L3/Н3)/Нс)/Нb) :-
 Н2 > H1, H2 > Н3,     % Среднее дерево глубже остальных
 На is H1 + 1,
 Hс is Н3 + 1,
 Нb is На + 1.
соединить( Д1/Н1, А, д( Д2/Н2, С, Д3/Н3,
 д( Д1/Н1, А, д( Д2/Н2, С, Д3/Н3)/Нс)/На) :-
 H1 >= H2, H1 >= Н3,   % "Глубокое" левое дерево
 max1( H2, Н3, Нс),
 max1( H1, Нс, На).
соединить( Д1/Н1, А, Д2/Н2, С, Д3/Н3,
 д( д( Д1/Н1, А, Д2/Н2)/На, С, Д3/Н3)/Нс) :-
 Н3 >= H2, Н3 >= H1,   % "Глубокое" правое дерево
 max1( H1, H2, На),
 max1( На, Н3, Нс).
max1( U, V, М) :-
 U > V, !, М is U + 1; % М равно 1 плюс max( U, V)
 М is V + 1.

Рис. 10.10. Вставление элемента в AVL-справочник. В этой программе предусмотрено, что попытка повторного вставления элемента терпит неудачу. По поводу процедуры соединить см. рис. 10.9.

Оглавление книги