Книга: Технологии программирования
5.9. МЕТОДИКА РАЗРАБОТКИ АЛГОРИТМОВ ПРОГРАММ
5.9. МЕТОДИКА РАЗРАБОТКИ АЛГОРИТМОВ ПРОГРАММ
Рассмотрим порядок работы по методике разработки структурированных алгоритмов на следующем примере. Пусть требуется разработать программу решения квадратного уравнения, которое имеет вид
ax2 + bx + c = 0.
Работа по методике начинается с полного уяснения задачи. Этому помогает применение модели "черного ящика", разработка форм вводимой и выводимой информации программы (например, в виде макетов экрана), подготовка первичных тестовых примеров. Не существует для всего многообразия задач точный порядок выполнения этих действий. Данные действия часто приходится выполнять параллельно, переключаясь с действия на действие по мере исчерпания возможностей развития текущего действия и открытия возможностей развития очередного действия.
Первоначально алгоритм должен представлять одну типовую структуру СЛЕДОВАНИЕ (одно действие со смыслом выполнить все действия программы, например, программа начисления заработанной платы, но не программа начисления заработанной платы и/или решения квадратного уравнения).
Глядя на тесты и изображение модели "черного ящика" (см. рис. 5.3), детализируем весь алгоритм как одно СЛЕДОВАНИЕ (последовательно выполняемое действие) в порядке: а) предварительная запись смысла действия "черного ящика"; б) выходная и/или выводимая информация; в) входная и/или вводимая информация; г) определяется действие в "черном ящике" (одно предложение).
При разработке алгоритмов программ входная, промежуточная и выходная информации характеризуются структурой данных. Важным являются порядок размещения значений в массивах, имена и значения констант описания размерностей массива, имена и значения переменных, характеризующие текущие значения используемого размера массива, имя и порядок изменения переменной индекса текущего элемента массива. Форма вводимой и выводимой на экран или печать информации может быть показана макетами экранов или документов.
Первичные тестовые примеры должны включать как обычные, так и стрессовые наборы тестовых входных данных. Каждый стрессовый набор тестовых данных предназначен для выявления реакции в особых случаях. Например: неверных действий пользователя, деления на ноль, выхода значения за допустимые границы и т. д. Любой набор тестовых данных должен содержать описание результата.
Исследуя "черный ящик" применительно к решению квадратного уравнения, можем записать предварительный комментарий сути всех действий программы: "Программа решения квадратного уравнения вида a*x*x + b*x + c = 0".
Далее выясняется, что еще не выявлена выходная информация "черного ящика", поэтому необходимо перейти к подготовке тестов, что поможет продолжить работу с "черным ящиком". В данном конкретном случае подготовить тесты поможет анализ задачи.
Итак, пусть известна "школьная" формула решения квадратного уравнения вида ax2 + bx + с = 0.
Известно также, что первоначально надо вычислить дискриминант уравнения D:
D = b2 — 4ac.
Даже если забыли о случае отрицательности дискриминанта — ничего страшного нет. Записываем формулу решения:
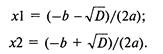
Нам известно, что если D < 0, то из отрицательного числа нельзя извлекать квадратный корень. Поэтому вспоминаем, что при отрицательном дискриминанте нет корней. Еще обнаруживаем факт особого случая, которому соответствует факт при D = 0 наличия двух равных корней. Еще известно, что делить на ноль нельзя, а при a = 0 имеем именно этот случай. В этом случае исходное квадратное уравнение превращается в линейное уравнение:
bx + c = 0.
Решение получившегося уравнения будет следующим:
x = (—c)/b.
Это решение возможно лишь в случае a = 0 и (одновременно) b ? 0. В случае a = 0 и (одновременно) b = 0 и (одновременно) c ? 0 линейное уравнение не имеет решения.
Анализируя исходное уравнение, выясняем, что в случае a = 0 и (одновременно) b = 0 и (одновременно) c = 0 уравнение имеет бесчисленное множество решений (корни x1 и x2 — любые числа).
Составим наглядную таблицу правил решения квадратного уравнения (табл. 5.3).
Таблица 5.3
Наглядная таблица правил решения квадратного уравнения
| № п/п | а | b | с | d | Вариант решения |
| 1 | a ? 0 | Любое | Любое | d > 0 | Два различных корня |
| 2 | a ? 0 | Любое | Любое | d = 0 | Два равных корня |
| 3 | a ? 0 | Любое | Любое | d < 0 | Нет решения |
| 4 | а = 0 | b ? 0 | Любое | Нет | Есть корень линейного уравнения |
| 5 | а = 0 | b = 0 | c ? 0 | Нет | Нет решения |
| 6 | а = 0 | b = 0 | с = 0 | Нет | Бесчисленное множество решений |
В табл. 5.3 нет сочетаний значений, которые еще не выявлены. Теперь можно определить выходную информацию "черного ящика", которая выдается в пяти вариантах:
1) уравнение имеет бесчисленное множество решений (корни x1 и x2 — любые числа);
2) значения двух различных корней x1 и x2;
3) значения двух равных корней в виде x1 и дополняющей надписи о двух равных корнях;
4) надпись нет решения;
5) значение одного корня x1 с надписью, что уравнение является линейным.
Тип переменных, в которых размещаются выходные значения корней x1 и x2, — вещественный (Real). Теперь определяем входную информацию. Из исходного уравнения следует, что входной информацией являются значения трех коэффициентов a, b, c типа вещественный (Real). В ходе анализа формул было установлено, что значения трех коэффициентов a, b, c могут принимать любые значения, что было не очевидно до анализа формул решения уравнения (например, случай a = 0).
Имена переменных будут достаточно мнемоничны, если придерживаться принятых в математике обозначений.
Окончательный комментарий сути действий всей программы: "Программа решения квадратного уравнения a*x*x + b*x + c = 0 с произвольными значениями коэффициентов a, b, c типа вещественный". Факт произвольности значений коэффициентов a, b, c на этапе предварительного выявления сути действия "черного ящика" еще не был выявлен.
Наконец, готовим тестовые примеры.
Совокупность тестов для всех выявленных случаев решения квадратного уравнения:
1) при a = 0, b = 0, c = 0 бесчисленное множество решений (корни x1 и x2 — любые числа);
2) при a = 2, b = 3, c = —2 значения двух различных корней x1 = —2 и x2 = 0,5;
3) при a = 1, b = 4, c = 4 значения двух равных корней в виде x1 = x2 = —2 и вывод дополняющей надписи о двух равных корнях;
4) при а = 2, b = 5, с = 4 вывод надписи "нет решения";
5) при a = 0, b = 2, c = —8 значение одного корня x1 = 4 с надписью, что уравнение является линейным;
6) при a = 0, b = 0, c = 2 вывод надписи "нет решения". Теперь можно сразу написать фрагмент программы, соответствующий проделанной работе:
Program Kvadrat;
{ Программа решения квадратного уравнения
вида a*x*x + b*x + c = 0 с произвольными
значениями коэффициентов a, b, c типа
вещественный }
Uses
Crt, Dos;
Var
a, b, c: Real; {Коэффициенты квадратного уравнения}
xl, x2: Real; {Корни квадратного уравнения}
begin
end.
Путем компиляции фрагмента программы на компьютере можно проверить корректность синтаксиса. Теперь подготовим макет изображения экрана монитора (рис. 5.16). На макете изображения экрана монитора символами ? отмечены поля ввода информации, а символами — поля вывода информации.
Обычно выводимая на экран информация не содержит имен переменных, но в данном случае принятые в математике имена целесообразно отобразить на экране.
Макет изображения экрана монитора также является тестом. На основе первичных тестовых примеров и организации входной и выходной информации готовится или один тест, или несколько обобщающих тестов. Все составленные тесты для решения квадратного уравнения вошли в обобщающий тест.
Разработка наглядных тестов. Для простейшего алгоритма решения квадратного уравнения первичные тесты вместе с математическими формулами уже обладают наглядностью. Продолжим составление программы решения квадратного уравнения.
Первоначально нужно выполнить действия, определенные макетом изображения на экране монитора, так как для выполнения алгоритма решения квадратного уравнения необходимы исходные данные в виде коэффициентов a, b, c. Однако вводу должен предшествовать вывод информации, поясняющей назначение программы и суть очередной вводимой порции данных. Это предопределяет первичную детализацию одиночное СЛЕДОВАНИЕ в ЦЕПОЧКУ СЛЕДОВАНИЙ. Первичное одиночное СЛЕДОВАНИЕ не может содержать входной и выходной информации. Входная информация должна либо быть введена, либо присвоена. Выходная информация по завершении программы никого не интересует. Итак, ниже представлена цепочка последовательных действий.

Рис. 5.16. Макет изображения экрана монитора
ClrScr; {Очистка экрана}
{Вывод информации о назначении программы}
WriteLn ('Программа решения квадратного уравнения');
WriteLn ('вида а*x*x + b*x + с = 0 с произвольны','ми значениями');
WriteLn ('коэффициентов a, b, c типа вещественный');
WriteLn;
{Ввод значений коэффициентов a, b, c}
Write ('Укажите значение коэффициента а = ');
ReadLn (a); {Ввод а}
Write ('Укажите значение коэффициента b = ');
ReadLn (b); {Ввод b}
Write ('Укажите значение коэффициента с = ');
ReadLn (с); {Ввод с}
{ Вывод проверочно-протокольной информации о введенных значениях коэффициентов a, b, c}
WriteLn;
WriteLn ('Решается квадратное уравнение');
WriteLn (а:10:4, '*x*x + ', b:10:4, '* x + ', с:10:4, ' = 0:'); { Само решение квадратного уравнения }
WriteLn;
Write ('Для завершения программы нажмите');
WriteLn (' любую клавишу…');
Repeat until KeyPressed; { Цикл ожидания нажатия любой клавиши }
Действие "Очистка экрана" — артефакт реализации, а не задачи, но насколько приятнее обозревать экран без "лишней информации". Также артефактом реализации явились два последних оператора, которые обеспечивают удобство просмотра результатов работы программы. При отсутствии этих операторов и нахождении в оболочке Turbo Pascal для просмотра результатов работы программы пришлось бы вручную переключиться в окно результатов.
Написание операторов WriteLn, Write, ReadLn не вызвало затруднений благодаря заранее подготовленному макету изображения экрана монитора.
Действие "Само решение квадратного уравнения" представлено комментарием и пустой строкой, отмечающей факт добавления действий в будущем. Это объясняется тем, что решение и вывод результатов решения многовариантны, а, следовательно, действие "Само решение квадратного уравнения" нельзя представить ЦЕПОЧКОЙ СЛЕДОВАНИЙ. Многовариантность предполагает управляющие структуры.
Уточняем комментарии, операторы вывода Write и WriteLn.
Проводим проверку информационной согласованности СЛЕДОВАНИЙ в цепочке. Убеждаемся, что все последующие действия обеспечены информацией, определенной предшествующими действиями, в конкретном случае — операторами ReadLn. Особое внимание обращаем на действия, использующие ранее определенную информацию. Это оператор
WriteLn (a:10:4, '*x*x + ', b:10:4, '*x + ', c: 10:4, ' = 0: ');
и будущее действие
{ Само решение квадратного уравнения }.
Убеждаемся, что к моменту их выполнения значения коэффициентов a, b, c уже определены. Теперь можно собрать реализованную часть программы и путем ее выполнения на тестах убедиться, что действия ввода и вывода введенной информации программы исполняются корректно.
Program Kvadrat;
{ Программа решения квадратного уравнения
вида а*х*х + Ь*х + с = 0 с произвольными значениями
коэффициентов а, Ь, с типа вещественный }
Uses
Crt, Dos;
Var
a, b, c: Real; {Коэффициенты квадратного уравнения}
xl, x2: Real; {Корни квадратного уравнения}
begin
ClrScr; {Очистка экрана}
{Вывод информации о значении программы}
WriteLn ('Программа решения квадратного уравнения');
Write ('вида а*х*х + b*х + с = 0 с произвольными');
Write ('значениями');
WriteLn ('коэффициентов а, b, с типа вещественный');
WriteLn
{Ввод значений коэффициентов a, b, c}
Write ('Укажите значение коэффициента а = ');
ReadLn (a); { Ввод а}
Write ('Укажите значение коэффициента b = ');
ReadLn (b); { Ввод b}
Write ('Укажите значение коэффициента с = ');
ReadLn (c); { Ввод с}
{ Вывод проверочно-протокольной информации о введенных значениях коэффициентов а, Ь, с }
WriteLn;
WriteLn ('Решается квадратное уравнение');
Write (a:10:4, '*x*x + ', b:10:4, '*x + ');
WriteLn (c:10:4, ' = 0: ');
{ Само решение квадратного уравнения }
WriteLn;
WriteLn ('Для завершения программы нажмите ', 'любую клавишу…');
repeat until KeyPressed; { Цикл ожидания нажатия любой клавиши}
end.
При сборке программы пришлось осуществить перенос части оператора WriteLn на новую строку.
Теперь осуществляем декомпозицию действия "Само решение квадратного уравнения".
Многовариантность вычислений предполагает цепочку альтернатив. Анализируя математические формулы обобщающего теста, табл. 5.3 и состав наборов выходной информации, выявляем, что ЦЕПОЧКА АЛЬТЕРНАТИВ содержит четыре альтернативных действия. Строкам с 1-й по 3-ю табл. 5.3 соответствует одно действие, поскольку для их выполнения требуется уже вычисленное значение дискриминанта d. Записываем комментарий предшествующего СЛЕДОВАНИЯ всей ЦЕПОЧКИ АЛЬТЕРНАТИВ, набор входной информации (выходной информации — нет) и оформляем заготовку операторов ЦЕПОЧКИ АЛЬТЕРНАТИВ вместе с подчиненными СЛЕДОВАНИЯМИ:
Входная информация: a, b, c
{ Само решение квадратного уравнения }
if
then
begin
{ Продолжение решения с вычислением дискриминанта }
end;
if
then
begin
{ Решение линейного уравнения }
end;
if
then
begin
{ Ввод сообщения: линейное уравнение не имеет решения }
WriteLn ("Нет решения ')
end;
if
then
begin
{ Вывод сообщения: бесчисленное множество решений уравнения }
Write ('бесчисленное множество решений уравне');
WriteLn ('ния (корни — любые числа)');
end;
В последней альтернативе одна строка выводится одним оператором.
Далее в соответствии с действиями запишем логические условия выполнения действий. При этом простым сравнением проверять на равенство значения двух вещественных переменных нельзя. Например, при сравнении f = g, считающихся равными 5, даже если g = 5,00000, в силу округлений при вычислениях значение f может оказаться равным либо 4,99999, либо 5,00000, либо 5,00001. Согласно данному примеру путем простой проверки на равенство факт равенства будет установлен в одном случае из трех.
Для надежного сравнения двух вещественных чисел используют прием использования неравенства |f — g| ? ?, где ? — заведомо малое число. На языке программирования это неравенство имеет вид
Abs (f — g) <= 1е — 6
Продолжаем кодирование структуры. Глядя на действия, записываем логические условия выполнения действий. Входная информация: a, b, c.
{ Само решение квадратного уравнения }
if (Abs(а) > 1e — 6)
then
begin
{ Продолжение решения с вычислением дискриминанта }
end;
if ((Abs (a) <= 1e — 6) and (Abs (b) > 1e — 6))
then
begin
{ Решение линейного уравнения }
end;
if ((Abs(a) <= 1e — 6) and (Abs(b) <= 1e — 6 and (Abs(c) > 1e — 6))
then
begin
{ Вывод сообщения: линейное уравнение не имеет решения }
WriteLn ('Нет решения');
end;
if ((Abs(a) <= 1e — 6) and (Abs(b) <= 1e — 6 and (Abs(c) <= 1e — 6))
then
begin
{ Вывод сообщения: бесчисленное множество решений уравнения }
Write ('бесчисленное множество решений уравне');
WriteLn ('ния (корни — любые числа)');
end;
Осуществим сборку получившейся программы. При сборке удалим избыточные комментарии и избыточные операторные скобки begin — end, охватывающие лишь один оператор. Испытаем полученную программу на тестах a = 0, b = 0, c = 0 a = 0, b = 0, c = 2. Собранный вариант программы:
Program Kvadrat;
{ Программа решения квадратного уравнения
вида a*x*x + b*x + c = 0 с произвольными значениями
коэффициентов a, b, c типа вещественный }
Uses
Crt, Dos;
Var
a, b, c: Real; {Коэффициенты квадратного уравнения}
xl, x2: Real; {Корни квадратного уравнения}
begin
ClrScr; { Очистка экрана }
{Вывод информации о назначении программы}
WriteLn ('Программа решения квадратного уравнения');
Write ('вида a*x*x + b*x + c = 0 с произвольными');
Write ('значениями');
WriteLn ('коэффициентов a, b, c типа вещественный');
WriteLn;
{Ввод значений коэффициентов а, b, с};
Write ('Укажите значение коэффициента а = ');
ReadLn(a); { Ввод а}
Write ('Укажите значение коэффициента b = ');
ReadLn(b); { Ввод b}
Write ('Укажите значение коэффициента с = ');
ReadLn(c); { Ввод с}
{ Вывод проверочно-протокольной информации
о введенных значениях коэффициентов a, b, c }
WriteLn;
WriteLn ('Решается квадратное уравнение');
Write (a:10:4, '*x*x + ', b:10:4, '*x + ');
WriteLn(с:10:4, ' = 0:');
{ Само решение квадратного уравнения }
if (Abs (a) > 1e — 6)
then
begin
{ Продолжение решения с вычислением дискриминанта }
end;
if ((Abs(a) <= 1e — 6) and (Abs(b) > 1e — 6))
then
begin
{ Решение линейного уравнения }
end;
if ((Abs(a) <= 1e — 6) and (Abs(b) <= 1e — 6) and (Abs(c) > 1e — 6))
then
WriteLn ('Нет решения');
if ((Abs(a) <= 1e — 6) and (Abs(b) <= 1e — 6 and (Abs(c) <= 1e — 6))
then
begin
Write ('бесчисленное множество решений уравне');
WriteLn ('ния (корни — любые числа)');
end;
WriteLn;
Write ('Для завершения программы нажмите');
WriteLn ('любую клавишу…');
repeat until KeyPressed; { Цикл ожидания нажатия любой клавиши }
end.
Декомпозируем действие "Решение линейного уравнения". Это действие представляет цепочку из двух элементарных операторов. Выполним проверку информационной согласованности действий:
Входная информация: b, с.
{ Решение линейного уравнения }
x1:= — c/b;
WriteLn ('уравнение линейное x = ', x1: 10: 4);
Декомпозируем действие "Продолжение решения с вычислением дискриминанта". Данное действие представляет ЦЕПОЧКУ СЛЕДОВАНИЙ из двух СЛЕДОВАНИЙ.
Входная информация: а, Ь, с
{ Продолжение решения с вычислением дискриминанта }
{ Вычисление дискриминанта квадратного уравнения }
d:= Sqr (b) — 4.0*а*с; { Решение уравнения }
Переменная d у нас не описана, поэтому в секцию Var необходимо добавить строку описания:
d: Real; { Значение дискриминанта }
Декомпозируем действие "Решение уравнения". Согласно табл. 5.3 данное действие представляет ЦЕПОЧКУ АЛЬТЕРНАТИВ из трех альтернатив в цепочке. Осуществив детализацию этих альтернатив в установленном порядке, получим:
Входная информация: a, b, c, d.
{ Решение уравнения }
if d > 1e-6
then
begin
{ Расчет двух различных корней }
end;
if ((d >= -1e-6) and (d <= 1e-6))
then
begin
{ Расчет двух равных корней }
WriteLn ('два равных корня x = ', (-b)/(2.0 * а):10:4);
end;
if d < -1e-6 then begin
{ Вывод надписи: уравнение не имеет решения }
WriteLn ('уравнение не имеет решения');
end;
Декомпозируем действие "Расчет двух различных корней". Это действие представляет цепочку из трех элементарных операторов. Выполним проверку информационной согласованности действий:
Входная информация: a, b, c, d
{ Расчет двух различных корней }
x1:= ((-b) — Sqrt (d))/(2.0*a);
x2:= ((-b) + Sqrt (d))/(2.0*а);
Write ('два различных корня x1 = ', x1:10:4);
WriteLn (' x2 = ', х2:10:4);
Здесь вывод одной строки осуществлен двумя операторами. Осуществим сборку всей программы, удалив избыточные комментарии и избыточные операторные скобки begin — end, охватывающие лишь один оператор. Испытаем полученную программу на всех заранее подготовленных тестах. Собранный вариант программы:
Program Kvadrat;
{ Программа решения квадратного уравнения
вида a*x*x + b*x + c = 0 с произвольными значениями
коэффициентов a, b, c типа вещественный }
Uses
Crt, Dos;
Var
a, b, c: Real; {Коэффициенты квадратного уравнения}
xl, x2: Real; {Корни квадратного уравнения}
dl: Real; {Значение дискриминанта}
begin
ClrScr; { Очистка экрана }
{Вывод информации о назначении программы}
WriteLn ('Программа решения квадратного уравнения');
WriteLn ('вида a*x*x + b*x + c = 0 с произвольными', 'значениями');
WriteLn ('коэффициентов a, b, c типа ', 'вещественный');
WriteLn
{Ввод значений коэффициентов a, b, c}
Write ('Укажите значение коэффициента а = ');
ReadLn(a); { Ввод а }
Write ('Укажите значение коэффициента b = ');
ReadLn(b); { Ввод b}
Write ('Укажите значение коэффициента с = ');
ReadLn(c); { Ввод с }
{ Вывод проверочно-протокольной информации
о введенных значениях коэффициентов a, b, c }
WriteLn;
WriteLn ('Решается квадратное уравнение');
WriteLn (а:10:4, '*x*x + ', b:10:4, '*x + ', с:10:4, ' = 0:');
{ Само решение квадратного уравнения }
if (Abs (a) > 1e-6)
then
begin
{ Продолжение решения с вычислением дискриминанта }
{ Вычисление дискриминанта квадратного уравнения }
d:= Sqr(b) — 4.0*а*с;
{ Решение уравнения }
if d > 1e-6
then
begin
{ Расчет двух различных корней }
x1:= (-b) — Sqrt(d)/(2.0*a);
х2:= (-b) + Sqrt(d)/(2.0*a);
Write ('два различных корня x1 = ', x1:10:4);
WriteLn (' х2 = ', х2:10:4);
end;
if ((d >= -1e-6) and (d <= 1e-6))
then
WriteLn ('два равных корня х = ', (-b)/(2.0*a):10:4);
if d < -1e-6 then
WriteLn ('уравнение не имеет решения');
end;
if ((Abs(a) <= 1e-6) and (Abs(b) > 1e-6))
then
begin
{ Решение линейного уравнения }
x1:= — c/b;
WriteLn ('уравнение линейное х = ', x1:10:4);
end;
if ((Abs(a) <= 1e-6) and (Abs(b) <= 1e-6 and (Abs(c) > 1e-6))
then
WriteLn ('Нет решения');
if ((Abs(a) <= 1e-6 and (Abs(b) <= 1e-6 and (Abs(c) <= 1e-6))
then
begin
Write ('Бесчисленное множество решений',
'уравне');
WriteLn ('ния (корни — любые числа)');
end;
WriteLn;
Write ('Для завершения программы нажмите');
WriteLn ('любую клавишу…');
repeat until KeyPressed; { Цикл ожидания нажатия любой клавиши }
end.
- 5.1. ОБЩИЕ СВЕДЕНИЯ О ПРОЕКТНОЙ ПРОЦЕДУРЕ
- 5.2. ИСТОРИЯ ВОЗНИКНОВЕНИЯ ПРОЕКТНОЙ ПРОЦЕДУРЫ
- 5.3. ОБЩЕЕ ОПИСАНИЕ ПРОЕКТНОЙ ПРОЦЕДУРЫ
- 5.4. РЕКОМЕНДАЦИИ НАЧИНАЮЩИМ ПО СОСТАВЛЕНИЮ ОПИСАНИЙ АЛГОРИТМОВ И ЭВРОРИТМОВ
- 5.5. ПРИМЕР РАЗРАБОТКИ ОПИСАНИЯ ПРОЦЕССА "КИПЯЧЕНИЕ ВОДЫ В ЧАЙНИКЕ"
- 5.6. ПРИМЕР ОПИСАНИЯ ПРОГРАММЫ "РЕДАКТОР ТЕКСТОВ"
- 5.7. РЕФАКТОРИНГ АЛГОРИТМОВ И ЭВРОРИТМОВ
- 5.8. КОДИРОВАНИЕ ТИПОВЫХ СТРУКТУР НА ЯЗЫКАХ ПРОГРАММИРОВАНИЯ
- 5.9. МЕТОДИКА РАЗРАБОТКИ АЛГОРИТМОВ ПРОГРАММ
- 5.10. ПРИМЕР ВЫПОЛНЕНИЯ УЧЕБНОЙ РАБОТЫ "РАЗРАБОТКА АЛГОРИТМА УМНОЖЕНИЯ"
- 5.11. ПРИМЕР ПРИМЕНЕНИЯ ПРОЕКТНОЙ ПРОЦЕДУРЫ ДЛЯ КОДИРОВАНИЯ ПРОГРАММЫ ПЕЧАТИ КАЛЕНДАРЯ НА ПРИНТЕРЕ
- Глава 5 ПРОЕКТНАЯ ПРОЦЕДУРА РАЗРАБОТКИ ФУНКЦИОНАЛЬНЫХ ОПИСАНИЙ
- 8.2. Языки программирования Виды программирований
- 1.1. Введение в объектно-ориентированное программирование
- 11.2. СВОЙСТВА ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- СТРУКТУРА ПРОСТОЙ ПРОГРАММЫ
- ПРИМЕР ПРОСТОЙ ПРОГРАММЫ НА ЯЗЫКЕ СИ
- 6.2. Типичные ошибки при проведении программ продвижения и варианты их устранения
- Системное программное обеспечение
- Язык программирования Python
- 1.2.5. Пример программы
- 24.7. Использование программы-твикера
- Программирование на языке Пролог для искусственного интеллекта




