Книга: Информационные операции в сети Интернет

Справочные функции

s = F_н(d,S) — функция определения (поиска) множества субъектов, у которых есть реальная возможность совершить множество действий d. Если речь идет об использовании государственных служащих в качестве субъектов при проведении информационной операции, то разработать данную функцию несложно. Функция Fsзадается на базе множества должностных обязанностей и инструкций. В ходе современной тенденции на стандартизацию сферы управления и перевода ее на стандарты ISO 9000 должностные обязанности становятся все более формализованными и создаются на базе стандартных шаблонов. Как правило, они не являются закрытыми и в рамках электронного правительства доступны через Интернет. А это значит, что при грамотном синтаксическом и семантическом анализе текстов инструкций по ведомствам и министерствам результат можно получать чуть ли не в режиме реального времени.

s = F_r(d,S) — функция определения (поиска) множество субъектов, потенциально готовых совершить множество действий d. Но при этом совсем не обязательно, что у них есть такая возможность. Получить значение для данной функции реально путем организации интернет-тестирования, интернет-панелей и т. п. способов тестирования и сбора данных о состоянии посетителей ресурсов.

m_d = F_m(s,d) — характеристика субъектов или материал, с которым согласны субъекты s, готовые совершить действия d.

d = F_d(m_d) — действия, которые готовы совершить субъекты, согласные с материалом m_d.

m_x = F_x(s) — тексты, характеризующие субъектов s. Как правило, эти данные получаются с помощью тестирования интернет-панелей.

t = F_t(d,S) — функция определения множества временных интервалов, в которые может быть совершено действие d. Частичная автоматизация данной функции возможна благодаря организации доступа к следующим данным:

* времени на распространение сообщений различных СМИ, включая ареал распространения. Например, для случая, когда действие — это доставка информации до определенной группы лиц. Все сказанное относится и к ресурсам сети Интернет. Только в случае сети — это число посетителей тех или иных сайтов с учетом географического расположения посетителей, что можно определять по IP-адресу посетителя;

* расписанию встреч должностных лиц на различных саммитах, встречах в верхах и т. п. Например, для случая, когда заявление, являющееся компонентом ИО, должно быть сделано по результатам именно встреч в верхах;

* расписанию конференций, праздников, знаменательных событий, дней рождения и т. п. Например, когда заявление, являющееся компонентом ИО, должно исходить от ученых или определенных известных лиц. В данном случае праздник — повод взятия интервью, приурочивание одного события к другому — информационному действию;

* расписанию работы должностных лиц, планам командировок и т. п. Например, ИО привязана к действиям должностных лиц. Так, к посещению высшими должностными лицами России Курильских островов, совершаемому по заранее известному плану, может быть специально подготовлена информационная акция, что и было сделано определенными кругами в Японии.

г = F_r(s) — функция определения множества ресурсов, которые посещаются субъектами s.

s = Fs(r) — множество субъектов, которые посещают ресурсы г.

z = Z_m(m_d) — стоимость создания материалов т.

z = Z_r(r) — стоимость охвата ресурсов г.

z = Z_-r(r) — стоимость блокирования ресурсов г.

Теперь перейдем к формализации самих действий.

?(m_d,k,r) — функция-действие, в ходе применения этой функции к раз осуществляется навязывание материала m_d на ресурсы г.

Для удобства восприятия будем считать, что область значения функции принадлежит множеству целых чисел от -N до +N, где (N = I S |.

N — материал для множества субъектов после размещения на ресурсе стал определяющим их поведение для всех субъектов.

0 — материал никак не повлиял на поведение субъектов.

-N — материал для множества субъектов изменил поведение всех на прямо противоположное.

При этом мы исходим из того, что распространяемые материалы подготовлены с учетом «правильного» восприятия зрителями и читателями. И не рассматриваем ситуацию, когда подготовленные материалы вызовут обратный эффект. Хотя подобный вариант довольно часто встречается на практике и вполне может быть использован для решения задач информационного противоборства.

Рассмотрим несколько вариантов планирования ИО, от простой операции до сложной.

ВАРИАНТ № 1. ПЛАНИРОВАНИЕ НА БАЗЕ ЕДИНОГО МАТЕРИАЛА

В этом случае формальная постановка задачи планирования ИО может быть сделана следующим образом:

Пусть d_ц — целевое действие, которое должны совершить субъекты S.

Для того чтобы оно было совершено, необходимо подготовить соответствующий этому действию материал и распространить его на множестве ресурсов, которые посещаются этими субъектами:

M_d = F_m(S,d_ц).

R = F_r(S).

Цель: максимизировать ?(?_d,?,R).

При следующих ограничениях:

1. Z_m(M_d) + n Z_r(R) + Z_-r(R) < Z₀ — финансовые средства, выделенные на подготовку и проведение ИО.

2. t(d_ц) ? T(d_ц) не пусто.

При такой постановке задачи планирование ИО сводится к подготовке материала M_d = F_m(S,d_ц), формированию и разведыванию множества ресурсов, посещаемых субъектами S.

Судя по публикуемым материалам СМИ, сегодня информационные операции именно так и готовятся. Нюансы не играют никакого значения — только массированное информационное давление. По схеме этого варианта раскручивается информационная операция применительно к Сирии, которую мы условно назвали «Химическое оружие. Сирия».

Предложим аналитическое выражение для функции ?(?_d,?,R). Очевидно, что значение этой функции тем больше, чем больше множество R, чем полнее соответствует материал M_d состоянию субъектов S (S = Fs(R)), и чем больше сделано попыток «навязать» данный материал — к.

С учетом сделанных предположений предлагается следующее аналитическое выражение:

?(?_d,?,R) = | S | (1 — (1 — | M_d ? F_x(S) | /| F_x(S)|)^k). (4.1)

Здесь

| S | — число посетителей ресурса R;

| M_d? F_x(S) | — похожесть[48] или выделение общего в текстах (материалах), которые характеризуют субъектов сейчас F_x(S), и M_d, которые должны характеризовать субъекты, способные совершить соответствующие действия. В данном случае предполагается, что операция пересечения множеств текстов M_d? F_x(S) оставит одинаковые в этих текстах формализованные поля. Результатом пересечения останется текст, состоящий из множества формализованных полей, присутствующих в обоих текстах в неизменном виде. Результатом оценки мощности полученного множества | M_d? F_x(S) | будет число общих полей (точек зрения).

| F_x(S)| — число формализованных полей в текстах, полученных в ходе тестирования субъектов S. Здесь надо помнить, что процесс тестирования может выполняться не обязательно в явной форме с согласия субъекта, но и в скрытой (путем задания непрямых вопросов), а также с привлечением экспертов (соседей, знакомых, коллег по работе, по соцсетям и т. п.).

(1 — (1 — | M_d? F_x(S) | /| F_x(S)|)^k) — оценка вероятности, что за к ознакомлений субъект S согласится с материалами M_d.

Если произвести замену S = Fs(R), чтобы исключить переменную S, которая отсутствует в явном виде в функции ?, то окончательный вариант будет таким:

?(?_d,?,R) = | FS(R) | (1 — (1 — | Md ? Fx(Fs(R)) | / | Fx(Fs(R))|)^к). (4.2)

ВАРИАНТ № 2. ПЛАНИРОВАНИЕ С УЧЕТОМ

ИНДИВИДУАЛЬНЫХ ОСОБЕННОСТЕЙ СУБЪЕКТОВ

В то же время учет индивидуальных предпочтений субъектов S способствовал бы повышению эффективности ИО и снижению общих затрат. Учет индивидуальных предпочтений возможен, если провести разбиение множества S на подмножества:

S = ? s_i,

и в дальнейшем готовить материал, ориентированный на конкретные подмножества субъектов. Тогда общая постановка задачи планирования будет выглядеть следующим образом.

Пусть d_ц — целевое действие, которое должны совершить субъекты S.

Для того чтобы оно было совершено, необходимо провести разбиение субъектов S по интересам и политическим предпочтениям, а затем подготовить соответствующий этому действию материал, ориентированный на конкретные группы субъектов:

m_di = F_m(Si,d_ц).

г_і = F_r(Si).

Max ??(m_di,к_і,г_і)

При следующих ограничениях:

1. ?Z_m(m_di) + ? n_i Z_r(r_i) + ??_-r(г_і) < Z_o — финансовые средства, выделенные на подготовку и проведение ИО.

2. t(d_ц) ? T(d_ц) не пусто.

При такой постановке задачи планирование ИО сводится к разбиению всего множества субъектов на подмножества по «интересам» и подготовке для каждого подмножества материалов, ориентированных именно на данное множество субъектов.

ВАРИАНТ № 3. ПЛАНИРОВАНИЕ С УЧЕТОМ

РАЗБИЕНИЯ ЦЕЛИ НА ПОДЦЕЛИ

При планировании ИО по первому и второму варианту мы исходили из того, что достижение цели осуществляется непосредственно на первом этапе ИО. Как правило, так оно и есть. Но в отдельных случаях, как, например, в случае информационной войны против СССР, достижение цели предполагало ряд этапов, т. е. чтобы достичь цели, надо было совершить целую последовательность дополняющих друг друга действий. Перепрограммирование осуществлялось этапно. Прежде чем перейти к подготовке субъектов на совершение d_ц действия, они готовились к совершению действий, близких к целевому.

В данном варианте планирование ИО осуществляется, начиная с построения цепочки множеств действий типа: d₁,d₂,d₃,…d_i,….d_ц. После чего по каждому множеству действий применяется вариант планирования № 2 или № 1.

В случае применения вариантов № 2 и № 1, а особенно № 1, адекватность распространяемой информации реальным процессам уже не играет никакой роли, важно только массированное информационное давление, важна только величина n_i в формуле ?(?_di,?_i,r_i), которая во многом определяется возможностями агрессора — Z_o.

Довольно часто для подтверждения своих текстов используются специально созданные фальшивки (m_i), особенно когда необходимо показать агрессивность и «бесчеловечность» той или иной страны и ее лидеров. Чтобы выйти на «дружное» осуждение исторического деятеля и факта, специально переписывается история. Реанимация из ничего якобы существовавшего действия dn, в конце-то концов, приводит к возможности реализации действия d_ц. Как гласит основной закон информационной войны: «Доказанная взаимосвязь несуществующих событий становится законом, определяющим поведение реальных субъектов»[49].

«Вот, скажем, такой пикантный моментик. По официальной версии Договор о ненападении между Германией и СССР и «секретный протокол» к этому договору были подписаны одновременно в Москве в рабочем кабинете Сталина в ночь с 23 на 24 августа 1939 г. Но почему-то они отпечатаны на разных пишущих машинках. Выходит, у Сталина была специальная пишущая машинка, на которой печатали только секретные сделки с Гитлером? Да, прямым доказательством подлога это не является, потому что гипотетически пишущая машинка после того, как на ней отпечатали текст договора, могла сломаться и «секретный протокол» к договору печатали на другой. Договор с «протоколом» отпечатаны на двух языках — русском и немецком. Для печати «секретного протокола» из советского комплекта использована тоже другая машинка с немецким шрифтом. Какова вероятность, что обе машинки — с русским шрифтом и немецким — сломаются одновременно?»[50] и т. д. еще десятки несоответствий.

Подробнее можно почитать в работе А. Кунгурова «Секретные протоколы, или Кто подделал пакт Молотова — Риббентропа»[51].

Это не единичный случай, подобных примеров по истории СССР достаточно много. Они были нужны, чтобы создать образ жуткого врага, для уничтожения которого годятся любые средства.

Демонизировать Сталина необходимо не ради демонизации, а ради настоящего и будущего. Происшедшие события забываются, свидетели умирают, архивы переписываются. В этих условиях история, как и любая религия, формируется опираясь на веру. Например, есть событие — атомная бомбардировка японских городов. Кто палач, отдавший приказ? Злодеи коммунисты или свободолюбивые демократы? Ответ понятен и не требует доказательств. Ибо только злодеи на подобное способны.

В информационную эпоху создавать фальшивки стало проще, используя соответствующее программное обеспечение, а распространять еще проще, благодаря Интернету, куда сегодня и переместился основной центр изготовления и распространения фальшивок.

Как уже говорилось выше, через d мы обозначаем множество однотипных действий, которые могут выполняться параллельно. В условиях информационной войны против СССР последовательность была немаленькой, перечисление хватило было для хорошего отчета не на одну тысячу страниц. Для удобства иллюстрации мы выбрали более простой пример ИО, включающий в себя последовательность всего из трех множеств действий: d₁, d₂, d₃, d_ц.

Схема информационной операции по дискредитации интернетресурса приведена на рис. 4.1.2.1.

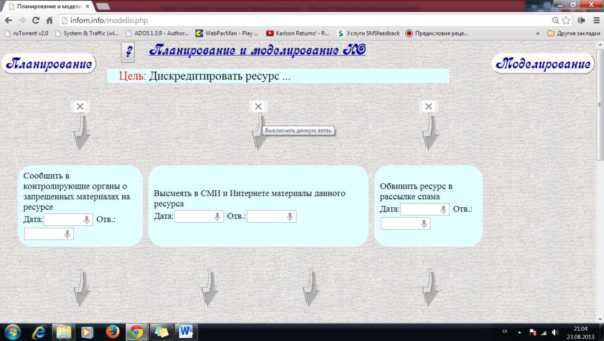
РИСУНОК 4.1.2.1 Схема по дискредитации интернет-ресурса

На рис. 4.1.2.2. изображено следующее дерево действий:

Целевое действие (d_ц):

— дискредитировать ресурс.

Действия, приводящие к целевому (d₃):

— сообщить в контролирующие органы о запрещенных материалах на ресурсе;

— высмеять в СМИ и Интернете материалы данного ресурса;

— обвинить ресурс в рассылке спама.

Действия, приводящие к d₃ (d₂):

— разместить на ресурсе материалы, подпадающие под запрещенные (методы размещения: взлом ресурса, комментарии к новостям, форум/чат);

— разместить на ресурсе материалы издевательского над ресурсом характера (методы размещения: взлом ресурса, комментарии к новостям, форум/чат);

— создать искаженное зеркало ресурса (методы: создание и регистрация специального собственного сайта);

— организовать почтовую рассылку спама от имени данного ресурса (методы: организовать анонимный доступ в Интернет).

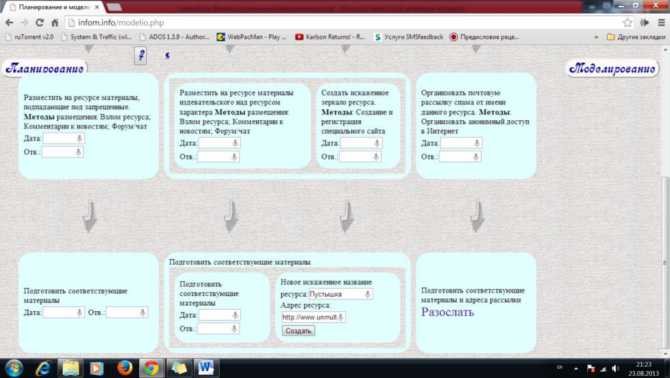
РИСУНОК 4.1.2.2. Пример дерева действий

Действия, приводящие к d₂ (d₁):

— подготовить соответствующие материалы;

— придумать новое искаженное (издевательское) название ресурса;

— подготовить соответствующий спам и адреса рассылки.

Затем подготовленная схема наполняется адресами конкретных ресурсов (R). Далее осуществляется предварительный анализ, на основании которого проводится оценка стоимости и времени на выполнение действий плана. После чего выполняется окончательный расчет и общая оценка вероятности достижения цели.

Оглавление книги