Книга: Real-Time Concepts for Embedded Systems
16.3.2 Deadlock Detection
Разделы на этой странице:
16.3.2 Deadlock Detection
A deadlock condition is called a stable deadlock when no task in the deadlocked set expects a timeout or an abort that can eliminate the deadlock. A stable deadlock is permanent and requires external influence to eliminate. The external influence is the deadlock detection and recovery by the underlying RTOS.
Deadlock detection is the periodic deployment of an algorithm by the RTOS. The algorithm examines the current resource allocation state and pending resource requests to determine whether deadlock exists in the system, and if so, which tasks and resources are involved.
The deadlock detection algorithm that the RTOS deploys is a global algorithm because it is used to detect deadlocks in the entire system. In general, each task of the deadlocked set is not aware of the deadlock condition. As a result, the recovery algorithm is more intrusive on the normal execution of the tasks belonging to the deadlocked set. The recovery algorithms and reasons why these algorithms are intrusive on the execution of the tasks involved in the deadlock are discussed shortly.
A temporal deadlock is a temporary deadlock situation in which one or more tasks of the deadlocked set either times out or aborts abnormally due to timing constraints. When the task times out or aborts, it frees the resources that might have caused the deadlock in the first place, thus eliminating the deadlock. This form of detection and recovery is localized to an individual task, and the task has deadlock awareness.
A system that is capable of deadlock detection is more efficient in terms of resource utilization when compared to a system without deadlock detection. A system capable of deadlock detection is not conservative when granting resource allocation requests if deadlock is allowed to occur. Therefore, resources are highly utilized. A system without deadlock detection is conservative when granting resource allocation requests. A resource request is denied if the system believes there is a potential for deadlock, which may never occur. The conservatism of the system results in idle resources even when these resources could be used.
Deadlock detection does not solve the problem; instead, the detection algorithm informs the recovery algorithm when the existence of deadlock is discovered.
For deadlock in the Single resource request model, a cycle in the resource graph is a necessary and sufficient condition.
For deadlock in the AND resource request model, a cycle in the resource graph is a necessary and sufficient condition. It is possible for a task to be involved in multiple deadlocked sets.
For deadlock in the OR request model, a knot is a necessary and sufficient condition.
Therefore, deadlock detection involves finding the presence of a cycle in the resource graph for both the Single and the AND resource request models. Deadlock detection involves finding the presence of a knot in the resource graph for the OR resource request model.
For deadlock in the AND-OR model, no simple way exists of describing it. Generally, the presence of a knot after applying the algorithm to the OR model first and then subsequently applying the algorithm to the AND model and finding a cycle is an indication that deadlock is present.
The following sections present two deadlock detection algorithms-one for the single resource request model and one for the AND resource request model-to illustrate deadlock detection in practice.
For node A in the resource graph, the reachable set of A is the set of all nodes B, such that a directed path exists from A to B. A knot is the request set K, such that the reachable set of each node of K is exactly K.
Single-Instance Resource Deadlock Detection
The deadlock detection algorithm for systems with a single instance of each resource type, and tasks making resource requests following the single resource request model, is based on the graph theory. The idea is to find cycles in the resource allocation graph, which represents the circular-wait condition, indicating the existence of deadlocks.
Figure 16.3 shows the resource allocation graph. The graph represents the following:
· a circle represents a resource,
· a square represents a task or thread of execution,
· an arrow going from a task to a resource indicates that the task wants the resource, and
· an arrow going from a resource to a task indicates that the task currently holds the resource.
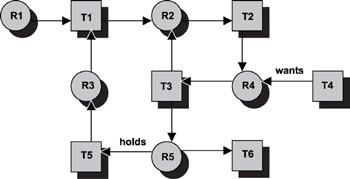
Figure 16.3: Current state of resource allocations and requests.
In the following discussions, node refers either to the circle (resource) or the square (task) in Figure 16.3. Arc refers to the arrow. The deadlock detection algorithm can be stated in these seven steps:
1. Make a list of all the nodes, N, from the graph.
2. Pick a node from N. Create another list, L, initially empty, which is used for the graph traversal.
3. Insert the node into L and check if this node already exists in L. If so, a cycle exists; therefore, a deadlock is detected, and the algorithm terminates. Otherwise, remove the node from N.
4. Check whether any un-traversed outgoing arcs from this node exist. If all of the arcs are traversed, go to step 6.
5. Choose an un-traversed outgoing arc originating from the node and mark the arc as traversed. Follow the chosen arc to the new node and return to step 3.
6. At this stage, a path in the graph terminates, and no deadlocks exist. If more than one entry is in L, remove the last entry from L. If more than one entry remains in L, make the last entry of L the current node and go to step 4.
7. If the list N is not empty, go to step 2. Otherwise, the algorithm terminates, and no deadlocks exist in the system.
The actual implementation from step 3 to step 6 translates into a depth first search of the directed graph.
Applying this algorithm to the system depicted in Figure 16.3 provides the following:
Step 1: N = {R1, T1, R2, T2, R3, T3, R4, T4, T5, R5, T6}
Step 2: L = {‹empty›}; pick node R1
Step 3: L = {R1}; no cycles are in L; N = {T1, R2, T2, R3, T3, R4, T4, T5, R5, T6}
Step 4: R1 has one outgoing arc
Step 5: Mark the arc; reaches node T1; go back to step 3
Step 3: L = {R1, T1}; N = {R2, T2, R3, T3, R4, T4, T5, R5, T6}; no cycles are in L
The algorithm continues from step 3 to step 5 and reiterates until it reaches node T3, in which the list L = {R1, T1, R2, T2, R4, T3} and the list N = {R3, T4, T5, R5, T6}. Two outgoing arcs are at node T3. When the downward arc is picked, L = {R1, T1, R2, T2, R4, T3, R5}. Two outgoing arcs are at node R5. When the rightward arc is picked, L = {R1, T1, R2, T2, R4, T3, R5, T6}.
Step 4: T6 does not have any outgoing arcs; continue to step 6
Step 6: Remove T6 from the list L; L = {R1, T1, R2, T2, R4, T3, R5}; return to step 4
Step 4: Pick the unmarked leftward arc at R5
Step 5: Mark the arc; reaches node T5; return to step 3
Step 3: L = {R1, T1, R2, T2, R4, T3, R5, T5}; N = {R3, T4}; no cycles are in L
Step 4: Pick the only outgoing arc at T5
Step 5: Mark the arc; reaches node R3; go back to step 3
Step 3: L = {R1, T1, R2, T2, R4, T3, R5, T5, R3}; N = {T4}; still no cycles are in L
Step 4: Pick the only outgoing arc at R3
Step 5: Mark the arc; reaches node T1; go back to step 3
Step 3: L = {R1, T1, R2, T2, R4, T3, R5, T5, R3, T1}; Node T1 already exists in L. A cycle is found in the graph, and a deadlock exists. The algorithm terminates.
The deadlock set is comprised of the entire nodes enclosed by the two occurrences of node T1 inclusively. Therefore, the discovered deadlock set is {T1, R2, T2, R4, T3, R5, T5, R3}. One thing worth noting is that the algorithm detects deadlocks if any exist. Which deadlock is detected first depends on the structure of the graph. Closer examination of the resource graph reveals that another deadlock exists. That deadlock set is {R2, T2, R4, T3}. At node T3 if the upward arc is chosen first instead of the downward arc, this later deadlock occurrence would be discovered, and the algorithm would terminate much sooner.
Multi-Instance Resource Deadlock Detection
The deadlock detection algorithm takes a different approach for systems with multiple instances of each resource type, and tasks make resource requests following the AND model. An underlying assumption is that a resource allocation system is present. The resource allocation system is comprised of a set of different types of resources, R1, R2, R3,…, Rn. Each type of resource has a fixed number of units. The resource allocation system maintains a resource allocation table and a resource demand table.
Each row of tables C and D represents a task T. Each column of tables C and D is associated with a resource type. C is the resource allocation table representing resources already allocated. D is the resource demand table representing additional resources required by the tasks.
| N = Total System Resources Table | N1 | N2 | N3 | … | Nk |
where Ni is the number of units of resource type Ri for all i where {1 ? i ? k }.
| A = Available System Resources Table | A1 | A2 | A3 | … | Ak |
where Ai the number of units remaining for resource type Ri available for allocation.
| C = Tasks Resources Assigned Table | C11 | C12 | C13 | … | C1k |
| C21 | C22 | … | C2k | ||
| … | … | ||||
| Cm1 | … | Cmk | |||
| D = Tasks Resources Demand Table | D11 | D12 | D13 | … | D1k |
| D21 | D22 | … | D2k | ||
| … | … | ||||
| Dm1 | … | Dmk |
For example in table C, there are C11 units of resource R1, C12 units of resource R2, and so on, which are allocated to task T1. Similarly, there are C21 units of resource R1, C22 units of resource R2, and so on, which are allocated to task T2. For example in table D, task T1 demands additional D11 units of resource R1, additional D12 units of resource R2, and so on, in order to complete execution.
The deadlock detection algorithm is as follows:
1. Find a row i in table D, where Dij ‹ Aj for all 1 ? j ? k. If no such row exists, the system is deadlocked, and the algorithm terminates.
2. Mark the row i as complete and assign Aj = Aj + Dij for all 1 ? j ? k.
3. If an incomplete row is present, return to step 1. Otherwise, no deadlock is in the system, and the algorithm terminates.
Step 1 of the algorithm looks for a task whose resource requirements can be satisfied. If such a task exists, the task can run to completion. Resources from the completed task are freed back into the resource pool, which step 2 does. The newly available resources can be used to meet the requirements of other tasks, which allow them to resume execution and run to completion.
When the algorithm terminates, the system is deadlocked if table T has incomplete rows. The incomplete rows represent the tasks belonging to the deadlocked set. The algorithm is illustrated in the following example.
| N = | 4 | 6 | 2 | |
| A = | 1 | 2 | 0 | |
| C = | 0 | 2 | 0 | Task 1 |
| 1 | 1 | 0 | Task 2 | |
| 1 | 1 | 1 | Task 3 | |
| 1 | 0 | 1 | Task 4 | |
| D = | 2 | 2 | 2 | Task 1 |
| 1 | 1 | 0 | Task 2 | |
| 0 | 1 | 0 | Task 3 | |
| 1 | 1 | 1 | Task 4 |
Step 1: Task 1 cannot continue because the available resources do not satisfy its requirements.
Task 2 can continue because what it needs can be met.
| Step 2: | A = 2 | 3 | 0 |
Step 3: Task 1, task 3, and task 4 remain. Return to step 1.
Step 1: Task 1 still cannot continue. The requirement from task 3 can be met.
| Step 2: | A = 3 | 4 | 1 |
Step 3: Task 1 and task 4 remain. Return to step 1.
Step 1: Task 1 still cannot continue, but task 4 can.
| Step 2: | A = 4 | 4 | 2 |
Step 3: Task 1 remains. Return to step 1.
Step 1: Task 1 can continue.
| Step 2: | A = 4 | 6 | 2 |
Step 3: No more tasks remain, and the algorithm terminates. No deadlock is in the system.
Now if the resource requirement for task 3 were [0 1 1] instead of [0 1 0], task 1, task 3, and task 4 cannot resume execution due to lack of resources. In this case, these three tasks are deadlocked.
It is worth noting that executing a deadlock detection algorithm takes time and can be non-deterministic.




