Книга: Distributed operating systems

3.5.1. Distributed Deadlock Detection

3.5.1. Distributed Deadlock Detection

Finding general methods for preventing or avoiding distributed deadlocks appears to be quite difficult, so many researchers have tried to deal with the simpler problem of just detecting deadlocks, rather than trying to inhibit their occurrence.

However, the presence of atomic transactions in some distributed systems makes a major conceptual difference. When a deadlock is detected in a conventional operating system, the way to resolve it is to kill off one or more processes. Doing so invariably leads to one or more unhappy users. When a deadlock is detected in a system based on atomic transactions, it is resolved by aborting one or more transactions. But as we have seen in detail above, transactions have been designed to withstand being aborted. When a transaction is aborted because it contributes to a deadlock, the system is first restored to the state it had before the transaction began, at which point the transaction can start again. With a little bit of luck, it will succeed the second time. Thus the difference is that the consequences of killing off a process are much less severe when transactions are used than when they are not used.

As a first attempt, we can use a centralized deadlock detection algorithm and try to imitate the nondistributed algorithm. Although each machine maintains the resource graph for its own processes and resources, a central coordinator maintains the resource graph for the entire system (the union of all the individual graphs). When the coordinator detects a cycle, it kills off one process to break the deadlock.

Unlike the centralized case, where all the information is automatically available in the right place, in a distributed system it has to be sent there explicitly. Each machine maintains the graph for its own processes and resources. Several possibilities exist for getting it there. First, whenever an arc is added or deleted from the resource graph, a message can be sent to the coordinator providing the update. Second, periodically, every process can send a list of arcs added or deleted since the previous update. This method requires fewer messages than the first one. Third, the coordinator can ask for information when it needs it.

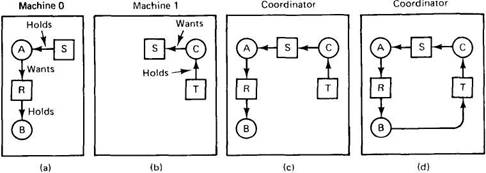
Fig. 3-23. (a) Initial resource graph for machine 0. (b) Initial resource graph for machine 1. (c) The coordinator's view of the world. (d) The situation after the delayed message.

Unfortunately, none of these methods work well. Consider a system with processes A and B running on machine 0, and process C running on machine 1. Three resources exist: R, S, and T. Initially, the situation is as shown in Fig. 3-23(a) and (b): A holds S but wants R, which it cannot have because B is using it; C has T and wants S, too. The coordinator's view of the world is shown in Fig. 3-23(c). This configuration is safe. As soon as B finishes, A can get R and finish, releasing S for C.

After a while, B releases R and asks for T, a perfectly legal and safe swap. Machine 0 sends a message to the coordinator announcing the release of R, and machine 1 sends a message to the coordinator announcing the fact that B is now waiting for its resource, T. Unfortunately, the message from machine 1 arrives first, leading the coordinator to construct the graph of Fig. 3-23(d). The coordinator incorrectly concludes that a deadlock exists and kills some process. Such a situation is called a false deadlock. Many deadlock algorithms in distributed systems produce false deadlocks like this due to incomplete or delayed information.

One possible way out might be to use Lamport's algorithm to provide global time. Since the message from machine 1 to the coordinator is triggered by the request from machine 0, the message from machine 1 to the coordinator will indeed have a later timestamp than the message from machine 0 to the coordinator. When the coordinator gets the message from machine 1 that leads it to suspect deadlock, it could send a message to every machine in the system saying: "I just received a message with timestamp T which leads to deadlock. If anyone has a message for me with an earlier timestamp, please send it immediately." When every machine has replied, positively or negatively, the coordinator will see that the arc from R to B has vanished, so the system is still safe. Although this method eliminates the false deadlock, it requires global time and is expensive. Furthermore, other situations exist where eliminating false deadlock is much harder.

Many distributed deadlock detection algorithms have been published. Surveys of the subject are given in Knapp (1987) and Singhal (1989). Let us examine a typical one here, the Chandy-Misra-Haas algorithm (Chandy et al., 1983). In this algorithm, processes are allowed to request multiple resources (e.g., locks) at once, instead of one at a time. By allowing multiple requests simultaneously, the growing phase of a transaction can be speeded up considerably. The consequence of this change to the model is that a process may now wait on two or more resources simultaneously.

In Fig. 3-24, we present a modified resource graph, where only the processes are shown. Each arc passes through a resource, as usual, but for simplicity the resources have been omitted from the figure. Notice that process 3 on machine 1 is waiting for two resources, one held by process 4 and one held by process 5.

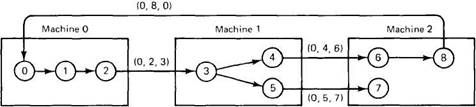
Fig. 3-24. The Chandy-Misra-Haas distributed deadlock detection algorithm.

Some of the processes are waiting for local resources, such as process 1, but others, such are process 2, are waiting for resources that are located on a different machine. It is precisely these cross-machine arcs that make looking for cycles difficult. The Chandy-Misra-Haas algorithm is invoked when a process has to wait for some resource, for example, process 0 blocking on process 1. At that point a special probe message is generated and sent to the process (or processes) holding the needed resources. The message consists of three numbers: the process that just blocked, the process sending the message, and the process to whom it is being sent. The initial message from 0 to 1 contains the triple (0, 0, 1).

When the message arrives, the recipient checks to see if it itself is waiting for any processes. If so, the message is updated, keeping the first field but replacing the second field by its own process number and the third one by the number of the process it is waiting for. The message is then sent to the process on which it is blocked. If it is blocked on multiple processes, all of them are sent (different) messages. This algorithm is followed whether the resource is local or remote. In Fig. 3-24 we see the remote messages labeled (0, 2, 3), (0, 4, 6), (0, 5, 7), and (0, 8, 0). If a message goes all the way around and comes back to the original sender, that is, the process listed in the first field, a cycle exists and the system is deadlocked.

There are various ways in which the deadlock can be broken. One way is to have the process that initiated the probe commit suicide. However, this method has problems if several processes invoke the algorithm simultaneously. In Fig. 3-24, for example, imagine that both 0 and 6 block at the same moment, and both initiate probes. Each would eventually discover the deadlock, and each would kill itself. This is overkill. Getting rid of one of them is enough.

An alternative algorithm is to have each process add its identity to the end of the probe message so that when it returned to the initial sender, the complete cycle would be listed. The sender can then see which process has the highest number, and kill that one or send it a message asking it to kill itself. Either way, if multiple processes discover the same cycle at the same time, they will all choose the same victim.

There are few areas of computer science in which theory and practice diverge as much as in distributed deadlock detection algorithms. Discovering yet another deadlock detection algorithm is the goal of many a researcher. Unfortunately, these models often have little relation to reality. For example, some of the algorithms require processes to send probes when they are blocked. However, sending a probe when you are blocked is not entirely trivial.

Many of the papers contain elaborate analyses of the performance of the new algorithm, pointing out, for example, that while the new one requires two traversals of the cycle, it uses shorter messages, as if these factors balanced out somehow. The authors would no doubt be surprised to learn that a typical "short" message (20 bytes) on a LAN takes about 1 msec, and a typical "long" message (100 bytes) on the same LAN takes perhaps 1.1 msec. It would also no doubt come as a shock to these people to realize that experimental measurements have shown that 90 percent of all deadlock cycles involve exactly two processes (Gray et al., 1981).

Worst of all, a large fraction of all the published algorithms in this area are just plain wrong, including those proven to be correct. Knapp (1987) and Singhal (1989) point out some examples. It often occurs that shortly after an algorithm is invented, proven correct, and then published, somebody finds a counterexample. Thus we have an active research area in which the model of the problem does not correspond well to reality, the solutions found are generally impractical, the performance analyses given are meaningless, and the proven results are frequently incorrect. To end on a positive note, this is an area that offers great opportunities for improvement.

Оглавление книги