Книга: Real-Time Concepts for Embedded Systems

13.2.3 Finding Free Blocks Quickly

13.2.3 Finding Free Blocks Quickly

In this memory management scheme, malloc always allocates from the largest available range of free blocks. The allocation array described is not arranged to help malloc perform this task quickly. The entries representing free ranges are not sorted by size. Finding the largest range always entails an end-to-end search. For this reason, a second data structure is used to speed up the search for the free block that can satisfy the allocation request. The sizes of free blocks within the allocation array are maintained using the heap data structure, as shown in Figure 13.4. The heap data structure is a complete binary tree with one property: the value contained at a node is no smaller than the value in any of its child nodes.

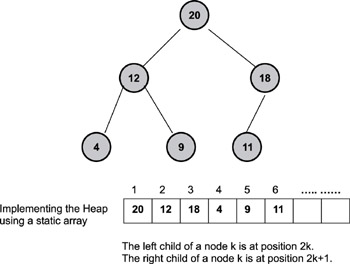
Figure 13.4: Free blocks in a heap arrangement.

The size of each free block is the key used for arranging the heap. Therefore, the largest free block is always at the top of the heap. The malloc algorithm carves the allocation out of the largest available free block. The remaining portion is reinserted into the heap. The heap is rearranged as the last step of the memory allocation process.

Although the size of each free range is the key that organizes the heap, each node in the heap is actually a data structure containing at least two pieces of information: the size of a free range and its starting index in the allocation array. The malloc operation involves the following steps:

1. Examine the heap to determine if a free block that is large enough for the allocation request exists.

2. If no such block exists, return an error to the caller.

3. Retrieve the starting allocation-array index of the free range from the top of the heap.

4. Update the allocation array by marking the newly allocated block, as illustrated in Figure 13.3.

5. If the entire block is used to satisfy the allocation, update the heap by deleting the largest node. Otherwise update the size.

6. Rearrange the heap array.

Before any memory has been allocated, the heap has just one node, signifying that the entire memory region is available as one, large, free block. The heap continues to have a single node either if memory is allocated consecutively without any free operations or if each memory free operation results in the deallocated block merging with its immediate neighbors. The heap structure in Figure 13.4 represents free blocks interleaved with blocks in use and is similar to the memory map in Figure 13.2.

The heap can be implemented using another static array, called the heap array, as shown in Figure 13.4. The array index begins at 1 instead of 0 to simplify coding in C. In this example, six free blocks of 20, 18, 12, 11, 9, and 4 blocks are available. The next memory allocation uses the 20-block range regardless of the size of the allocation request. Note that the heap array is a compact way to implement a binary tree. The heap array stores no pointers to child nodes; instead, child-parent relationships are indicated by the positions of the nodes within the array.

Оглавление книги