Книга: Программист-прагматик. Путь от подмастерья к мастеру

Система обозначений О()

Система обозначений О()

Система O() представляет собой математический способ обозначения приближений. Если мы указываем, что некая программа осуществляет сортировку n записей за время O(n^2), то это просто означает, что максимальное время выполнения программы будет изменяться пропорционально n^2. При удвоении числа записей время возрастет примерно в четыре раза. O() можно рассматривать как порядок величины. Система обозначений O() определяет верхнюю границу величины измеряемого параметра (время, объем памяти, и т. д.). Если мы говорим, что некая функция занимает время O(n^2), то под этим понимается, что верхняя граница интервала времени, необходимого для ее выполнения, возрастает не быстрее n^2. Иногда мы встречаемся с довольно сложными функциями O(), и поскольку именно член высшего порядка будет определять значение с ростом n, то обычно все члены низшего порядка удаляются, чтобы не мешать постоянным коэффициентам умножения. O(n^2/2+Зn) означает то же самое, что и O(n^2/2), которое, в свою очередь, является эквивалентом O(n^2). В этом и состоит недостаток системы обозначений O() – один алгоритм O(n^2) может быть быстрее другого алгоритма O(n^2) в тысячу раз, но из обозначений вы этого не поймете.

На рисунке 6.1 показано несколько общих обозначений O(), с которым вы можете встретиться, и график, на котором сравнивается время выполнения алгоритмов в каждой категории. Из него ясно, что все начинает быстро выходить из-под контроля, как только мы переходим через O(n^2).

Рис. 6.1. Время выполнения различных алгоритмов

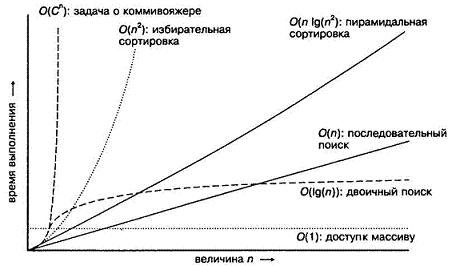
Некоторые универсальные обозначения О-большое

O(1) Постоянная зависимость (обращение к элементу массива, простые операторы)

O(lg(n)) Логарифмическая зависимость (двоичный поиск) [lg(n) – краткое обозначение log2(n)]

O(n) Линейная зависимость (последовательный поиск)

O(n lg(n)) Эта зависимость линейной, но не намного (среднее время быстрой сортировки, пирамидальной сортировки)

O(n^2) Квадратичная зависимость (выборочная сортировка и сортировка включения)

O(n^3) Кубическая зависимость (перемножение двух матриц размером n*n)

O(C^n) Экспоненциальная зависимость (задача о коммивояжере, разбиение набора)

Предположим, что у вас есть программа, обрабатывающая 100 записей за 1 сек. Сколько времени ей потребуется для обработки 1000 записей? Если ваша программа является O(1), то это время остается равным 1 сек. Если она является O(lg(n)), то для обработки потребуется около 3 сек. При O(n) время обработки линейно возрастает до 10 сек., а при O(nlg(n)) составит примерно 33 сек. Если вам не повезло и ваша программа является O(n^2), то можете отдохнуть в течение 100 сек., пока она не сделает свое дело. Ну а в том случае, если вы используете экспоненциальный алгоритм O(2^n), можете заварить чашечку кофе – программа завершит свою работу примерно через 10263 года. В общем, хотелось бы знать, как происходит конец света.

Система обозначений O() не применяется только к временным параметрам; ее можно использовать для представления других ресурсов, требуемых неким алгоритмом. Например, она часто является полезной при моделировании расхода памяти (см. упражнение 35).

Оглавление книги