Книга: Технология XSLT

Деревья

Деревья

Прежде, чем мы приступим к рассмотрению типов узлов и отношений между ними, необходимо определиться с самой структурой дерева. Древовидная структура задает для своих элементов отношение ветвления, очень похожее на строение обычного дерева — есть корневой узел (ствол), от которого происходят другие узлы (ветки).

Формально [Кнут 2000] дерево определяется, как конечное множество T, состоящее из одного или нескольких элементов (узлов), обладающих следующими свойствами:

? во множестве T выделяется единственный узел, называемый корневым узлом или корнем;

? все остальные узлы разделены на m?0 непересекающихся множеств T₁, …, T_m, каждое из которых в свою очередь также является деревом.

Деревья T₁, …, T_m называются поддеревьями корня дерева T.

Это определение является рекурсивным, то есть в нем дерево определяется само через себя. Конечно, существуют нерекурсивные определения, но, пожалуй, следует согласиться с тем, что рекурсивное определение лучше всего отражает суть древовидной структуры: ветки дерева также являются деревьями.

В XSLT и XPath деревья являются упорядоченными, то есть для множеств T₁, …, T_m задается порядок следования, который называется порядком просмотра документа. В XSLT деревья упорядочиваются в порядке появления текстового представления их узлов в документах.

Существует множество способов графического изображения деревьев. Мы будем рисовать их так, что корень дерева будет находиться наверху, а поддеревья будут упорядочены слева направо. Такой способ является довольно стандартным для XML, хотя и здесь существует множество вариантов. Примером изображения дерева может быть следующий рисунок (рис. 3.2):

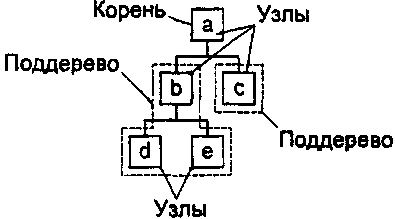
Рис. 3.2. Изображение дерева

Мы часто будем говорить о дочерних узлах, родительских узлах, братских узлах, узлах-предках и узлах-потомках. Дадим определения этим понятиям.

? Дочерним узлом текущего узла называется любой из корней его поддеревьев. Например, в дереве на рис. 3.2 дочерними узлами узла а являются узлы b и с, а дочерними узлами узла b — узлы d и e. Узел с не имеет дочерних узлов — такие узлы иначе называются листьями.

? Каждый узел называется родительским узлом корней своих поддеревьев. На рис. 3.2 узел а является родителем узлов b и с, а узел b — родителем узлов d и e.

? Корни поддеревьев называются братскими узлами или узлами-братьями. На рис. 3.2 братьями являются узлы b и с, а также узлы d и e.

? Предками текущего узла являются его родитель, а также родители его родителей и так далее. На рис. 3.2 предками узла d являются узлы b и а.

? Потомками текущего узла являются его дочерние узлы, а также дочерние узлы его дочерних узлов и так далее. На рис. 3.2 потомками узла а являются узлы b, c, d и e.

Оглавление книги