Книга: Distributed operating systems

2.5.2. Design Issues

2.5.2. Design Issues

Group communication has many of the same design possibilities as regular message passing, such as buffered versus unbuffered, blocking versus nonblock-ing, and so forth. However, there are also a large number of additional choices that must be made because sending to a group is inherently different from sending to a single process. Furthermore, groups can be organized in various ways internally. They can also be addressed in novel ways not relevant in point-to-point communication. In this section we will look at some of the most important design issues and point out the various alternatives.

Systems that support group communication can be divided into two categories depending on who can send to whom. Some systems support closedgroups, in which only the members of the group can send to the group. Outsiders cannot send messages to the group as a whole, although they may be able to send messages to individual members. In contrast, other systems support opengroups, which do not have this property. When open groups are used, any process in the system can send to any group. The difference between closed and open groups is shown in Fig. 2-31.

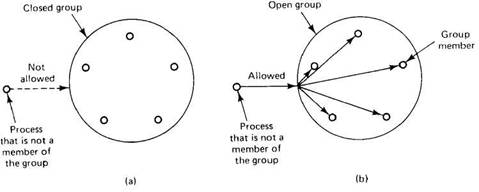
Fig. 2-31. (a) Outsiders may not send to a closed group. (b) Outsiders may send to an open group.

The decision as to whether a system supports closed or open groups usually relates to the reason groups are being supported in the first place. Closed groups are typically used for parallel processing. For example, a collection of processes working together to play a game of chess might form a closed group. They have their own goal and do not interact with the outside world.

On the other hand, when the idea of groups is to support replicated servers, it is important that processes that are not members (clients) can send to the group. In addition, the members of the group may also need to use group communication, for example to decide who should carry out a particular request. The distinction between closed and open groups is often made for implementation reasons.

The distinction between closed and open groups relates to who can communicate with the group. Another important distinction has to do with the internal structure of the group. In some groups, all the processes are equal. No one is boss and all decisions are made collectively. In other groups, some kind of hierarchy exists. For example, one process is the coordinator and all the others are workers. In this model, when a request for work is generated, either by an external client or by one of the workers, it is sent to the coordinator. The coordinator then decides which worker is best suited to carry it out, and forwards it there. More complex hierarchies are also possible, of course. These communication patterns are illustrated in Fig. 2-32.

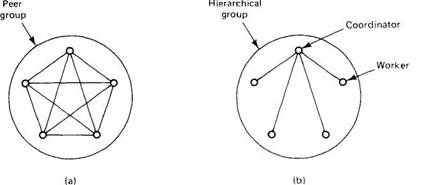
Fig. 2-32. (a) Communication in a peer group. (b) Communication in a simple hierarchical group.

Each of these organizations has its own advantages and disadvantages. The peer group is symmetric and has no single point of failure. If one of the processes crashes, the group simply becomes smaller, but can otherwise continue. A disadvantage is that decision making is more complicated. To decide anything, a vote has to be taken, incurring some delay and overhead.

The hierarchical group has the opposite properties. Loss of the coordinator brings the entire group to a grinding halt, but as long as it is running, it can make decisions without bothering everyone else. For example, a hierarchical group might be appropriate for a parallel chess program. The coordinator takes the current board, generates all the legal moves from it, and farms them out to the workers for evaluation. During this evaluation, new boards are generated and sent back to the coordinator to have them evaluated. When a worker is idle, it asks the coordinator for a new board to work on. In this manner, the coordinator controls the search strategy and prunes the game tree (e.g., using the alpha-beta search method), but leaves the actual evaluation to the workers.

When group communication is present, some method is needed for creating and deleting groups, as well as for allowing processes to join and leave groups. One possible approach is to have a group server to which all these requests can be sent. The group server can then maintain a complete data base of all the groups and their exact membership. This method is straightforward, efficient, and easy to implement. Unfortunately, it shares with all centralized techniques a major disadvantage: a single point of failure. If the group server crashes, group management ceases to exist. Probably most or all groups will have to be reconstructed from scratch, possibly terminating whatever work was going on.

The opposite approach is to manage group membership in a distributed way. In an open group, an outsider can send a message to all group members announcing its presence. In a closed group, something similar is needed (in effect, even closed groups have to be open with respect to joining). To leave a group, a member just sends a goodbye message to everyone.

So far, all of this is straightforward. However, there are two issues associated with group membership that are a bit trickier. First, if a member crashes, it effectively leaves the group. The trouble is, there is no polite announcement of this fact as there is when a process leaves voluntarily. The other members have to discover this experimentally by noticing that the crashed member no longer responds to anything. Once it is certain that the crashed member is really down, it can be removed from the group.

The other knotty issue is that leaving and joining have to be synchronous with messages being sent. In other words, starting at the instant that a process has joined a group, it must receive all messages sent to that group. Similarly, as soon as a process has left a group, it must not receive any more messages from the group, and the other members must not receive any more messages from it. One way of making sure that a join or leave is integrated into the message stream at the right place is to convert this operation into a message sent to the whole group.

One final issue relating to group membership is what to do if so many machines go down that the group can no longer function at all. Some protocol is needed to rebuild the group. Invariably, some process will have to take the initiative to start the ball rolling, but what happens if two or three try at the same time? The protocol will have to be able to withstand this.

Inorder to send a message to a group, a process must have some way of specifying which group it means. In other words, groups need to be addressed, just as processes do. One way is to give each group a unique address, much like a process address. If the network supports multicast, the group address can be associated with a multicast address, so that every message sent to the group address can be multicast. In this way, the message will be sent to all those machines that need it, and no others.

If the hardware supports broadcast but not multicast, the message can be broadcast. Every kernel will then get it and extract from it the group address. If none of the processes on the machine is a member of the group, the broadcast is simply discarded. Otherwise, it is passed to all group members.

Finally, if neither multicast nor broadcast is supported, the kernel on the sending machine will have to have a list of machines that have processes belonging to the group. The kernel then sends each one a point-to-point message. These three implementation methods are shown in Fig. 2-33. The thing to notice is that in all three cases, a process just sends a message to a group address and it is delivered to all the members. How that happens is up to the operating system. The sender is not aware of the size of the group or whether communication is implemented by multicasting, broadcasting, or unicasting.

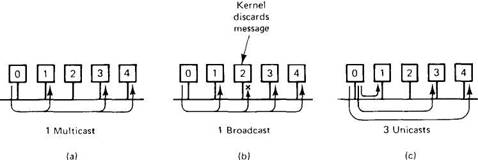
Fig. 2-33. Process 0 sending to a group consisting of processes 1,3, and 4. (a) Multicast implementation. (b) Broadcast implementation. (c) Unicast implementation.

A second method of group addressing is to require the sender to provide an explicit list of all destinations (e.g., IP addresses). When this method is used, the parameter in the call to send that specifies the destination is a pointer to a list of addresses. This method has the serious drawback that it forces user processes (i.e., the group members) to be aware of precisely who is a member of which group. In other words, it is not transparent. Furthermore, whenever group membership changes, the user processes must update their membership lists. In Fig. 2-33, this administration can easily be done by the kernels to hide it from the user processes.

Group communication also allows a third, and quite novel method of addressing as well, which we will call predicate addressing. With this system, each message is sent to all members of the group (or possibly the entire system) using one of the methods described above, but with a new twist. Each message contains a predicate (Boolean expression) to be evaluated. The predicate can involve the receiver's machine number, its local variables, or other factors. If the predicate evaluates to TRUE, the message is accepted. If it evaluates to FALSE, the message is discarded. Using this scheme it is possible, for example, to send a message to only those machines that have at least 4M of free memory and which are willing to take on a new process.

Ideally, point-to-point and group communication should be merged into a single set of primitives. However, if RPC is the usual user communication mechanism, rather than raw send and receive, it is hard to merge RPC and group communication. Sending a message to a group cannot be modeled as a procedure call. The primary difficulty is that with RPC, the client sends one message to the server and gets back one answer. With group communication there are potentially n different replies. How can a procedure call deal with n replies? Consequently, a common approach is to abandon the (two-way) request/reply model underlying RPC and go back to explicit calls for sending and receiving (one-way model).

The library procedures that processes call to invoke group communication may be the same as for point-to-point communication or they may be different. If the system is based on RPC, user processes never call send and receive directly anyway, so there is less incentive to merge the point-to-point and group primitives. If user programs directly call send and receive themselves, there is something to be said for doing group communication with these existing primitives instead of inventing a new set.

Suppose, for the moment, that we wish to merge the two forms of communication. To send a message, one of the parameters of send indicates the destination. If it is a process address, a single message is sent to that one process. If it is a group address (or a pointer to a list of destinations), a message is sent to all members of the group. A second parameter to send points to the message.

The call can be buffered or unbuffered, blocking or nonblocking, reliable or not reliable, for both the point-to-point and group cases. Generally, these choices are made by the system designers and are fixed, rather than being selectable on a per message basis. Introducing group communication does not change this.

Similarly, receive indicates a willingness to accept a message, and possibly blocks until one is available. If the two forms of communication are merged, receive completes when either a point-to-point message or a group message arrives. However, since these two forms of communication are frequently used for different purposes, some systems introduce new library procedures, say, group_send and group_receive, so a process can indicate whether it wants a point-to-point or a group message.

In the design just described, communication is one-way. Replies are independent messages in their own right and are not associated with previous requests. Sometimes this association is desirable, to try to achieve more of the RPC flavor. In this case, after sending a message, a process is required to call getreply repeatedly to collect all the replies, one at a time.

A characteristic of group communication that we have alluded to several times is the all-or-nothing property. Most group communication systems are designed so that when a message is sent to a group, it will either arrive correctly at all members of the group, or at none of them. Situations in which some members receive a message and others do not are not permitted. The property of all-or-nothing delivery is called atomicity or atomic broadcast.

Atomicity is desirable because it makes programming distributed systems much easier. When any process sends a message to the group, it does not have to worry about what to do if some of them do not get it. For example, in a replicated distributed data base system, suppose that a process sends a message to all the data base machines to create a new record in the data base, and later sends a second message to update it. If some of the members miss the message creating the record, they will not be able to perform the update and the data base will become inconsistent. Life is just a lot simpler if the system guarantees that every message is delivered to all the members of the group, or if that is not possible, that it is not delivered to any, and that failure is reported back to the sender so it can take appropriate action to recover.

Implementing atomic broadcast is not quite as simple as it looks. The method of Fig. 2-33 fails because receiver overrun is possible at one or more machines. The only way to be sure that every destination receives every message is to require them to send back an acknowledgement upon message receipt. As long as machines never crash, this method will do.

However, many distributed systems aim at fault tolerance, so for them it is essential that atomicity also holds even in the presence of machine failures. In this light, all the methods of Fig. 2-33 are inadequate because some of the initial messages might not arrive due to receiver overrun, followed by the sender's crashing. Under these circumstances, some members of the group will have received the message and others will not have, precisely the situation that is unacceptable. Worse yet, the group members that have not received the message do not even know they are missing anything, so they cannot ask for a retransmission. Finally, with the sender now down, even if they did know, there is no one to provide the message.

Nevertheless, there is hope. Here is a simple algorithm that demonstrates that atomic broadcast is at least possible. The sender starts out by sending a message to all members of the group. Timers are set and retransmissions sent where necessary. When a process receives a message, if it has not yet seen this particular message, it, too, sends the message to all members of the group (again with timers and retransmissions if necessary). If it has already seen the message, this step is not necessary and the message is discarded. No matter how many machines crash or how many packets are lost, eventually all the surviving processes will get the message. Later we will describe more efficient algorithms for ensuring atomicity.

To make group communication easy to understand and use, two properties are required. The first one is atomic broadcast, as discussed above. It ensures that a message sent to the group arrives at either all members or at none of them. The second property concerns message ordering. To see what the issue is here, consider Fig. 2-34, in which we have five machines, each with one process. Processes 0, 1, 3, and 4 belong to the same group. Processes 0 and 4 want to send a message to the group simultaneously. Assume that multicasting and broadcasting are not available, so that each process has to send three separate (unicast) messages. Process 0 sends to 1, 3, and 4; process 4 sends to 0, 1, and 3. These six messages are shown interleaved in time in Fig. 2-34(a).

The trouble is that when two processes are contending for access to a LAN, the order in which the messages are sent is nondeterministic. In Fig. 2-34(a) we see that (by accident), process 0 has won the first round and sends to process 1. Then process 4 wins three rounds in a row and sends to processes 0, 1, and 3. Finally, process 0 gets to send to 3 and 4. The order of these six messages is shown in different ways in the two parts of Fig. 2-34.

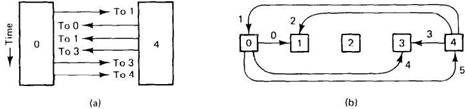
Fig. 2-34. (a) The three messages sent by processes 0 and 4 are interleaved in time. (b) Graphical representation of the six messages, showing the arrival order.

Now consider the situation as viewed by processes 1 and 3 as shown in Fig. 2-34(b). Process 1 first receives a message from 0, then immediately afterward it receives one from 4. Process 3 does not receive anything initially, then it receives messages from 4 and 0, in that order. Thus the two messages arrive in a different order. If processes 0 and 4 are both trying to update the same record in a data base, 1 and 3 end up with different final values. Needless to say, this situation is just as bad as one in which a (true hardware multicast) message sent to the group arrives at some members and not at others (atomicity failure). Thus to make programming reasonable, a system has to have well-defined semantics with respect to the order in which messages are delivered.

The best guarantee is to have all messages delivered instantaneously and in the order in which they were sent. If process 0 sends message A and then slightly later, process 4 sends message B, the system should first deliver A to all members of the group, and then deliver B to all members of the group. That way, all recipients get all messages in exactly the same order. This delivery pattern is something that programmers can understand and base their software on. We will call this global time ordering, since it delivers all messages in the exact order in which they were sent (conveniently ignoring the fact that according to Einstein's special theory of relativity there is no such thing as absolute global time).

Absolute time ordering is not always easy to implement, so some systems offer various watered-down variations. One of these is consistent time ordering, in which if two messages, say A and B, are sent close together in time, the system picks one of them as being "first" and delivers it to all group members, followed by the other. It may happen that the one chosen as first was not really first, but since no one knows this, the argument goes, system behavior should not depend on it. In effect, messages are guaranteed to arrive at all group members in the same order, but that order may not be the real order in which they were sent.

Even weaker time orderings have been used. We will study one of these, based on the idea of causality, when we come to ISIS later in this chapter.

As we mentioned earlier, a process can be a member of multiple groups at the same time. This fact can lead to a new kind of inconsistency. To see the problem, look at Fig. 2-35, which shows two groups, 1 and 2. Processes A, B, and C are members of group 1. Processes B, C, and D are members of group 2.

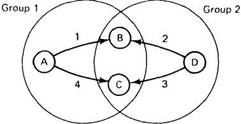
Fig. 2-35. Four processes, A, B, C, and D, and four messages. Processes B and C get the messages from A and D in a different order.

Now suppose that processes A and D each decide simultaneously to send a message to their respective groups, and that the system uses global time ordering within each group. As in our previous example, unicasting is used. The message order is shown in Fig. 2-35 by the numbers 1 through 4. Again we have the situation where two processes, in this case B and C, receive messages in a different order. B first gets a message from A followed by a message from D. C gets them in the opposite order.

The culprit here is that although there is a global time ordering within each group, there is not necessarily any coordination among multiple groups. Some systems support well-defined time ordering among overlapping groups and others do not. (If the groups are disjoint, the issue does not arise.) Implementing time ordering among different groups is frequently difficult to do, so the question arises as to whether it is worth it.

Our final design issue is scalability. Many algorithms work fine as long as all the groups only have a few members, but what happens when there are tens, hundreds, or even thousands of members per group? Or thousands of groups? Also, what happens when the system is so large that it no longer fits on a single LAN, so multiple LANs and gateways are required? And what happens when the groups are spread over several continents?

The presence of gateways can affect many properties of the implementation. To start with, multicasting becomes more complicated. Consider, for example, the internetwork shown in Fig. 2-36. It consists of four LANs and four gateways, to provide protection against the failure of any gateway.

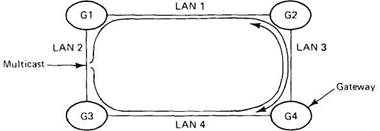
Fig. 2-36. Multicasting in an internetwork causes trouble.

Imagine that one of the machines on LAN 2 issues a multicast. When the multicast packet arrives at gateways G1 and G3, what should they do? If they discard it, most of the machines will never see it, destroying its value as a multicast. If, however, the algorithm is just to have gateways forward all multicasts, then the packet will be copied to LAN 1 and LAN 4, and shortly thereafter to LAN 3 twice. Worse yet, gateway G2 will see G4 's multicast and copy it to LAN 2, and vice versa. Clearly, a more sophisticated algorithm involving keeping track of previous packets is required to avoid exponential growth in the number of packets multicast.

Another problem with an internetwork is that some methods of group communication take advantage of the fact that only one packet can be on a LAN at any instant. In effect, the order of packet transmission defines an absolute global time order, which as we have seen, is frequently crucial. With gateways and multiple networks, it is possible for two packets to be "on the wire" simultaneously, thus destroying this useful property.

Finally, some algorithms may not scale well due to their computational complexity, their use of centralized components, or other factors.

Оглавление книги