Книга: Distributed operating systems

6.6.2. Linda

6.6.2. Linda

Linda provides processes on multiple machines with a highly structured distributed shared memory. This memory is accessed through a small set of primitive operations that can be added to existing languages, such as C and FORTRAN to form parallel languages, in this case, C-Linda and FORTRAN-Linda. In the description below, we will focus on C-Linda, but conceptually the differences between the variants are small. More information about Linda can be found in (Carriero and Gelernter, 1986, 1989; and Gelernter, 1985).

This approach has several advantages over a new language. A major advantage is that users do not have to learn a new language. This advantage should not be underestimated. A second one is simplicity: turning a language, X, into X-Linda can be done by adding a few primitives to the library and adapting the Linda preprocessor that feeds Linda programs to the compiler. Finally, the Linda system is highly portable across operating systems and machine architectures and has been implemented on many distributed and parallel systems.

The unifying concept behind Linda is that of an abstract tuple space. The tuple space is global to the entire system, and processes on any machine can insert tuples into the tuple space or remove tuples from the tuple space without regard to how or where they are stored. To the user, the tuple space looks like a big, global shared memory, as we saw in Fig. 6-35. The actual implementation may involve multiple servers on multiple machines, and will be described later.

A tuple is like a structure in C or a record in Pascal. It consists of one or more fields, each of which is a value of some type supported by the base language. For C-Linda, field types include integers, long integers, and floatingpoint numbers, as well as composite types such as arrays (including strings) and structures, (but not other tuples). Figure 6-36 shows three tuples as examples.

("abc", 2, 5)
("matrix-1", 1,6,3.14)
("family", "is-sister", "Carolyn", "Elinor")

Fig. 6-36. Three Linda tuples.

Linda is not a fully general object-based system since it provides only a fixed number of built-in operations and no way to define new ones. Four operations are provided on tuples. The first one, out, puts a tuple into the tuple space. For example,

out("abc", 2, 5);

puts the tuple ("abc", 2, 5) into the tuple space. The fields of out are normally constants, variables, or expressions, as in

out("matrix-l", i, j, 3.14);

which outputs a tuple with four fields, the second and third of which are determined by the current values of the variables i and j.

Tuples are retrieved from the tuple space by the in primitive. They are addressed by content rather than by name or address. The fields of in can be expressions or formal parameters. Consider, for example,

in("abc", 2, ? i);

This operation "searches" the tuple space for a tuple consisting of the string "abc", the integer, 2, and a third field containing any integer (assuming that i is an integer). If found, the tuple is removed from the tuple space and the variable i is assigned the value of the third field. The matching and removal are atomic, so if two processes execute the same in operation simultaneously, only one of them will succeed, unless two or more matching tuples are present. The tuple space may even contain multiple copies of the same tuple.

The matching algorithm used by in is straightforward. The fields of the in primitive, called the template, are (conceptually) compared to the corresponding fields of every tuple in the tuple space. A match occurs if the following three conditions are all met:

1. The template and the tuple have the same number of fields.

2. The types of the corresponding fields are equal.

3. Each constant or variable in the template matches its tuple field.

Formal parameters, indicated by a question mark followed by a variable name or type, do not participate in the matching (except for type checking), although those containing a variable name are assigned after a successful match.

If no matching tuple is present, the calling process is suspended until another process inserts the needed tuple, at which time the caller is automatically revived and given the new tuple. The fact that processes block and unblock automatically means that if one process is about to output a tuple and another is about to input it, it does not matter which goes first. The only difference is that if the in is done before the out, there will be a slight delay until the tuple is available for removal.

The fact that processes block when a needed tuple is not present can be put to many uses. For example, it can be used to implement semaphores. To create or do an UP(V) on semaphore S, a process can execute

out("semaphore S");

To do a DOWN(P), it does

in("semaphore S");

The state of semaphore S is determined by the number of ("semaphore S") tuples in the tuple space. If none exist, any attempt to get one will block until some other process supplies one.

In addition to out and in, Linda also has a primitive read, which is the same as in except that it does not remove the tuple from the tuple space. There is also a primitive eval, which causes its parameters to be evaluated in parallel and the resulting tuple to be deposited in the tuple space. This mechanism can be used to perform an arbitrary computation. This is how parallel processes are created in Linda.

A common programming paradigm in Linda is the replicated worker model. This model is based on the idea of a task bag full of jobs to be done. the main process starts out by executing a loop containing

out("task-bag", job);

in which a different job description is output to the tuple space on each iteration. Each worker starts out by getting a job description tuple using

in("task-bag", ?job);

which it then carries out. When it is done, it gets another. New work may also be put into the task bag during execution. In this simple way, work is dynamically divided among the workers, and each worker is kept busy all the time, all with little overhead.

In certain ways, Linda is similar to Prolog, on which it is loosely based. Both support an abstract space that functions as a kind of data base. In Prolog, the space holds facts and rules; in Linda it holds tuples. In both cases, processes can provide templates to be matched against the contents of the data base.

Despite these similarities, the two systems also differ in significant ways. Prolog was intended for programming artificial intelligence applications on a single processor, whereas Linda was intended for general programming on multicomputers. Prolog has a complex pattern-matching scheme involving unification and backtracking; Linda's matching algorithm is much simpler. In Linda, a successful match removes the matching tuple from the tuple space; in Prolog it does not. Finally, a Linda process unable to locate a needed tuple blocks, which forms the basis for interprocess synchronization. In Prolog, there are no processes and programs never block.

Efficient implementations of Linda are possible on various kinds of hardware. Below we will discuss some of the more interesting ones. For all implementations, a preprocessor scans the Linda program, extracting useful information and converting it to the base language where need be (e.g., the string "? int" is not allowed as a parameter in C or FORTRAN). The actual work of inserting and removing tuples from the tuple space is done during execution by the Linda runtime system.

An efficient Linda implementation has to solve two problems:

1. How to simulate associative addressing without massive searching.

2. How to distribute tuples among machines and locate them later.

The key to both problems is to observe that each tuple has a type signature, consisting of the (ordered) list of the types of its fields. Furthermore, by convention, the first field of each tuple is normally a string that effectively partitions the tuple space into disjoint subspaces named by the string. Splitting the tuple space into subspaces, each of whose tuples has the same type signature and same first field, simplifies programming and makes certain optimizations possible.

For example, if the first parameter to an in or out call is a literal string, it is possible to determine at compile time which subspace the call operates on. If the first parameter is a variable, the determination is made at run time. In both cases, this partitioning means that only a fraction of the tuple space has to be searched. Figure 6-37 shows four tuples and four templates. Together they form four subspaces. For each out or in, it is possible to determine at compile time which subspace and tuple server are needed. If the initial string was a variable, the determination of the correct subspace would have to be delayed until run time.

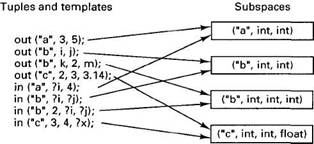
Fig. 6-37. Tuples and templates can be associated with subspaces.

In addition, each subspace can be organized as a hash table using its i th tuple field as the hash key. If field i is a constant or variable (but not a formal parameter), an in or out can be executed by computing the hash function of the i th field to find the position in the table where the tuple belongs. Knowing the subspace and table position eliminates all searching. If the i th field of a certain in is a formal parameter, hashing is not possible, so a complete search of the subspace is needed except in some special cases. By carefully choosing the field to hash on, however, the preprocessor can usually avoid searching most of the time. Other subspace organizations beside hashing are also possible for special cases (e.g., a queue when there is one writer and one reader).

Additional optimizations are also used. For example, the hashing scheme described above distributes the tuples of a given subspace into bins, to restrict searching to a single bin. It is possible to place different bins on different machines, both to spread the load more widely and to take advantage of locality. If the hashing function is the key modulo the number of machines, the number of bins scales linearly with the system size. 

Now let us examine various implementation techniques for different kinds of hardware. On a multiprocessor, the tuple subspaces can be implemented as hash tables in global memory, one for each subspace. When an in or an out is performed, the corresponding subspace is locked, the tuple entered or removed, and the subspace unlocked.

On a multicomputer, the best choice depends on the communication architecture. If reliable broadcasting is available, a serious candidate is to replicate all the subspaces in full on all machines, as shown in Fig. 6-38. When an out is done, the new tuple is broadcast and entered into the appropriate subspace on each machine. To do an in, the local subspace is searched. However, since successful completion of an in requires removing the tuple from the tuple space, a delete protocol is required to remove it from all machines. To prevent races and deadlocks, a two-phase commit protocol can be used.

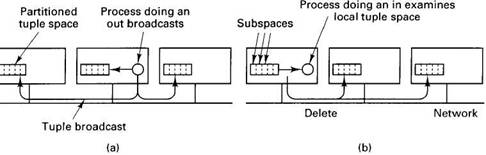
Fig. 6-38. Tuple space can be replicated on all machines. The dotted lines show the partitioning of the tuple space into subspaces. (a) Tuples are broadcast on out. (b). Ins are local, but the deletes must be broadcast.

This design is straightforward, but may not scale well as the system grows in size, since every tuple must be stored on every machine. On the other hand, the total size of the tuple space is often quite modest, so problems may not arise except in huge systems. The S/Net Linda system uses this approach because S/Net has a fast, reliable, word-parallel bus broadcast (Carriero and Gelernter, 1986).

The inverse design is to do outs locally, storing the tuple only on the machine that generated it, as shown in Fig. 6-39. To do an in, a process must broadcast the template. Each recipient then checks to see if it has a match, sending back a reply if it does. 

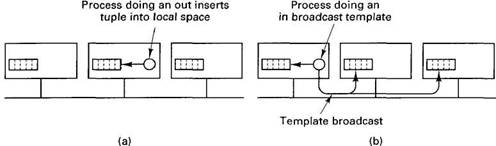
Fig. 6-39. Unreplicated tuple space. (a) An out is done locally. (b) An in requires the template to be broadcast in order to find a tuple.

If the tuple is not present, or if the broadcast is not received at the machine holding the tuple, the requesting machine retransmits the broadcast request ad infinitem, increasing the interval between broadcasts until a suitable tuple materializes and the request can be satisfied. If two or more tuples are sent, they are treated like local outs and the tuples are effectively moved from the machines that had them to the one doing the request. In fact, the runtime system can even move tuples around on its own to balance the load. Carriero et al. (1986) used this method for implementing Linda on a LAN.

These two methods can be combined to produce a system with partial replication. A simple example is to imagine all the machines logically forming a rectangle, as shown in Fig. 6-40. When a process on a machine, A, wants to do an out, it broadcasts (or sends by point-to-point message) the tuple to all machines in its row of the matrix. When a process on a machine, B, wants to do an in it broadcasts the template to all machines in its column. Due to the geometry, there will always be exactly one machine that sees both the tuple and the template (C in this example), and that machine makes the match and sends the tuple to the process asking for it. Krishnaswamy (1991) used this method for a hardware Linda coprocessor.

Finally, let us consider the implementation of Linda on systems that have no broadcast capability at all (Bjornson, 1993). The basic idea is to partition the tuple space into disjoint subspaces, first by creating a partition for each type signature, then by dividing each of these partitions again based on the first field. Potentially, each of the resulting partitions can go on a different machine, handled by its own tuple server, to spread the load around. When either an out or an in is done, the required partition is determined, and a single message is sent to that machine either to deposit a tuple there or to retrieve one.

Experience with Linda shows that distributed shared memory can be handled in a radically different way than moving whole pages around, as in the page-based systems we studied above. It is also quite different from sharing variables with release or entry consistency. As future systems become larger and more powerful, novel approaches such as this may lead to new insights into how to program these systems in an easier way. 

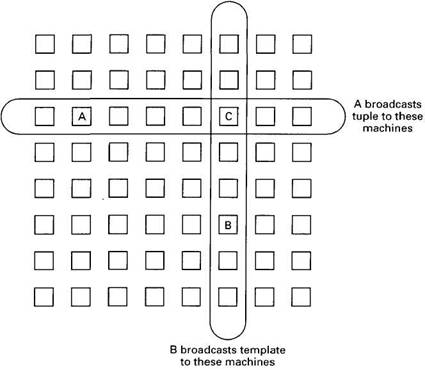
Fig. 6-40. Partial broadcasting of tuples and templates.

Оглавление книги