Книга: Кибернетика или управление и связь в животном и машине

Глава II. Группы и статистическая механика

Глава II. Группы и статистическая механика

К началу этого столетия двое ученых, один в Соединенных Штатах, другой во Франции, работали в областях, которые показались бы им совершенно не связанными, если бы один из них узнал о существовании другого. Уиллард Гиббс в Нью-Хейвене разрабатывал свой новый подход к статистической механике. Анри Лебег в Париже соперничал славой со своим учителем Эмилем Борелем, создав новую, более мощную теорию интегрирования, которая должна была использоваться при изучении тригонометрических рядов. Эти два исследователя походили друг на друга тем, что оба были кабинетными, а не лабораторными работниками, но они подходили к науке с диаметрально противоположных позиций.

Гиббс, хотя и был математиком, всегда считал математику наукой, подчиненной физике. Лебег был чистейший аналитик, выдающийся представитель современных, крайне суровых требований к математической строгости, и его работы, насколько мне известно, не содержат ни одного примера задач или методов, вытекающих непосредственно из физики. Тем не менее работы этих ученых составляют единое целое, и на вопросы, которые ставит Гиббс, мы находим ответ не в его собственных работах, а в работах Лебега.

Главная мысль Гиббса такова. В ньютоновой динамике в ее первоначальном виде рассматривается индивидуальная система с заданными начальными скоростями и импульсами[125], подвергающаяся изменениям под [c.100] действием некоторой системы сил согласно законам Ньютона, которые устанавливают связь между силой и ускорением. Однако в громадном большинстве практических случаев нам известны далеко не все начальные скорости и импульсы. Если принять некоторое начальное распределение не вполне известных положений и импульсов системы, то тем самым будет определено в строго ньютоновском смысле распределение положений и импульсов в любой момент будущего. Тогда можно высказать ряд предложений об этих распределениях, и часть из них — в форме утверждений, что система будет иметь некоторые характеристики с вероятностью 1 и некоторые другие — с вероятностью 0.

Вероятности, равные единице и нулю, суть понятия, включающие полную достоверность и полную невозможность, но их значение гораздо шире. Если я стреляю по цели нулей точечного размера, то вероятность моего попадания в определенную точку цели равна нулю, хотя не исключена возможность, что я попаду в нее; и, действительно, в каждом отдельном случае я обязательно попаду в некоторую точку, что является событием нулевой вероятности. Таким образом, событие вероятности 1, а именно попадание в какую-либо точку, может состоять из совокупности событий, каждое из которых имеет вероятность 0.

Тем не менее в гиббсовой статистической механике применяется, хотя и неявно (Гиббс нигде не отдает себе в этом ясного отчета), разложение сложного события в бесконечную последовательность частных событий — первого, второго, третьего и т. д., — каждое из которых имеет известную вероятность; вероятность этого более широкого события находится затем как сумма вероятностей частных событий, образующих бесконечную последовательность. Таким образом, вероятности нельзя складывать во всех мыслимых случаях для получения полной вероятности, ибо сумма любого числа нулей равна нулю; но их можно складывать, коль скоро существует первый, второй, третий член и т. д., образующие последовательность событий, в которой каждый член имеет определенное место, задаваемое положительным целым числом.

Чтобы провести различие между этими двумя случаями, необходимы довольно тонкие изыскания о природе [c.101] множеств событий, а Гиббс был хотя и очень сильный, но не очень тонкий математик. Может ли класс быть бесконечным и в то же время существенно отличным по мощности от другого класса, например от класса натуральных чисел? Эту задачу решил в конце прошлого столетия Георг Кантор, и ответ был «да». Если мы рассмотрим все десятичные дроби, конечные и бесконечные, лежащие между нулем и единицей, то, как известно, их нельзя расположить в порядке «один, два, три…», хотя — удивительно — мы можем расположить так все конечные десятичные дроби. Поэтому проведение различия, требуемого в статистической механике Гиббса, не является само по себе невозможным. Услуга, оказанная Лебегом теории Гиббса, заключалась в доказательстве того, что неявные требования статистической механики относительно событий нулевой вероятности и сложения вероятностей событий действительно могут быть удовлетворены и что теория Гиббса не содержит противоречий.

Однако работа Лебега была непосредственно связана не с требованиями статистической механики, а с другой, как будто весьма далекой от нее, теорией — теорией тригонометрических рядов. Последняя восходит к физике XVIII в., изучавшей волны и колебания, и к спорному тогда вопросу об общности возможных движений линейной системы, полученных сложением ее простых колебаний, — колебаний, при которых течение времени лишь умножает отклонения системы от равновесия на положительный или отрицательный множитель, зависящий только от времени, но не от положения. Таким образом, одна функция выражается в виде суммы ряда. Коэффициенты этих рядов выражаются как средние произведения представляемой функции на данную весовую функцию. Вся теория основана на соотношениях между средним значением ряда и средними значениями отдельных членов. Заметим, что среднее значение величины, равной единице на интервале от нуля до А и нулю на интервале от А до 1, равно А и что его можно рассматривать как вероятность для случайной точки находиться в интервале от 0 до А, если известно, что она находится между 0 и 1. Иными словами, теория, необходимая для определения среднего значения ряда, очень близка к той, которая необходима для [c.102] адекватной трактовки вероятностей, выводимых из бесконечной последовательности случаев. Вот почему Лебег, решая свою задачу, решил также задачу Гиббса.

Распределения, исследуемые Гиббсом, сами допускают динамическую интерпретацию. Если мы рассматриваем консервативную динамическую систему весьма общего вида с N степенями свободы, то координаты положений и скоростей такой системы можно привести к особой системе 2N координат, из которых N называются обобщенными координатами положения и N — обобщенными импульсами. Эти координаты определяют 2N-мерное пространство[126] и в нем 2N-мерный объем. Возьмем произвольную область этого пространства и заставим точки перемещаться с течением времени. Каждый набор 2N координат перейдет тогда в новый набор, зависящий от истекшего времени, но непрерывное изменение границ области не изменит ее 2N-мерного объема. В общем случае для множеств, не столь простых, понятие объема порождает систему меры лебегова типа. В этой системе меры и в консервативных динамических системах, преобразуемых так, что мера сохраняется постоянной, сохраняет постоянство и другая скалярная величина — энергия. Если все тела системы действуют только друг на друга и в системе нет сил, связанных с фиксированным положениями и фиксированными направлениями в пространстве, то остаются постоянными еще два выражения, оба векторные: количество движения и момент количества движения системы в целом. Их нетрудно исключить и тем самым заменить данную систему системой с меньшим числом степеней свободы.

В сугубо частных системах могут быть и другие величины, не определяемые энергией, количеством движения и моментом количества движения, также не меняющиеся с эволюцией системы. Известно, однако, что системы с другими инвариантными величинами, зависящими от начальных координат и импульсов динамической системы и достаточно регулярными, чтобы [c.103] допускать интегрирование на основе меры Лебега, в действительности очень редки, в некотором вполне точном смысле[127]. В системах, не имеющих других инвариантных величин, можно фиксировать координаты, соответствующие энергии, количеству движения и общему моменту количества движения, и тогда в пространстве остальных координат мера, определяемая координатами положений и импульсов, определит сама некоторую подмеру, подобно тому, как мера в трехмерном пространстве определит площадь на двумерной поверхности для заданного семейства двумерных поверхностей. Например, пусть мы имеем семейство концентрических сфер; объем между двумя сближаемыми концентрическими сферами (если его нормировать, приняв за единицу полный объем области между двумя сферами) в пределе даст меру площади на поверхности сферы.

Применим теперь эту новую меру к одной из областей фазового пространства, для которой определена энергия, общее количество движения и общий момент количества движения, и предположим, что в системе нет других измеримых инвариантных величин. Пусть полная мера этой ограниченной области постоянна; изменяя масштаб, ее можно приравнять единице. Поскольку наша мера была получена из меры, инвариантной во времени, способом, инвариантным во времени, она и сама инвариантна. Мы назовем эту меру фазовой мерой, а средние по этой мере — фазовыми средними.

Но всякая величина, изменяющаяся во времени, может иметь также среднее значение по времени — временно?е среднее. Например, если f(t) зависит от t, то временно?е среднее для прошлого равно

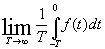
а временно?е среднее для будущего

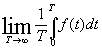
[c.104]

В гиббсовой статистической механике встречаются как временные, так и пространственные средние. Блестящей идеей Гиббса была попытка доказать, что эти средние в некотором смысле тождественны. Догадка Гиббса о связи двух типов средних совершенно правильна, но метод, которым он пытался доказать эту связь, был совершенно и безнадежно неверным. В этом его вряд ли можно винить. Интеграл Лебега стал известен в Америке лишь к моменту смерти Гиббса. В течение еще пятнадцати лет он был музейной редкостью и применялся только, чтобы продемонстрировать молодым математикам, до какой степени могут быть доведены требования математической строгости. Такой выдающийся математик, как У.Ф. Осгуд, не хотел его признать до конца своей жизни[128]. Лишь около 1930 г. группа математиков — Купмен, фон Нейман, Биркгофф[129] — установила наконец прочные основы статистической механики Гиббса. Каковы были эти основы, мы увидим дальше, когда познакомимся с эргодической теорией.

Сам Гиббс думал, что в системе, из которой удалены все инварианты — лишние координаты, почти все пути точек в фазовом пространстве проходят через все координаты такого пространства. Эту гипотезу он назвал эргодической, от греческих слов ????? — «работа» и ???? — «путь». Но как показал Планшерель и другие, ни в одном реальном случае эта гипотеза не оправдывается. Никакая дифференцируемая траектория, даже бесконечной длины, не может покрыть целиком область на плоскости. Последователи Гиббса и, по-видимому, в конце концов сам Гиббс смутно поняли это и заменили свою гипотезу другой, квазиэргодической гипотезой, которая утверждает лишь, что с течением времени система в общем случае проходит неограниченно близко к каждой точке в области фазового пространства определенной известными интервалами. Логически такая гипотеза вполне приемлема, но она совершенно недостаточна для тех выводов, которые Гиббс основывает на ней. Она ничего не говорит об относительном времени пребывания системы в окрестности каждой точки. [c.105]

Помимо понятии среднего и меры (иначе говоря, среднего по всему пространству от функции, равной 1 на измеряемом множестве и 0 вне его), необходимых в первую очередь для разбора идей Гиббса, мы нуждаемся при оценке действительного значения эргодической теории в более точном анализе понятия инварианта, как и понятия группы преобразований. Эти понятия, несомненно, были известны Гиббсу, как показывают его работы по векторному анализу. Тем не менее можно утверждать, что он не оценил в полной мере их философского значения. Подобно своему современнику Хевисайду, Гиббс принадлежал к типу ученых, у которых физико-математическая проницательность часто опережает их логику и которые обыкновенно бывают правы, но часто не в состоянии объяснить, почему и как.

Для существования любой науки необходимо, чтобы существовали явления, которые не оставались бы изолированными. Если бы мир управлялся серией чудес, совершаемых иррациональным богом с его внезапными прихотями, то мы были бы вынуждены ждать каждой новой катастрофы в состоянии пассивного недоумения. Подобную картину мира встречаем мы в крокетной игре, описанной в «Алисе в стране чудес»[130]. В этой игре молотки — фламинго, шары — ежи, которые спокойно разворачиваются и идут по своим делам, ворота — карточные солдаты, точно так же способные совершать движения по собственной инициативе, а правила игры определяются декретами вспыльчивой королевы червей[131], поведение которой невозможно предугадать.

Существо эффективного правила игры или полезного закона физики состоит в том, что правило можно установить заранее и применять во многих случаях. В идеале закон должен описывать свойство рассматриваемой системы, остающееся всегда тем же самым в потоке частных событий. В простейшем случае берется свойство, инвариантное относительно множества преобразований, которым подвергается система. Так мы приходим к [c.106] понятиям преобразования, группы преобразований и инварианта.

Преобразование системы есть изменение, при котором каждый элемент переходит в другой элемент. Изменение Солнечной системы в промежуток между моментами времени t₁ и t₂ есть преобразование координат планет. Аналогичное изменение их координат при перемещении нами начала координат или повороте наших геометрических осей также есть преобразование. Изменение масштаба, происходящее, когда мы наблюдаем препарат в микроскоп, — еще один пример преобразования.

Если за преобразованием А следует преобразование В, то в результате получается преобразование, называемое произведением, или результирующим преобразованием ВА. Заметим, что произведение, вообще говоря, зависит от порядка преобразований A и В. Например, если А — преобразование, переводящее координату х в координату y, а у — в х, оставляя z без изменений, и если В переводит х в z, а z — в х, оставляя y без изменений, то ВА будет переводить х в у, у — в z и z — в х, а АВ будет переводить х в z, у — в х и z — в у. Если АВ и ВА совпадают, то говорят, что А и В перестановочны.

Иногда, но не всегда, преобразование А не только переводит каждый элемент системы в элемент, но обладает еще тем свойством, что каждый элемент оказывается результатом преобразования одного из элементов. В этом случае существует такое единственное преобразование А^—1, что каждое из произведений АА^—1 и А^—1A представляет собой особое, вырожденное преобразование, которое называется тождественным преобразованием I и преобразует каждый элемент в самого себя. В этом случае мы называем преобразование А^—1 обратным к преобразованию А. Очевидно, что А обратно к А^—1, что I обратно к самому себе и что обратное преобразование к АВ есть B^—1A^—1.

Существуют множества преобразований, в которых: 1) каждое преобразование, принадлежащее к данному множеству, имеет обратное преобразование, также принадлежащее к этому множеству, и 2) произведение любых двух преобразований, принадлежащих к данному множеству, само принадлежит к этому множеству. Такие множества носят название групп преобразований. [c.107] Множество всех сдвигов или по прямой, или в плоскости, или в трехмерном пространстве есть группа преобразований; более того, оно принадлежит к группам преобразований особого рода, называемым абелевыми группами[132], где любые два преобразования перестановочны. Напротив, множество поворотов около точки и множество всех перемещений твердого тела в пространстве суть неабелевы группы.

Предположим теперь, что имеется какая-то величина, связанная со всеми элементами, преобразуемыми данной группой преобразований. Если эта величина не изменяется, когда каждый элемент изменяется одним и тем же преобразованием группы, каково бы ни было это преобразование, то она называется инвариантом группы. Существует много разновидностей таких инвариантов. Из них для наших целей особенно важны две.

Первая разновидность — так называемые линейные инварианты. Обозначим через х элементы, преобразуемые абелевой группой, и пусть f(x) — комплексная функция этих элементов, обладающая надлежащими свойствами непрерывности или интегрируемости. Тогда, если Тх — элемент, получаемый из х при преобразовании Т, a f(x) — функция с абсолютным значением 1, такая, что

f (Tx) = ?(T) f(x),          (2.03)

где ?(T) — число с абсолютным значением 1, зависящее только от Т, то f(x) мы будем называть характером группы.

Это инвариант группы в несколько обобщенном смысле. Ясно, что если f(x) и g(x) — характеры группы, то f(x)g(x) также есть характер группы, как и [f(x)] ^—1. Если какая-либо функция h(x), определенная на группе, представима линейной комбинацией характеров группы, скажем в виде

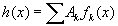
где f_k(x) — характер группы, и если ?_k(T) находится в таком же отношении к f_k(x), как ?(T) — к f(x) в (2.03), то [c.108]

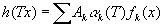
Таким образом, коль скоро h(x) допускает разложение по некоторому множеству характеров группы, то и h(Tx) при всех Т допускает такое разложение.

Мы видели, что характеры группы порождают другие характеры при умножении и обращении; нетрудно видеть также, что константа 1 есть характер. Следовательно, умножение на характер порождает группу преобразований самих характеров; последняя называется группой характеров исходной группы.

Если исходная группа есть группа сдвигов по бесконечной прямой, то оператор Т изменяет х в х+Т и соотношение (2.03) переходит в соотношение

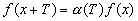
которое выполняется при f(x)=e^i?x, ?(T)= e^i?T. Характерами будут функции e^i?x, а группой характеров будет группа сдвигов, изменяющая ? в ?+? и, следовательно, имеющая такое же строение, как и исходная группа. Но дело будет обстоять иначе, если исходная группа состоит из поворотов по окружности. В этом случае оператор Т изменяет х в число, лежащее между 0 и 2? и отличающееся от х+Т на целочисленное кратное 2?. Соотношение (2.06) еще справедливо, но у нас появляется добавочное условие

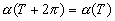
Положив вновь f(x) = e^i?x, получим

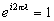
Это значит, что ? должно быть целым действительным числом — положительным, отрицательным или нулем. Следовательно, группа характеров здесь соответствует сдвигам целых действительных чисел. С другой стороны, если исходная группа есть группа сдвигов целых чисел, то х и Т в (2.06) могут принимать только целочисленные значения и функция e^i?x задается полностью числом, лежащим между 0 и 2? и отличающимся от ? на целочисленное кратное 2?. Следовательно, группа характеров в этом случае по существу представляет собой группу поворотов по окружности.

В любой группе характеров числа ?(T), соответствующие данному характеру f, распределены таким образом, [c.109] что это распределение не нарушается при умножении их всех на ?(S), каков бы ни был элемент S исходной группы. Иначе говоря, если есть какое-то разумное основание взять среднее от этих чисел, не затрагиваемое, когда группа преобразуется умножением каждого ее преобразования на одно фиксированное, то либо ?(Т) тождественно равно 1, либо наше среднее инвариантно относительно умножения на числа, отличные от 1, и потому должно равняться 0. Отсюда можно заключить, что среднее произведение характера на величину, с ним сопряженную (которая также является характером), будет равно 1, а среднее произведение характера на величину, сопряженную с другим характером, будет равно 0. Другими словами, если h(x) представлено как в (2.04), то

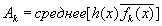
Для группы поворотов по окружности это дает нам сразу, что если

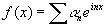
то

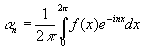
Для сдвигов же по бесконечной прямой результат тесно связан с тем обстоятельством, что если в некотором подходящем смысле

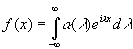
то в определенном смысле

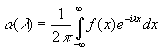
Эти результаты изложены здесь очень грубо, без точной формулировки условий их справедливости. Более строгое изложение теории читатель может найти в работе, указанной в примечании[133]. [c.110]

Наряду с теорией линейных инвариантов группы, существует также общая теория ее метрических инвариантов. Последние представляют собой системы меры Лебега, не претерпевающие изменений, когда объекты, преобразуемые группой, переставляются операторами группы. В этой связи следует упомянуть интересную теорию групповой меры, которую дал Гаар[134]. Как мы видели, всякая группа сама есть собрание объектов, которые переставляются между собой при умножении на операторы данной группы. Поэтому она может иметь инвариантную меру. Гаар доказал, что некоторый довольно широкий класс групп имеет однозначно определенную инвариантную меру, задаваемую строением самой группы.

Наиболее важное применение теории метрических инвариантов группы преобразований состоит в обосновании взаимной заменимости фазовых и временных средних, которую, как мы видели выше, Гиббс тщетно пытался доказать. Это доказательство было выполнено на основе так называемой эргодической теории.

В обычных эргодических теоремах рассматривается ансамбль Е, меру которого можно принять за единицу, и этот ансамбль преобразуется в себя сохраняющим меру преобразованием Т или группой сохраняющих меру преобразований Т^?, где —?<?<? и

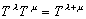
Эргодическая теория имеет дело с комплексным функциями f(х) элементов х из Е. Во всех случаях f(х) считается измеримой по х, а если мы рассматриваем непрерывную группу преобразований, то f(Т^?х) считается измеримой по х и ? вместе.

В эргодической теореме Купмена — фон Неймана о сходимости в среднем функция f(х) считается принадлежащей к классу L²; это значит, что

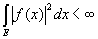
Теорема утверждает, что [c.111]

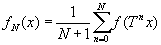
или соответственно

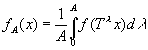
сходится в среднем к пределу f^*(х) при N?? или соответственно при А?? в том смысле, что

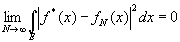
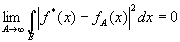
В эргодической теореме Биркгоффа о сходимости «почти всюду» функция f(х) считается принадлежащей к классу L; это значит, что

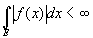
Функции fN(х) и f_A(х) определяются, как в (2.16) и (2.17). Теорема утверждает[135], что для всех значений х, за исключением множества нулевой меры, существуют пределы

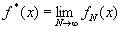
и

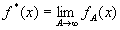
Особенно интересен так называемый эргодический, или метрически транзитивный, случай, когда преобразование Т или множество преобразований Т^? не оставляет инвариантным ни одно множество точек х с мерой, отличной от 1 и 0. В таком случае множество значений (для обеих эргодических теорем), на которых f^*(х) пробегает заданный интервал, почти всегда есть 1 или 0. Это возможно только при том условии, что [c.112] f^*(х) почти всегда постоянна. Тогда f^*(х) почти всегда равна

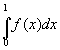
Таким образом, в теореме Купмена мы получаем предел в среднем[136]

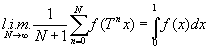
а в теореме Биркгоффа

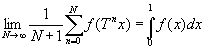
за исключением множества значений х меры (или вероятности) 0. Аналогичные результаты имеют место в непрерывном случае. Это служит достаточным обоснованием производимой Гиббсом замены фазовых и временных средних.

Для случая, когда преобразование Т или группа преобразований Т^? не являются эргодическими, фон Нейман показал, что при очень общих условиях они могут быть сведены к эргодическим составляющим. Это значит, что, отбросив множество значений х нулевой меры, Е можно разбить на конечное или счетное множество классов Еn и континуум классов Е(y), таких, что на каждом Еn и Е(y) устанавливается мера, инвариантная при Т и Т^?. Все эти преобразования эргодические, и если S(y) — пересечение множества S с Е(y), Sn — пересечение множества S с Еn, то

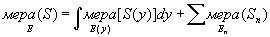
Другими словами, вся теория сохраняющих меру преобразований может быть сведена к теории эргодических преобразований.

Заметим мимоходом, что вся эргодическая теория применима и к более общим группам преобразований, [c.113] чем те, которые изоморфны с группой сдвигов по прямой. В частности, ее можно применить к группе сдвигов в n измерениях. Для физики важен случай трех измерений. Пространственным аналогом равновесия во времени служит пространственная однородность, и такие теории, как теория однородного газа, жидкости или твердого тела, основаны на применении трехмерной эргодической теории. Между прочим, примером неэргодической группы преобразований сдвига в трех изменениях может служить множество сдвигов смеси раздельных состояний, таких, что в данный момент существует то или другое состояние, но не их смесь.

Одним из кардинальных понятий статистической механики, получившим также применение в классической термодинамике, является понятие энтропии. Энтропия — это прежде всего свойство областей фазового пространства; она выражается логарифмом от их меры вероятности. Например, рассмотрим динамику n частиц, находящихся в сосуде, который разделен на две части: А и В. Если m частиц находится в А и n—m в В, то это характеризует некоторую область в фазовом пространстве, имеющую определенную меру вероятности. Логарифм этой меры есть энтропия распределения «m частиц в А, n—m в В». Большую часть времени система будет пребывать в состоянии, близком к состоянию наибольшей энтропии, в том смысле, что если комбинация «m₁ в А, n—m₁ в В» имеет наибольшую вероятность, то большую часть времени примерно m₁ частиц будет в А и примерно n— m₁ в В. Для систем с большим числом частиц и состояниями, еще остающимися в пределах практической различимости, это значит, что если взять состояние с энтропией ниже максимальной и наблюдать, что произойдет, то энтропия почти всегда возрастает.

В обычных термодинамических задачах о тепловом двигателе мы имеем дело с условиями, когда в больших областях, скажем в цилиндре двигателя, существует грубое тепловое равновесие. Состояния, для которых мы исследуем энтропию, уже являются состояниями максимальной энтропии для данной температуры и объема, где речь идет о немногих областях фиксированных объемов и температуры. Даже при более тонких рассмотрениях тепловых двигателей, в частности двигателей [c.114] типа турбины, где газ расширяется гораздо более сложным образом, чем в цилиндре, эти условия не изменяются очень сильно. Мы все еще может говорить с весьма хорошим приближением о местных температурах, хотя температура определима точно лишь в состоянии равновесия и методами, предполагающими такое равновесие. Но в живом веществе мы уже не можем предполагать даже этой грубой однородности. В строении белковой ткани, которое показывает электронный микроскоп, наблюдается чрезвычайная определенность и тонкость организации, и физиология такой ткани должна обладать соответственно тонкой организацией. Эта тонкость гораздо больше, чем у пространственно-временной шкалы обычного термометра, и потому температуры, измеряемые обычными термометрами в живых тканях, представляют грубые средние величины, а не истинные термодинамические температуры. Гиббсова статистическая механика может оказаться довольно адекватной моделью того, что происходит в живом теле; картина, подсказанная обычным тепловым двигателем, — заведомо нет. Тепловой коэффициент полезного действия мышц почти ничего не значит и, уж конечно, он не значит того, что он, казалось бы, должен значить.

Очень важное значение в статистической механике имеет идея максвеллова демона. Представим себе газ, в котором частицы движутся с распределением скоростей, остающимся в статистическом равновесии при данной температуре. Для идеального газа это будет распределение Максвелла. Пусть наш газ заключен в твердый сосуд с поперечной стенкой, снабженной небольшим отверстием; отверстие закрывается дверцей, приводимой в действие привратником — человекоподобным демоном или миниатюрным механизмом. Когда частица со скоростью выше средней подходит к дверце из отделения А или частица со скоростью ниже средней подходит к дверце из отделения В, привратник открывает дверцу и частица проходит через отверстие; когда же частица со скоростью ниже средней подходит из отделения А или частица со скоростью выше средней подходит из отделения В, дверца закрывается. Таким образом, частицы большей скорости сосредоточиваются в отделении В, а в отделении А их концентрация уменьшается. Это вызывает очевидное уменьшение энтропии, [c.115] и если соединить оба отделения тепловым двигателем, мы, как будто, получим вечный двигатель второго рода[137].

Легче отвергнуть вопрос, поставленный Максвеллом, чем ответить на него. Самое простое — отрицать возможность подобных существ или устройств. При строгом исследовании мы действительно найдем, что демоны Максвелла не могут существовать в равновесной системе, но если мы примем с самого начала эту невозможность и не будем пытаться доказать ее, то упустим прекрасный случай узнать кое-что об энтропии и о возможных физических, химических и биологических системах.

Чтобы демон Максвелла мог действовать, он должен получать от приближающихся частиц информацию об их скорости и точке удара о стенку. Независимо от того, связаны ли эти импульсы с переносом энергии или нет, они предполагают связь между демоном и газом. Но закон возрастания энтропии справедлив для полностью изолированной системы и неприменим к неизолированной части такой системы. Поэтому мы должны рассматривать энтропию системы газ — демон, а не энтропию одного газа. Энтропия газа есть лишь компонент общей энтропии более широкой системы. Можно ли найти другие, связанные с демоном компоненты, входящие в общую энтропию?

Без малейшего сомнения, можно. Демон способен действовать лишь на основании принимаемой информации, а эта информация, как мы увидим в следующей главе, представляет собой отрицательную энтропию. Информация должна переноситься каким-то физическим процессом, например какой-то формой излучения. Можно вполне допустить, что эта информация переносится на очень низком энергетическом уровне и что перенос энергии от частицы к демону в течение продолжительного времени имеет гораздо меньшее значение, чем перенос информации. Но по законам квантовой механики [c.116] нельзя получить информацию о положении или импульсе частицы, а тем более о том и другом без воздействия на энергию исследуемой частицы, причем это воздействие должно превышать некоторый минимум, зависящий от частоты света, применяемого для исследования. Поэтому во всякой связи необходимо участвует энергия, и система, находящаяся в статистическом равновесии, должна находиться в равновесии как по отношению к энтропии, так и по отношению к энергии. В конечном счете максвеллов демон будет подвержен случайному движению, соответствующему температуре окружающей среды, и, как говорит Лейбниц о некоторых монадах, будет получать большое число малых впечатлений, пока не впадет в «головокружение» и не потеряет способность к ясным восприятиям. По существу, он перестанет действовать как максвеллов демон.

Тем не менее до того как демон собьется с толку, может пройти немалое время, и оно может оказаться столь продолжительным, что мы вправе называть активную фазу демона метастабильной. Нет оснований полагать, что метастабильные демоны в действительности не существуют; напротив, вполне возможно, что энзимы являются метастабильными максвелловыми демонами, которые уменьшают энтропию, пусть не разделением быстрых и медленных частиц, а каким-нибудь другим эквивалентным процессом. Мы вполне можем рассматривать живые организмы, как и самого Человека, в этом свете. Без сомнения, энзим и живой организм одинаково метастабильны: стабильное состояние энзима наступает, когда он перестает действовать, а стабильное состояние живого организма наступает с его смертью. Все катализаторы в конце концов отравляются, ибо они изменяют лишь скорости реакций, но не меняют истинного равновесия. Тем не менее и катализаторы, и человек имеют настолько определенные состояния метастабильности, что эти состояния можно считать относительно постоянными.

Я не хотел бы кончить эту главу, не сказав, что эргодическая теория — гораздо более обширный предмет, нежели здесь изложено. В некоторых новейших направлениях эргодической теории мера, остающаяся инвариантной при группе преобразований, определяется непосредственно самой группой, а не задается заранее. [c.117] В особенности я должен упомянуть работы Крылова и Боголюбова и некоторые работы Гуревича и японской школы.

Следующая глава посвящена статистической механике временных рядов. В этой области условия также очень далеки от условий, принимаемых статистической механикой для тепловых двигателей, и поэтому они весьма хорошо могут служить моделью того, что происходит в живых организмах. [c.118]

Оглавление книги