Книга: Фундаментальные алгоритмы и структуры данных в Delphi

Результаты выполнения тестов

Результаты выполнения тестов

В разделе сопровождающих эту книгу материалов, который расположен на Web-сайте издательства, можно найти тестовую программу, которая применяет все рассмотренные нами тесты к стандартному генератору случайных чисел Delphi и минимальному стандартному генератору случайных чисел. На рис. 6.1 приведены результаты проведения одного из тестов для генератора случайных чисел Delphi.

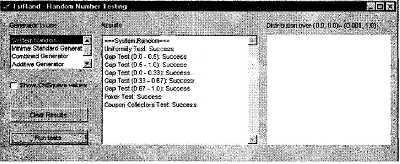
Рисунок. 6.1. Тестирование стандартного генератора Delphi

Как видите, данный конкретный тест свидетельствует о том, что стандартный генератор Delphi успешно прошел проверку. (под успешным прохождением теста понимается, что предложенная к тестированию последовательность случайных чисел не дает результатов, которые являются значимыми на уровне 5%.)

Окно в правой части окна программы представляет собой снимок случайных чисел, полученных на выходе генератора. Координаты точек вычисляются на основе двух случайных чисел: первого для оси х, а второго - для оси Y. После этого точки выводятся в окне, если они находятся в прямоугольнике (0.0, 0.0, 0.001, 1.0) или, другими словами, в прямоугольнике, нижний левый угол которого расположен в точке (0.0, 0.0), а верхний правый - в точке (0.001, 1.0). Чтобы распределение точек было удобнее изучать, прямоугольник растянут по оси х. Как видите, на рисунке точки случайным образом разбросаны по всему прямоугольнику. Никакой системы при этом не наблюдается.

У вас может возникнуть удивление, зачем мы так много говорим об этом окне. Посмотрите на рис. 6.2, на котором показана та же программа, но для минимального стандартного генератора случайных чисел. Как видите, и этот генератор успешно прошел все тесты, но посмотрите на распределение случайных точек. Очевидно, что генератор дает последовательность случайных чисел, которые при переносе их на график формируют определенный регулярный рисунок.

Регулярность минимального стандартного генератора не позволяет использовать его для некоторых приложений, особенно тех, которые требуют пар случайных чисел. Даже незначительной регулярности бывает достаточно для того, чтобы приложение давало неверные результаты. Кроме того, отсутствие регулярности в результатах стандартного генератора случайных чисел Delphi в двухмерной плоскости не означает, что регулярности не будет в гиперплоскостях более высокой размерности. Существуют тесты, которые проверяют случайные числа на наличие регулярности в А> мерном пространстве, но давайте не будем погружаться в изучение слишком сложных тестов, а рассмотрим методы использования двух уже известных нам генераторов для дальнейшей рандомизации их выходных данных.

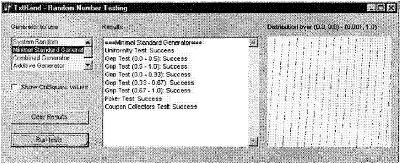
Рисунок 6.2. Тестирование минимального стандартного генератора

Мы рассмотрим три метода: первый известен как комбинаторный, второй - аддитивный и третий - метод тасования.

Оглавление книги