Книга: Windows XP
Двоичная система
Двоичная система
Вернемся к «азбуке» информационной науки. Впрочем, азбука ли это? Ведь букв-то как раз здесь и нет, одни цифры – не зря же компьютерные технологии называют еще и «цифровыми». Да и цифр немного – всего две:
? 0 – отсутствие сигнала;
? 1 – его наличие.
Хорошая азбука, что и говорить! Такую даже первоклассник выучит за секунду. Да только мала – много ли слов составишь из ее «букв»? Немного. Но для компьютера – вполне достаточно. И как же по научному называется такая система счисления из двух цифр? Нетрудно догадаться, что двоичной.
Двоичная система счисления действительно очень простая, даже самая простая. Для подтверждения этой мысли представим таблицы умножения и сложения двоичной системы.
Сначала – таблица умножения.Если вспоминается таблица умножения десятичной системы, забудьте как страшный сон. Мало есть вещей, более простых, чем таблица умножения двоичной системы.
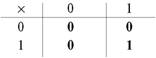
Какое в этой таблице самое сложное действие? Конечно, 1x1 = 1. Остальные ее действия – 0x0=0, 0x1=0, 1x0=0 – как говорят математики, абсолютно тривиальны.
Название таблицы сложения произошло, видимо, от слова «сложный». Таблица сложения двоичной системы не просто сложнее таблицы умножения. Она сложна по жизни. Точнее, камень преткновения составляет одно единственное действие, но на нем держится вся система и все компьютеры. Посмотрим на эту «страшную» таблицу сложения:
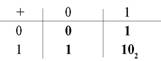
Вся суть этой таблицы – в ее самом сложном действии: 1 + 1 = 102 «один-ноль». Остальные действия не представляют для нас никакой угрозы: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1. А что это за индекс «два» у числа 102? Индекс два пришлось записать в этом числе, чтобы обозначить, что оно записано в двоичной системе счисления. Да, число 102 вовсе не равно десяти в «школьной» десятичной системе. Хотя и пишется как десять с индексом два. Здесь как раз тот самый случай: наш язык десятичный, и называть адекватно числа в других системах он не может.
Какое же количество обозначает это число 102? Давайте посчитаем. Оно получено сложением двух единиц, и поэтому обозначает количество два. Только записано оно в двоичной системе. А что прикажете делать? Ведь у двоичной системы в арсенале всего две цифры: 0 да 1. И как тогда обозначить число, следующее за 1? А как обозначается число в десятичной системе, которое следует сразу за самой большой цифрой 9? Вот точно так же и в двоичной системе. Только с двоечкой внизу.
Другими словами, 102 = 210: «один-ноль» в двоичной системе равно двум в десятичной. Ах, язык, язык… Обратите внимание: основание системы счисления справа внизу у чисел пишется всегда в десятичной системе!
Для тренировки выпишем первые двоичные числа от 0 до 16. Воспользуемся при этом основным свойством чисел: следующее число больше предыдущего на 1.
0 и 1 можно писать без указания системы счисления: 0 и 1 и в Африке 0 и 1.
Самый эффективный способ получить следующее число – это прибавить один столбиком. Да, да, тем самым «школьным» столбиком. Он прекрасно «работает» в любых системах счисления. Сначала получим:
1 + 1 = 102 (называется не «десять», а «один-ноль», то есть перечисляются названия цифр слева направо);
102 + 1 = 112 («один-один»);
112 + 1 = 1002 («один-ноль-ноль») и так далее.
Как нетрудно заметить, главное в этом деле – все время помнить, что один да один будет не два, а «один-ноль». Нуль пишем, один в уме…
Следует иметь в виду: заложенная в русский язык десятичная система ни в коем случае не должна использоваться для называния чисел в других системах.
Если продолжить это увлекательное занятие, то получится следующая таблица с первыми 16 двоичными (и десятичными) числами, не считая нуля.
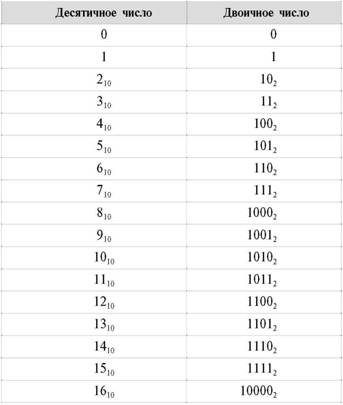
Теперь, имея такую чудную таблицу, займемся важным делом: подсчитаем, сколько же разных слов можно составить из наших цифровых «букв». То есть снова посчитаем количество чисел с одинаковым количеством цифр, но уже в двоичной системе счисления. Только не запутайтесь: подсчет будем вести в десятичной системе.
Итак, изучая эту таблицу, получаем:
? 2 однозначных двоичных числа 0 и 1;
? 4 = 22 двузначных двоичных числа: 00, 01, 102 и 112;
? 8 = 23 трехзначных двоичных чисел от 000 до 1112;
? 16 = 24 четырехзначных двоичных чисел от 0000 до 11112.
Уф! Дело сделано. Позволим себе рассуждать по аналогии и, учитывая подобный опыт подсчета количества таких чисел для десятичной системы, получим уникальную таблицу количества всех двоичных чисел, имеющих один знак, два знака, три знака и так далее до десяти знаков.
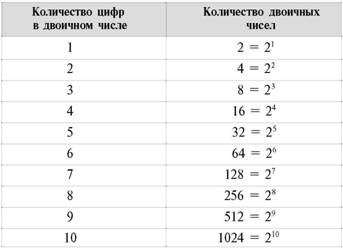
- Шестнадцатеричная система
- Система безопасности InterBase
- Что делать, если при установке принтера появляется сообщение Невозможно завершение операции. Подсистема печати недоступн...
- 7 Система Цикл: долгосрочные цели
- 3. Система конкурентных продаж (продажи по методу КЛИН)
- 3.4 Сетевая файловая система
- 3.7 Система Microsoft Exchange 2000 и NAS
- 6.5 Файловая система NTFS
- 1.3.1. Индексирование сайта в поисковых системах
- 6.6.2.1. Файловая система FAT 16
- 6.6.2. Файловая система FAT
- 4 Файловая система Linux




