Книга: Windows XP

Десятичная система

Обычных «школьных» цифр всего десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью можно записать любые числа (количества), но для этого нужно использовать определенные правила, которые всем известны со школы. Так вот, цифры вместе с правилами записи чисел и называются системой счисления.

Вспомним, как записываются эти числа. При записи числа каждая цифра, которая входит в его запись, означает определенное количество. Какое? Давайте посмотрим пример. Возьмем число 4891. Как оно получается из своих цифр? А вот как:

4891 = 4x1000 + 8x100 + 9x10 + 1x1.

Мы видим, что количество, которое несет в себе каждая цифра, зависит от положения, позиции цифры в записи числа. Если цифра стоит на первом месте справа, то ее следует домножить на 1, если на втором месте справа – то на 10, на третьем – на 100 и так далее, пока число не кончится. По этой причине такая система счисления называется позиционной. Вспоминая, что количество цифр «школьной» системы равно десяти, получаем ее полное название – позиционная десятичная система счисления.Количество цифр позиционной системы счисления называется ее основанием. То есть «школьная» система счисления имеет своим основанием десять.

Сделаем еще одно существенное замечание: наш русский язык представляет собой десятичный язык. Все числа, которые мы произносим, составлены по правилам десятичной системы счисления. (Поскольку все системы счисления, с которыми мы будем знакомиться, суть позиционные, слово «позиционная» будем опускать.) С одной стороны, это удобно и привычно, мы даже этого не замечаем. Но, с другой стороны, у нас будут возникать трудности при именовании чисел, записанных в других, недесятичных системах, – просто не будет слов.

Очень важно и то, что цифры умножаются только на степени числа 10. Поэтому наше число можно записать еще и так:

4891 = 4х10^3 + 8х10^2 + 9x10^1 + 1x10^°.

Следует также заметить, что приписывание любой цифры справа от числа меняет число. Например, числа 4, 48, 489, 4891, 48910 – все разные. Приписывание цифры слева также меняет число, но только в случае, если эта цифра – не нуль. Так, числа 0, 10, 910, 8910, 48910 – также все разные. А вот числа 48, 048, 0048, 00048 являются одним и тем же числом – 48. Таким образом, приписывание слева нуля не меняет числа – не меняет количества, которое обозначает число.

Наконец, при знакомстве с другими системами – нам пригодится такое понятие, как количество цифр в числе. Количество цифр в числе – это количество цифр в числе. Однако дело здесь не так просто, как может показаться на первый взгляд. Для начала перечислим все однозначные десятичные числа:

О, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Да, это просто цифры. Но это не означает, что цифра и однозначное число – одно и то же. Цифра – это цифра, то есть знак. А число, пусть даже и однозначное – это количество. Итак, однозначных чисел ровно десять.

Перейдем к двузначным. Какое самое большое двузначное число? Правильно, 99. А самое маленькое? 10? Вот и не угадали. 01? Снова не угадали. На компьютере самое маленькое двузначное число – это 00. И только следом по порядку идет двузначное число 01. Потом – 02 и так далее. Список всех двузначных чисел выглядит так:

00, 01, 02, 03, …, 97, 98, 99.

Сколько всего? Правильно, ровно сто. Теперь легко можно догадаться, сколько всего существует трехзначных, четырехзначных и так далее десятичных чисел. Сведем наши знания в следующую таблицу.

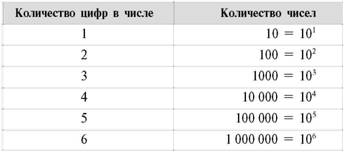
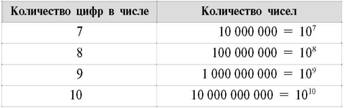
Что означает эта таблица? А означает она то, что однозначными числами можно закодировать 10 объектов, двузначными – 100 объектов и так далее. Например, количество автомобильных номеров с одинаковыми буквами и разными цифрами ровно 1000 – ведь автомобильный номер содержит три цифры. Разных телефонных номеров в Москве может быть ровно десять миллионов: каждый телефонный номер состоит из семи цифр (без учета цифр кода города).

Оглавление книги