Книга: Вычислительное мышление: Метод решения сложных задач

Жизнь как игра

Жизнь как игра

Давайте начнем с простого — с игры, в которой есть квадратная сетка и набор правил, в зависимости от которых на ней появляются и исчезают пикселы. Значение пиксела меняется и зависит от того, сколько других пикселов находится рядом. Звучит не очень интересно, правда? Но не торопитесь с выводами. Даже в этой простой игре происходит много интересного, и мы используем ее, чтобы кое-что понять о мире природы.

Игра называется , ее автор — математик . Впервые правила игры были опубликованы в 1970 г., и впоследствии она приобрела популярность у программистов по всему миру. Правила просты, хотя Конвей приложил массу усилий, чтобы их правильно сбалансировать и гарантировать интересный игровой процесс.

Сетка представляет собой небольшой квадратный мир с (пикселами), которые могут присутствовать (быть живыми) и отсутствовать (быть мертвыми). У каждой клетки есть окружение из восьми других, которые непосредственно прилегают к ней по горизонтали, вертикали и диагонали. Чтобы выжить, существующая живая клетка должна иметь два или три живых соседа — этого достаточно для поддержания жизни, но не слишком много. Если у любой живой клетки окажется менее двух соседних, она умрет из-за недостаточной населенности. Подобным образом любая живая клетка, у которой более трех живых соседей, умрет от перенаселения. Наконец, каждая живая клетка, у которой есть три живых соседа, активизируется и имитирует процесс размножения. Эти принципы обобщены в на рис. 55.

На рис. 56 показан пример такой модели и один жизненный цикл.

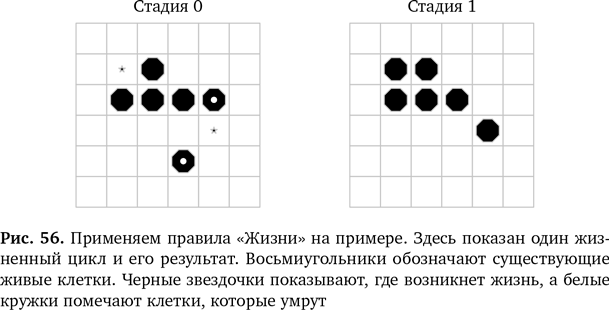
Благодаря этой простой математике и простому набору порождающих правил, которые применяются к клеткам на сетке, на игровом поле возникают странные и интересные модели, которые с течением времени меняются. Клетки живут и умирают по заданным правилам.

Вы можете сыграть в эту игру самостоятельно. Для этого понадобится большая сетка. Для начала сгодится шахматная доска, но вы скоро осознаете, что нужно больше пространства. Больше подойдет доска для игры в го, если она у вас найдется. Как вариант, можно нарисовать большую сетку на самом большом листе бумаги, какой вы только найдете. В идеале лист должен быть бесконечным, но тогда он не поместится в вашу спальню… поэтому придется принять, что, если игра дойдет до края доски, нужно будет быстро найти еще место либо признать, что это конец «Жизни» и все ваши существа упадут с края «вселенной».

Необходимо как-то помечать рождающиеся клетки. Полезно также выделять те, которые в следующем раунде умрут. Убирать их нельзя — они нужны, чтобы просчитать все изменения. К примеру, можно взять камни для игры в го — замените черные на белые, чтобы показать, какие клетки скоро умрут (и отправятся на небо). Еще вам понадобится как-то помечать квадраты, в которых зародится жизнь. Для этого используйте более мелкие предметы (например, бусины) другого цвета. Можно использовать три вида монет или цветных бусин (но, если в вашем мире закипит жизнь, их понадобится очень много).

Теперь остается только произвольно разместить фишки на доске, а потом рабски следовать законам «Жизни». В вашем мире это эквиваленты физических законов. Сначала определите все рождения и смерти, заменив фишки на новые на всей доске, а потом уберите умирающие клетки и замените живые на новорожденные, чтобы подготовиться к следующему раунду. Чтобы играть в «Жизнь», нужно уделять много внимания деталям. Если вы сделаете ошибку с одной клеткой, у вас получится совершенно другой расклад.

В интернете вы найдете самые разные симуляции и с их помощью увидите, как развивается жизнь в более крупных масштабах. Конечно, если вы умеете программировать, то попробуйте создать собственный вариант. В систему Turtle («Черепаха»), разработанную в Оксфордском университете (www.turtle.ox.ac.uk), входит программа игры «Жизнь», которая может послужить образцом.

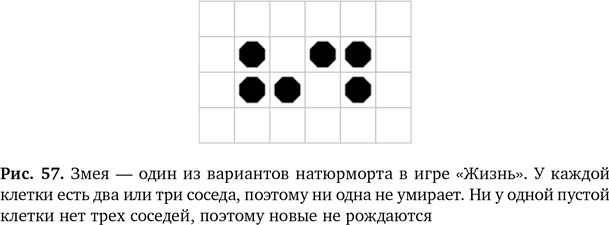
Конвей обнаружил, что некоторые комбинации являются статичными. Они остаются в одном и том же месте игрового поля без изменений, поэтому он назвал их — как, например, змею на рис. 57. Какие еще простые начальные комбинации, относящиеся к натюрмортам, вам удастся найти?

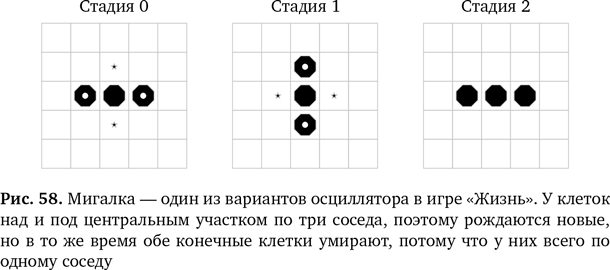
Некоторые шаблоны меняют форму, проходя через фиксированный набор вторичных шаблонов, в конце концов возвращаются к исходному варианту — и снова начинают бесконечный повторяющийся цикл. Их назвали Например, очень простой осциллятор, так называемая , показан на рис. 58. Если начать с набора мигалок, которые находятся на достаточном расстоянии, чтобы не мешать друг другу, вы создадите замечательные мерцающие узоры. Такие комбинации из группы осцилляторов называются по имени необычных звезд, на которых с определенной периодичностью происходят всплески энергии.

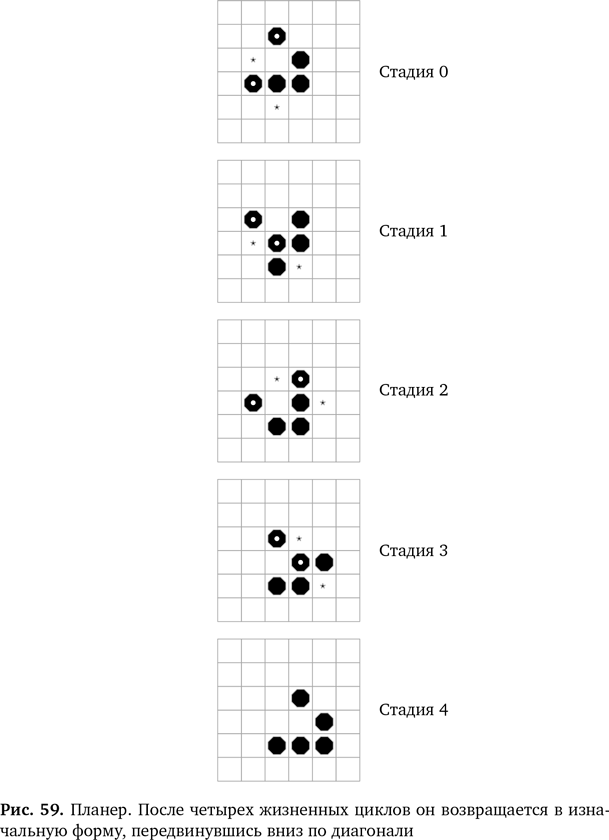
Коллега Конвея натолкнулся на удивительные фигуры, которые сохраняют форму, но передвигаются по сетке. Их назвали (рис. 59). В целом движущиеся конфигурации называют

В игре «Жизнь» даже можно имитировать логические вентили. Как мы говорили выше, это базовые составляющие компьютера. Их делают из транзисторов, нейронов и… из клеток игры «Жизнь». Это значит, что, располагая достаточно большой сеткой, можно создать на ней работающий компьютер — исключительно из клеток, следующих этим простым правилам.

Информатики начали предлагать новые разновидности игры — трехмерные решетки, шестиугольную решетку и так далее. Изменив игровое пространство и правила, они обнаружили, что по мере того, как компьютер повторяет нужные действия и вносит изменения, на решетке появляются еще более интересные конфигурации.

Со временем изобретение Конвея стали называть и сочли новым способом проводить вычисления. Правила можно адаптировать так, чтобы клетки проводили вычисления разного рода. Простые клетки с простыми правилами можно заменить и даже усложнить. Каждая клетка в этом случае становится который находится в определенной позиции на решетке и содержит код с собственным набором правил. Когда автомат входит в контакт с информацией, размещенной на решетке, он «переваривает» сначала свои данные, а затем данные из ближайших окрестностей, и на выходе дает результат. Результат зависит от нескольких предыдущих (скажем, 10) состояний клетки. Изначальными правилами Конвея при этом полностью пренебрегают.

Такого рода сложные клеточные автоматы находят самое разное применения. Их, например, настраивают на изучение природы — чтобы они исследовали, как в тропических лесах распространяются растения, как развиваются коралловые рифы, как проявляется сейсмическая активность, как мигрируют животные. Каждая клетка при этом становится небольшого участка мира. В ней закодированы правила поведения и взаимодействия с другими клетками, свойственные интересующему ученых объекту. Клеточные автоматы обеспечили новый способ изучения экологии с помощью на основе клеток.

Клеточный автомат помогает понять, как на дорогах образуются пробки и как в популяции распространяется болезнь. В криптографии данные, которые нужно зашифровать, размещают в сетке и исследуют с помощью автомата. Благодаря простым правилам каждый в состоянии зашифровать сообщение. Но расшифровать его, не зная ключа, нелегко. Клеточные автоматы даже использовали для сочинения музыки — и для многих других задач. Неплохой результат для того, что началось с несложной игры на простой доске.

Оглавление книги