Книга: Вычислительное мышление: Метод решения сложных задач

Две задачи

Две задачи

В головоломке «Ход конем» один шахматный конь может передвигаться по небольшой доске в форме креста. Конь ходит на два поля в любом направлении, а потом на одно поле перпендикулярно этому направлению или наоборот. Он переходит на новое поле, не останавливаясь на полях между начальным и конечным, и всегда должен оставаться в пределах доски. Возможные первые ходы в головоломке показаны на рис. 32.

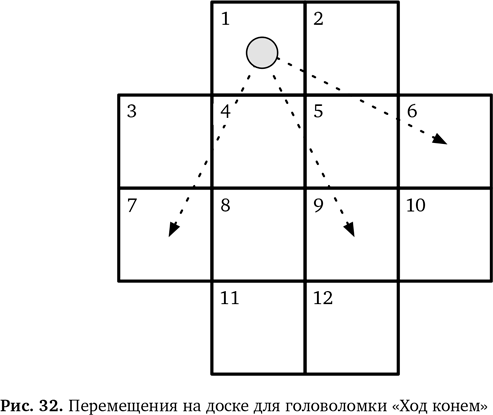
Вам нужно найти последовательность ходов, начиная с поля 1, чтобы конь побывал на всех полях ровно один раз и вернулся в исходную точку.

Попробуйте решить задачу «Ход конем», замерив, сколько времени у вас уйдет. При этом недостаточно, чтобы конь прошел заданный путь. Необходимо найти алгоритмическое решение, а не просто двигать фигуру по доске. Для этого нужно записать серию перемещений, которые приведут к ответу. То есть придется применить алгоритмическое мышление и вывести алгоритм для решения головоломки. Этот алгоритм можно записать в виде списка номеров, присвоенных полям, на которые ходит конь, в порядке прохождения. Или же записать алгоритм как серию команд вроде «перейти с поля 1 на поле 9». Решать вам.

Как только у вас появится работающий алгоритм, оцените его: проверьте, действительно ли работает это решение, опробовав его на практике. Следуйте собственным инструкциям, отмечая клетки по мере того, как их обходит конь. Таким образом вы сможете гарантировать, что он не нарушает правила и посещает каждую клетку ровно один раз. Если головоломка решена, прекрасно! Если нет, не беспокойтесь — ниже мы посмотрим, как облегчить эту задачу. Но сначала давайте попробуем решить задачу полегче.

Вы экскурсовод и работаете в отеле. Туристы из вашего отеля хотят отправиться на дневную экскурсию и посетить все достопримечательности города. Вам дали карту (рис. 33), на которой показано расположение достопримечательностей и указано, как добраться до них на метро.

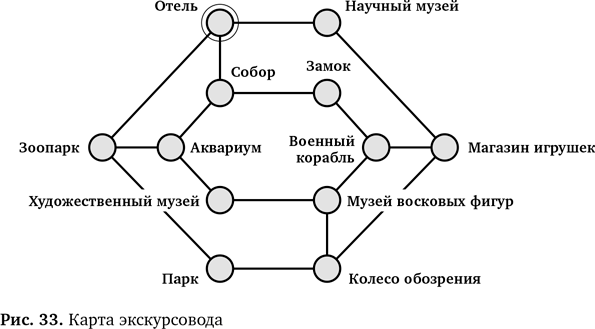
Вам нужно составить маршрут, который начнется в отеле и позволит показать вашей группе все интересные места. Туристы прибыли в город всего на день и не хотят терять времени. Очевидно, они будут недовольны, если придется два раза проходить через одно и то же место. Также очевидно, что вечером они хотят оказаться в отеле.

Как и в случае с «Ходом конем», задача — найти алгоритмическое решение. Убедитесь, что ваше решение действительно работает. Сколько времени у вас ушло? Оказалась ли эта задача легче, чем предыдущая (то есть вы решили ее быстрее)?

Почему важно проверить, верно ли ваше решение? Ну конечно, вам не хотелось бы отправиться на экскурсию и в конце дня обнаружить, что вы пропустили важную достопримечательность. Кому хочется разбираться с недовольными туристами!

Чтобы проверить алгоритм, нужно провести процедуру, которую в информатике называют . Это всего лишь означает, что сначала вы проходите все этапы алгоритма на бумаге. Вероятно, вы так и сделали, проверяя решения для «Хода конем». Для задачи, решаемой экскурсоводом, можно нарисовать маршрут на карте и, следуя инструкциям, помечать каждое посещенное место.

Конечно же, настоящий экскурсовод не удовлетворяется проверкой маршрута на бумаге. Он пойдет и проверит все в реальных условиях. Вы бы тоже пошли и проверили все сами, но, если сначала выполнить проверку на бумаге, это сэкономит массу времени. Программисты поступают точно так же. Сначала они проверяют, как программа работает на бумаге (трассировка), а потом испытывают ее в реальных условиях — проводят Так же, как в случае с вашей задачей, программисты делают это, чтобы гарантировать бесперебойную работу программ.

Вообще, процедуру можно сделать точнее. Для этого надо определить, какие именно особенности выполнения задачи важны, чтобы получить правильное решение. Если мы запишем список этих необходимых вещей, то сможем проверить, соответствует ли им найденное решение. В информатике такие особенности называются

Для задачи экскурсовода нужно проверить, удовлетворяет ли итог следующим требованиям.

Вернитесь назад и запишите список требований к головоломке «Ход конем». Видите что-нибудь похожее? Мы вернемся к этому ниже.

Возможно, вам показалось, что задача «Ход конем» сложнее, но на деле это не обязательно так. Решить ее будет очень легко, если использовать еще некоторые приемы из компьютерного мышления.

Почему задача экскурсовода легкая? Карта метро дает важную информацию, незначительные детали опущены. Это хороший пример — решение легко увидеть. Без карты было бы сложнее, даже если бы мы знали, где что находится. Карта метро — особый способ предоставления информации. Это особый вид схемы под названием В информатике под графом подразумевают несколько кружков (мы называем их графа) и линий, которые их объединяют ( графа). Вершины и ребра представляют те аспекты данных, которые нас интересуют. Ребра показывают, какие вершины объединены таким образом, что это важно для решения нашей задачи. Туристические достопримечательности, вероятно, соединены автомобильными дорогами, но по-другому. В этом случае граф пути был бы другим — и он понадобился бы нам, если бы мы организовывали автобусный тур!

Нас интересует, какие у нас есть достопримечательности (наши вершины) и какие из них соединены друг с другом линиями метро (наши ребра). Другие особенности этих мест нас не интересуют, поэтому мы их игнорируем. Мы опускаем их точное расположение, расстояние друг от друга, соединения автодорог и многие другие вещи, которые не относятся к нашей задаче — понять, как объехать все это на метро. Граф — это реального города. Мы спрятали все лишние детали, не нужные для построения графа. Здесь отражена только важная информация. Поэтому нам легко увидеть действительно необходимое для решения. Это хорошее текущей задачи.

Графы часто используются, чтобы представить информацию о связях между объектами. Это маршруты на автобусных остановках, карты поездов и метро. Граф — очень хорошее в ситуации, когда нужно проложить маршрут из одного места в другое, как в нашем случае. Упрощенный граф облегчает составление маршрута по сравнению с максимально точной картой, где трудно выделить нужную информацию среди многочисленных подробностей.

В информатике есть особое название для обхода графа, когда вы посещаете каждую вершину ровно один раз и возвращаетесь в начало. Это называется — по имени ирландского физика Уильяма Роуэна Гамильтона. Он изобрел головоломку, по условиям которой нужно было обойти все углы додекаэдра, проходя по его граням.

Оглавление книги