Книга: Вычислительное мышление: Метод решения сложных задач

Одно решение на двоих

Одно решение на двоих

Возможно, вы уже заметили, что головоломка «Ход конем» и задача экскурсовода очень похожи друг на друга. Если вы записали требования для «Хода конем», то, вероятно, увидели полное совпадение.

В обоих задачах вас просят найти гамильтонов цикл! Таким образом, мы использовали прием из вычислительного мышления. Мы обе задачи, чтобы они стали одинаковыми, и сделали это с помощью увидев важнейшие сходные черты. При этом мы от деталей, таких как отели и туристические достопримечательности или необходимость ходить конем или ехать по линиям метро.

Итак, задача экскурсовода оказалась легкой, потому что мы представили ее в виде графа. Так почему бы нам не сделать то же самое и с задачей «Ход конем»?

Для этого нужно в большей степени. Чтобы это сделать, необходимо осознать две вещи. Во-первых, не важно, как выглядит доска. Не важно, что поля — это квадраты. Их форма и размер могли бы быть абсолютно любыми. Давайте нарисуем каждое поле в виде кружочка — так же, как достопримечательности изображены на карте метро. Это просто вершины графа.

Во-вторых, какие поля на самом деле находятся рядом друг с другом — тоже не очень важно. Единственное, что имеет значение, — между какими полями конь перемещается. Поэтому давайте соединим линиями любые два кружка, между которыми можно сделать ход. Подобным образом карта метро показывает, между какими достопримечательностями можно переместиться на метро. Это ребра графа.

Чтобы сделать граф для головоломки «Ход конем», переходите с поля на поле и по мере продвижения рисуйте кружки и линии (вершины и ребра). Если четко выстроить путь, вы ничего не пропустите. Начните с поля 1. Нарисуйте кружок и пометьте его цифрой «1». Теперь с поля 1 можно перейти на поле 9 — значит нужно нарисовать еще один кружок, обозначить его как «9» и соединить их линиями. С поля 9 перейдите на поле 3 и нарисуйте еще один кружок, который пометьте «3» и соедините его линией с кружком 9.

Продолжайте так делать, пока не вернетесь к уже нарисованному кружку. Теперь отойдите на ход назад и попробуйте из этой точки пойти другой дорогой. Если других вариантов, которые вы еще не обозначили, больше нет, вернитесь еще на один ход и попробуйте оттуда. Продолжайте делать так до тех пор, пока не проведете эту операцию (она называется ) до поля 1 и у вас не кончатся варианты. В итоге вы получите схему.

Заметим, что из трех внутренних кружков возможны только два хода, а значит, на завершенной схеме на каждую из этих вершин придется по два ребра (линии). С других полей можно сделать три разных хода, поэтому у их вершин будет по три ребра.

Способ исследования всех возможных ходов с целью нарисовать граф называется мы исследуем пути до самого конца, например продвигаясь через 1 — 9 — 3 — 11... до конца, потом сохраняем этот путь и пробуем другие. Альтернативный вариант (под названием ) подразумевает рисование всех ребер, исходящих из вершины, и всех вершин, к которым они ведут, перед перемещением к новой вершине. Используя этот метод, мы могли бы нарисовать все ребра из вершины 9, потом все ребра из вершины 6 — и так далее. Это два разных алгоритма для исчерпывающего исследования графа — два разных Как только вы осознаете, что задачу можно в виде графа, то используйте любой из этих алгоритмов в качестве упорядоченного способа исследования графа и, соответственно, задачи.

Если ваш рисунок получился немного беспорядочным из-за наезжающих друг на друга линий, как показано на рис. 34, можно перерисовать его начисто, чтобы линии не пересекались. В этом случае используйте два связанных шестиугольника — один внутри другого, как на рис. 35.

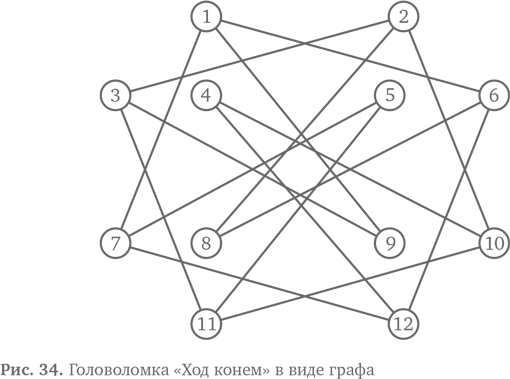
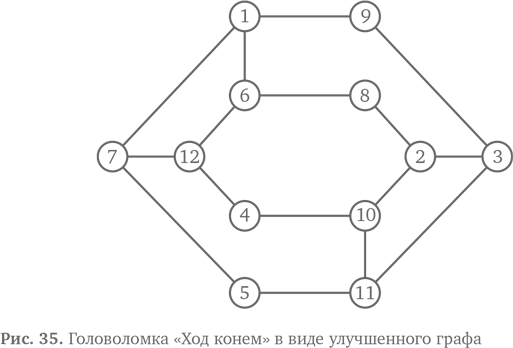
Когда вы аккуратно начертите граф, попробуйте снова решить задачу «Ход конем». Начните с вершины 1 и следуйте линиям, отмечая вершины, которые проходите. Теперь найти решение должно быть довольно легко.

Теперь внимательно посмотрите на чистый вариант графа. Мы перечертили его, не меняя ребер и вершин, и он выглядит в точности как схема метро. Единственная разница — в обозначениях вершин. Цифры вместо названий.

Теперь видно, что эти задачи можно и что они не просто похожи, но в точности одинаковы. Если у вас есть решение для одной задачи (алгоритм, позволяющий найти ответ), значит, есть и для другой! Все, что нужно сделать, — поменять обозначения. версия алгоритма подойдет для обеих головоломок, и ничего не придется делать заново.

На рис. 36 показано, как поменять обозначения на графе одной из наших задач, чтобы он подошел для другой. Еще на нем видно, как перевести решение одной задачи в решение другой. Обозначение каждого шага в алгоритме для одной из задач нужно заменить на соответствующее в другой.

Итак, если мы нашли следующее решение для задачи экскурсовода:

1. Отель.

2. Научный музей.

3. Магазин игрушек

4. Колесо обозрения.

5. Парк.

6. Зоопарк.

7. Аквариум.

8. Художественный музей.

9. Музей восковых фигур.

10. Военный корабль.

11. Замок.

12. Собор.

13. Отель,

то, используя таблицу, сразу же найдем решение для «Хода конем»:

1. Поле 1.

2. Поле 9.

3. Поле 3.

4. Поле 11.

5. Поле 5.

6. Поле 7.

7. Поле 12.

8. Поле 4.

9. Поле 10.

10. Поле 2.

11. Поле 8.

12. Поле 6.

13. Поле 1.

Эта таблица — еще один вид информации или в виде С ее помощью вы легко найдете эквивалент поля из «Хода конем» в списке достопримечательностей из задачи для экскурсовода. Но стоит заметить, что искать поле, соответствующее достопримечательности, не очень удобно. Было бы гораздо лучше, если бы достопримечательности стояли в алфавитном порядке.

Схема на рис. 37 — еще одно представление той же информации, полученное методом наложения. Также она показывает единое решение (для обеих задач). Конечно, поскольку решений может быть много, вы можете прийти к какому-то другому, но и тогда оно подойдет для обеих задач.

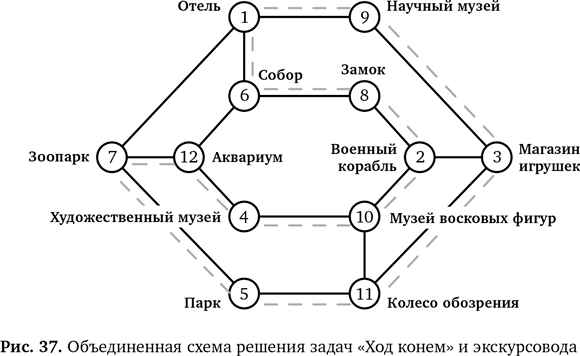
Итак — вероятно, это удивит вас, — две разные вроде бы задачи оказались одинаковыми и с одним решением (после ). Решив одну, вы сразу решили и другую! Это открытие происходит после выбора подходящих и подходящего двух задач ( в виде графа).

Оглавление книги