Книга: Криптография и свобода

Глава 8. Криптография

Глава 8. Криптография

Слово «криптография» впервые было произнесено перед нами только на 2 курсе. До этого – ни-ни, никаких упоминаний о будущей специальности. Полная секретность, все в точности так, как завещал товарищ Сталин: никому ни слова, ни жена, ни мать, ни отец – никто не должен знать о том, чем ты занимаешься. И вот на 2 курсе – посвящение в специальность, раскрытие (точнее, некоторое приоткрытие) тайны твоей будущей профессии.

После начались спецдисциплины, т.е. предметы, имеющие непосредственное отношение к криптографии. Первой была СД–7А – основы криптографии, там мы впервые познакомились с шифром простой замены и с методами его вскрытия, напоминающими разгадывание кроссвордов. Тоже предполагаешь некоторое вероятное слово, но подсказками и критериями истинности служат частота встречаемости знаков в шифртексте, расположение одинаковых знаков, пар, триграмм шифртекста. Первое практическое задание: надо вскрыть шифр простой замены по сравнительно небольшому тексту длиной около 100 знаков. Интересно было начало шифровки, в которой каждой паре цифр соответствовала одна буква русского алфавита: 45 32 18 45 32 18… Это означает, что в начале открытого текста первые три буквы повторяются, а такое начало не так уж часто бывает в обычной речи. Какие могут быть варианты?

– Две двери.

– Про проценты.

– При применении.

и, наверное, читатель сможет сам придумать еще несколько вариантов, но не очень много.

По смыслу в нашем учебном задании в качестве открытого текста должна быть какая-то фраза, которая связана с шифрами и основами криптографии. Вряд ли из приведенных выше трех вариантов первые две фразы имеют отношение к криптографии, поэтому наиболее вероятен третий вариант. Он и оказался истинным:

При применении шифров простой замены статистика знаков открытого текста совпадает со статистикой знаков шифртекста.

Это как в рассказе про пляшущих человечков у Конан Дойля: не важно, как переобозначить некоторую букву алфавита – другой буквой, цифрами или каким-то иным символом, вроде человечка с флажками. Повторяемость буквы в тексте приведет к повторяемости того символа, которым обозначена эта буква. Считайте статистику шифртекста, сопоставляйте наиболее часто повторяющимся символам наиболее часто повторяющиеся буквы алфавита (в русском языке – СЕНОВАЛИТР), подбирайте вероятные слова, по ним расставляйте остальные буквы и проверяйте читаемость открытого текста – все, простая замена вскрывается быстро и элементарно. И никакой особой математики для этого не нужно, скорее сообразительность, логика, знание лингвистических особенностей языка.

Но простая замена в криптографии – примерно то же самое, что ламповые диоды в электронике, дело далекого прошлого, представляет интерес только для истории. В современных шифрах используют гаммирование, т.е. сложение букв или знаков открытого текста с гаммой наложения. И вот тут знание некоторого вероятного слова в открытом тексте приводит к тому, что становится известным кусок гаммы наложения, а это уже пища для криптоаналитика.

С каким юмором нам рассказывали на СД–7А про шифрованные телеграммы, отправляемые в некоторые ближневосточные страны. Почти каждая из них начиналась с перечисления многочисленных и всем известных регалий адресата, по которым вычислялось такое количество гаммы, которое иногда позволяло вскрывать шифр и читать телеграмму быстрее, чем она доходила до адресата. Конечно же, это свидетельствовало также о слабости их шифров, нормальный стойкий шифр должен обеспечивать безопасность даже в таких случаях, но в криптографии есть правила хорошего тона, одно из которых справедливо гласит: не предавай огласке сведения из шифртелеграмм, не давай возможности противнику вычислить кусок гаммы наложения, это облегчает ему задачу вскрытия долговременных ключей шифрсистемы.

– Вот шифртелеграмма, которую я получил накануне!

Это уже 1989 год, съезд народных депутатов. Генерал, стоя на трибуне, показывает прямо в телекамеру содержание шифртелеграммы, тот самый открытый текст, по которому легко вычисляется гамма наложения. И не в какой-нибудь ближневосточной стране, а в СССР. Мораль отсюда следует простая: советский военный шифр должен быть еще и стойким к проявлениям военного идиотизма.

На лекциях по основам криптографии нас последовательно подводили к мысли, что только строгий математический подход, основанный на результатах Шеннона, способен обеспечить гарантированную стойкость шифра. Всякие простые или чуть усложненные замены, коды, не обеспечивающие равновероятности шифртекста, перестановки знаков открытого текста без последующей перешифровки – это все ненадежно, нестойко, рассчитано на слабого противника. Хочешь быть спокойным за свои шифры – используй в них только то, что дает надежную гарантию стойкости при любом уровне подготовки криптоаналитиков-оппонентов. А уровень подготовки криптографов в США, по определению, не ниже, а даже может быть и выше, чем в СССР. Американцы давно следят за нашими линиями связи, знают общий характер переписки, умеют выделять служебные символы, используют протяжку вероятного слова, знают статистику языка и может быть еще многое другое. Хочешь иметь стойкий шифр — доверяй только строгим математическим оценкам!

Дисковые шифраторы – вот, пожалуй, первая попытка построить удобные шифры гарантированной стойкости. Для них можно выписать уравнения шифрования и более-менее точно подсчитать количество различных вариантов параметров, которые нужно будет опробовать для вскрытия ключа к такому шифру.

Дисковые шифраторы были изобретены очень давно, еще до второй мировой войны. Они предназначены для шифрования телеграфных сообщений, состоящих из обычных букв латинского алфавита. Идея их построения очень простая. Каждой из 26 латинских букв ставится в соответствие один контакт на входе. При нажатии на клавишу, соответствующую этой букве, на данный контакт поступает электрический импульс, который начинает свое движение по цепочке дисков. Каждый диск представляет из себя колесо, на котором есть входные и выходные контакты, связанные между собой проводами-перепайками так, что одному контакту на входе соответствует строго один контакт на выходе. В математике такую конструкцию принято еще называть подстановкой. В результате после прохождения всей цепочки дисков на выходе появляется электрический импульс только на одном контакте. Буква, соответствующая этому контакту, является буквой шифртекста.

Диски в процессе шифрования вращаются друг относительно друга и тем самым обеспечивается отсутствие простой замены: одна и та же буква, зашифрованная в разные моменты времени, с большой вероятностью даст различные буквы в шифртексте.

Историю возникновения дисковых шифраторов, а также их подробное описание и характеристики нам рассказывали на СД–7Б. Сейчас все это можно прочитать в упоминавшейся уже ранее книге Дэвида Кана «Взломщики кодов». Здесь же мне хотелось бы упомянуть об одном весьма интересном эпизоде из лекций по СД–7Б, который я потом неоднократно вспоминал в своей дальнейшей работе.

У дискового шифратора есть два типа ключей. Одни ключи – долговременные, это перепайки между контактами дисков, т.е. те подстановки, которые соответствуют каждому диску. Их смена означает смену самого диска, и производится довольно редко, например, раз в месяц или даже в год. Другие ключи – начальное расположение дисков друг относительно друга. Их можно менять гораздо чаще, делать различными для каждой телеграммы в зависимости от ее номера. Такие ключи называются сеансовыми или разовыми. Количество долговременных ключей – всевозможных подстановок — огромно. Для каждого диска может быть всего 26! (26 факториал – произведение всех чисел от 1 до 26) различных вариантов его перепаек, а дисков несколько, иногда по 6, поэтому общее количество долговременных ключей получается совершенно фантастическим, (26!)⁶, нечего даже и думать о возможности опробования такого числа вариантов. Разовых же ключей намного меньше, всего (26)⁶ различных вариантов, даже во времена «Руты–110» было ясно, что такая работа по силам ЭВМ. Сюда еще добавляются разные заморочки, связанные с законом движения дисков друг относительно друга, но общий вывод можно сделать один: без знания подстановок надеяться дешифровать дисковый шифратор бесполезно. И вот тут лектор произнес одну замечательную фразу:

– Вы спросите, как вычисляются долговременные ключи? А никак, они покупаются.

Заходишь в магазин и покупаешь. На самом деле сейчас широко известно несколько детективных историй о том, как именно добывались долговременные ключи. Одна из таких историй – о немецкой подводной лодке U–571 времен второй мировой войны и находящемся на ней дисковом шифраторе «Энигма», захваченном американцами только для того, чтобы «купить» неизвестные подстановки.

Невозможность перебора долговременных ключей в дисковых шифраторах была равносильна признанию аксиомы в криптографии, аналогично той, что в геометрии прямая короче всякой другой линии, соединяющей ее концы, что в мат. анализе последовательность натуральных чисел бесконечна, что в физике справедливы законы Ньютона. Иметь дело с неизвестными факториальными ключами-подстановками, пытаться их определить, как-то вычислить – занятие малоприятное, в большинстве случаев просто бесполезное, их можно только «купить».

И вот тут начались вопросы и ответы.

– А почему нельзя сделать подстановку разовым ключом?

– Менять каждый раз диск в дисковом шифраторе долго, сложно и дорого.

– А не в дисковом? А, например, в шифре на новой элементной базе, работающем с байтами?

И уже много позже:

– А если мы реализуем шифр программно, то почему там нельзя использовать разовые факториальные ключи?

Можно, и еще как! Наличие факториальных ключей в криптосхеме, работающей с байтами по типу традиционного регистра сдвига, подрубает на корню все усилия криптоаналитика выписать и проанализировать уравнения шифрования, найти в них какие-то зависимости. Подстановка неизвестна – все, суши весла. Но если в дисковом шифраторе подстановки были долговременными ключами по объективным причинам, то в программном шифре все эти причины исчезли, запросто можно сделать факториальные ключи разовыми! Первый этап – схема работает вхолостую, выработанная генератором гамма идет на внутренние цели, выработку факториальных ключей-подстановок. А на втором этапе традиционный регистр сдвига, работающий с байтами и дополненный ключами-подстановками, начинает вырабатывать гамму наложения для шифрования открытого текста. За счет факториальных ключей схема может быть сильно упрощена и работать в дальнейшем с огромной скоростью, намного перекрывающей все небольшие издержки начальной холостой работы. Для такой схемы пусть хоть весь Генштаб каждый день трясет перед телекамерами CNN своими шифрованными телеграммами, дразнит ими АНБ вволю, до факториальных ключей им все равно не добраться!

Идея факториальных ключей вызревала давно. Оценки стойкости схем с факториальными ключами колебались от 10¹⁰⁰ до 10¹⁰⁰⁰, при желании можно сделать и больше, но это уже было бы изощрением. Скорости работы факториальных схем превосходили скорость программной реализации DES на порядок. К концу 80–х годов стало очевидно: факториальные схемы на новой элементной базе – это весьма перспективное направление развития шифров, сочетающее в себе высокую скорость и гарантированную стойкость. И что же дальше?

– Вы не выдвигали вашу схему на стандарт шифрования?

Да уж, чем-чем, а любовью к бумаготворческой деятельности Господь меня не наградил. Играть в бюрократические игры, состязаться в казуистике (а секретов врагам не выдадим?) – это не по мне.

– Нет.

Конкурент в лице заместителя начальника Спецуправления 8 Главного управления КГБ СССР вздохнул спокойнее. Действительно, доказывать кагалу начальников, что советским стандартом шифрования должна быть новая и перспективная схема, а не допотопная копия DES, что заветы Сталина уже устарели, что кибернетика – это не буржуазная лженаука, а сегодняшний и уж тем более завтрашний день криптографии, — это бесполезный Сизифов труд. По крайней мере, в СССР в то время.

Да, честно говоря, в конце 80–х годов пропихнуть какую-то оригинальную криптосхему в качестве открытого стандарта шифрования было абсолютно нереально. Слишком силен еще был синдром тотальной секретности в криптографии, вряд ли какой начальник решился бы взять на себя ответственность дать добро на опубликование каких-то оригинальных криптографических результатов. Переделайте немного DES, придайте ему совковый вид, но никаких своих секретов при этом не раскрывать! Это уже позже шелест зеленых купюр немного приоткрыл у Сталинской криптографической системы ту таинственность, за которой подчас скрывались элементарное ничегонеделание, нежелание начальников брать на себя даже самую малую долю ответственности, тихое стоячее болото. Но про это мы еще поговорим попозже, а пока вернемся в 70–е годы, на 4 факультет.

Что такое электронные шифраторы? Это то, что пришло на смену дисковым шифраторам. Постепенно идеи механических колес, рукояток, вращаемых человеком, штифтов, перепаек и перемычек стали анахронизмом. Появились полупроводники, транзисторы и первые логические элементы, с помощью которых стало возможным реализовывать криптографические преобразования, в которых алфавитом открытого и шифрованного текстов является множество, состоящее только из двух элементов – 0 и 1. Любую букву любого алфавита можно представить в виде двоичного вектора, следовательно, электронный шифратор пригоден для шифрования любой информации. Как шифровать? Конечно же гаммированием, наложением двоичной гаммы на двоичный текст. Задача простая: придумать генератор двоичной гаммы, зависящий от ключа, в котором вычисление такого ключа при некотором известном отрезке гаммы было бы таким трудоемким, что делало бы эту задачу неразрешимой за реальное время. Ну и, естественно, чтобы такой генератор был не очень сложно реализуем с помощью имеющихся типовых логических элементов.

Ключевое слово в электронных шифраторах – балалайка. Так вполне естественно обозвали типовой и самый распространенный узел в генераторах двоичной гаммы.

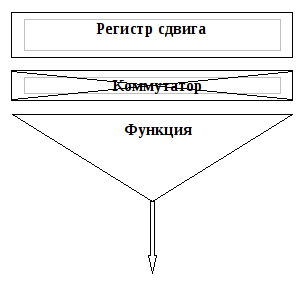
Из подобных балалаек, соединяя их различными способами друг с другом, и стали создавать различные генераторы двоичной гаммы, предназначенные для электронных шифраторов. Тут уже никакой лингвистики, никаких кроссвордов, как в шифрах простой замены. Нужно скрупулезно и точно просчитывать различные математические свойства этих балалаек: периодичность, статистику, группу преобразований, вероятности перекрытия гаммы и т.п.

Балалайки дали сильный толчок к развитию статистических методов анализа шифров. Если в дисковых шифраторах объем шифрованной переписки был сравнительно небольшой, то при использовании электронных шифраторов объем двоичной гаммы мог уже достигать нескольких миллионов знаков. А тогда, при каких-то огрехах в функции усложнения, появлялась возможность строить различные статистические аналоги, т.е. находить сразу целые классы ключей, реализующих статистически близкие гаммы.

В типовой балалайке присутствует коммутатор. Это, как правило, механический элемент, набор перемычек между контактами регистра сдвига и функции усложнения, т.е. факториальный ключ, подобный диску в дисковом шифраторе. Но опять же, как и в дисковых шифраторах, это долговременный ключ, разовыми ключами, как правило, являлись начальные заполнения регистра сдвига. Здесь, конечно же, коммутатор в какой-то степени «сглаживался» функцией усложнения, которая за один такт из двоичного вектора выдавала только один двоичный знак, но тем не менее задача определения коммутатора была весьма нетривиальной.

Электронным шифраторам была посвящена отдельная спецдисциплина – СД–7В. Нолики и единички, балалайки справа и слева — все это добро аппаратно реализовывалось и запихивалось в довольно большие ящики в 60–х годах. И, естественно, часто ломалось, а посему следующей спецдисциплиной, СД–7Г, был инженерно-криптографический анализ электронных шифраторов. Закоротило где-нибудь в ящике с шифратором, отвалился контактик, полетел транзистор – не опасно ли? Не полезет ли в линию связи открытый текст? Как заблокировать потенциально опасные неисправности? Как оценить вероятность отсутствия опасных неисправностей? В общем, все рутинные вопросы, очень важные, конечно, но скучные. Элементная база, электроника в первую очередь, должна быть понадежней, культура ее производства повыше.

Попыткой некоторого обобщения понятия шифратор, своего рода криптографической абстракцией, была теория шифрующих автоматов. В ней как бы намечались основные требования, которым должен удовлетворять современный шифратор: большая группа реализуемых преобразований, гарантированный период, стойкость к различным методам гомоморфизмов и т.п. Здесь, естественно, было полное царствование математики, а посему эта СД (кажется, СД–7Е) пользовалась большим уважением. Там нас впервые познакомили с таким свойством шифра, как имитостойкость, т.е. стойкость к попыткам целенаправленного искажения шифртекста и навязывания ложной информации. Историю возникновения самого понятия имитостойкости приводили следующую. В 60–е годы, во время войны во Вьетнаме, поставленные вьетнамцам советские ракеты класса «земля-воздух» управлялись с земли с помощью шифрованных команд. Американцы, имея мощные станции подавления таких радиосигналов, научились подавлять истинные команды управления ракетой и посылать вместо них ложные, заменяя некоторые знаки в перехваченных шифрованных сообщениях. В результате наши ракеты стали летать не в ту степь, а криптографы схватились за голову. Имитостойкость – это как бы отдаленная родственница электронной подписи, цели, которые преследует имитозащита шифра и система электронной подписи, весьма близки.

Ну и конечно теория информации, теория кодирования, коды исправляющие ошибки, энтропия, избыточность текста и все связанные с этим теоремы и задачи. Хотя большинство результатов по теории информации были в то время опубликованы в открытых изданиях (основополагающая книга Шеннона, многие книги по теории кодирования), у нас по инерции теорию информации причислили к спецдисциплинам со всеми вытекающими отсюда последствиями: секретными тетрадями и подготовкой в спецбоксе (совместно с преферансом).

Весь четвертый курс был посвящен практически одним спецдисциплинам. Все самые зверские экзамены (ТВИСТ и алгебра) остались позади, на экзаменах по СД уже обстановка была намного спокойнее, никого, как правило, за них не выгоняли, двойки ставили редко. Пахло окончанием факультета.

Оглавление книги