Книга: Графика DirectX в Delphi

Глава 9 Трехмерные построения

Глава 9 Трехмерные построения

Матричный подход

Реалистичные изображения

Буфер глубины

Подготовка моделей

Что вы узнали в этой главе

Предлагаемый материал во многом основан на сведениях предыдущей главы, но имеет принципиальное отличие: в ней мы переходим к трехмерной графике.

Такой переход потребует небольшого экскурса в линейную алгебру. В остальном же знакомство с новой темой потребует изучения методов объектов, связанных с 3D графикой.

Примеры, рассматриваемые в данной главе, располагаются в каталоге ExamplesChapter09.

Матричный подход

Прежде, чем мы приступим к рисованию в пространстве, нам предстоит поговорить о некоторых важных вещах, обойти которые невозможно, хотя они напрямую, казалось бы, и не связаны с программированием.

Вкратце повторим подходы, используемые нами в предыдущих главах, посвященных Direct3D. Буфер вершин заполняется данными некоторого формата об опорных вершинах, образующих примитивы. Если примитивы должны перемещаться по экрану, буфер вершин заполняется новыми данными. Для поворота объекта надо запереть буфер, чтобы получить доступ к его содержимому, и заполнить буфер новыми данными.

В трехмерных построениях мы будем избегать такого подхода. Использованные нами ранее форматы данных о вершинах содержат три пространственные координаты, и нетрудно догадаться, что для перехода к трехмерной графике надо для начала задействовать Z-координату, ранее нами игнорируемую. Конечно, потребуются еще некоторые действия, но интуиция подсказывает, что для рисования, например, кубика, надо построить треугольники, образующие стороны куба, манипулируя значением третьей координаты. А для того, чтобы нарисовать вращающийся кубик, следует периодически обновлять содержимое буфера вершин. Но мы сразу же должны оговориться, что было бы лучше, если бы мы один раз заполняли буфер данными о кубике, а воспроизводили его каждый раз немного повернутым относительно предыдущего положения. Конечно, это оптимально: заполнить буфер один раз массивом данных об объектах сцены, а при воспроизведении каждого объекта выполнять менее требовательные к ресурсам операции, указывая его текущее положение в пространстве. К такому порядку действий мы и будем стремиться. Не использовал я такого подхода раньше только потому, что боялся нагрузить вас обилием материала (этого я боюсь и сейчас), и хотел бы, чтобы мы двигались шаг за шагом. Но, к сожалению, сейчас нам придется сделать очень большой скачок, и для того, чтобы не споткнуться, следует утроить внимание. Начнем.

При описании объекта, заполнении буфера вершин опираемся на мировую систему координат. Иными словами, указываем координаты вершин объектов так, как будто все они находятся в точке начала глобальной системы координат.

Объекты трехмерной сцены наделяются системой координат, первоначально совпадающей с мировой системой. Каждая трансформация системы координат, связанной с объектом, приведет к трансформации объекта. Если перед воспроизведением объекта сместить его систему координат, то объект будет рисоваться на новом месте, т. е. относительно смещенной по одной или нескольким осям системы координат. Для осуществления поворота объекта поворачиваем систему координат, связанную с ним, вокруг одной из осей. Если на сцене присутствует несколько объектов, то перед рисованием каждого из них трансформируем систему координат, ассоциированную с этим объектом.

Надеюсь, пока все понятно и просто, и мы можем поговорить о том, как собственно осуществлять манипуляции с системой координат объекта. Самыми популярными математическими методами для описания таких преобразований служат векторный и матричный. Трехмерная графика базируется, как правило, на матричном подходе, заключающемся в том, что операции с системой координат основываются на матричном представлении. Базовым элементом матричного метода является матрица (таблица чисел) размером 4x4. Я знаю первый вопрос, который возникает всегда и у всех, кто впервые слышит о матричном методе: почему размер матрицы именно такой. В математике для описания точки в пространстве используется четыре числа, вспомогательной характеристике можно придать любой смысл, это может быть, например, заряд частицы или материальная масса. В графике четвертый компонент координаты точки называется W-координатой и предназначен для осуществления проекции точки на плоскость экрана. Это весовой фактор, на который умножаются координаты точки при ее проецировании. Его значение задается единичным.

Основной операцией, к которой прибегают при манипуляции с матрицами, является перемножение матриц, осуществляемое по формуле:

Количество строк перемножаемых матриц должно быть одинаковым.

При умножении матрицы на вектор первым множителем слагаемых суммы берутся последовательно элементы единственного столбца вектора.

Единичная матрица, т. е. матрица, по главной диагонали которой располагаются единицы, а все остальные элементы равны нулю, соответствует мировой системе координат. Другое название такой матрицы - матрица идентичности, после умножения ее на вектор получается исходный вектор.

Матрицы сдвига по осям X, Y и Z выглядят так:

Если умножить вектор (X, У, Z, W) на матрицу сдвига по оси X, в результате получится вектор (X + W o a, Y, Z, W). Умножение вектора координат всех точек объектов на матрицу сдвига приводит к перемещению объекта по нужной оси.

Три матрицы сдвига можно объединить в одну, дающую возможность осуществлять сдвиг одновременно по нескольким осям. Последняя строка такой матрицы имеет ненулевые значения в столбцах, соответствующих нужным осям.

Возвращаясь в Direct3D, поясню: у объекта устройства есть метод, позволяющий задать матрицу, на которую будут умножаться векторы координат вершин непосредственно перед отображением в пространстве. И пока в качестве такой матрицы указана матрица сдвига, все воспроизводимые объекты будут сдвигаться в пространстве.

Аналогично сдвигу, операции поворота описываются матрицами. Для поворота на угол а вокруг оси X вектор координат вершины надо умножить на такую матрицу:

Если же надо повернуть на угол (3 вокруг оси Y, то пользуются такой матрицей:

И последняя ситуация с поворотом: угол у, поворот вокруг оси Z:

Чтобы осуществить одновременный поворот по нескольким осям либо скомбинировать поворот и сдвиг, надо применить в качестве трансформаций произведение нужных матриц. При этом важен порядок, в котором мы перемножаем матрицы, он определяет последовательность трансформаций системы координат.

Операции с объектами осуществляются в трехмерном пространстве, описываемом матрицей, которую будем называть мировой матрицей. Помимо мировой матрицы требуется указать видовую матрицу, соответствующую позиции глаза наблюдателя и направлению, в котором он смотрит. В принципе, ее можно задавать точно так же, как и мировую, используя матрицы сдвига и поворота.

Последняя матрица, которая нужна для получения проекции трехмерной сцены на экране, так и называется - матрицей проекции. Значения элементов этой матрицы задают правила, согласно которым будет осуществляться проецирование: положение задней и передней отсекающих плоскостей, искажения, имитирующие перспективу (рис. 9.1).

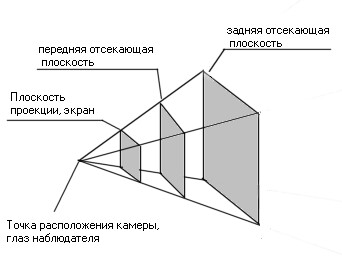
Объекты, или части объектов, располагающиеся за пределами области видимости, на экран проецироваться не будут, и мы их не увидим.

Итак, мы бросили беглый взгляд на сухой теоретический материал, из которого вынесли тяжелое подозрение, что впереди нас ожидает бурелом кодирования математических формул. Отчасти это правда. Direct3D оставил программисту тяготы перемножения матриц, ожидая от него три результирующие матрицы трансформаций. Однако мы воспользуемся модулем Dxcutiis, который содержит набор полезных функций. Автор переноса на Delphi кода этих функций указан в заголовке модуля.

В списке подключаемых модулей первого примера этой главы, проекте каталога Ex01, как раз и добавлен указанный модуль. Пример очень простой, в пространстве вращаются два объекта: разноцветный треугольник и желтый квадрат (рис. 9.2).

Чтобы при вращении примитивов мы могли видеть обе их стороны, режим отсечения отключается, а для использования окрашенных примитивов запрещена работа с источником света:

with FDBDDevice do begin

SetRenderState(D3DRS_CULLMODE, D3DCULL_HONE);

SetRenderState(D3DRS_LIGHTING, DWORD (False)); end;

Буфер вершин запирается один раз. Семь вершин содержат координаты треугольника и квадрата. Если бы они выводились не трансформируемыми, то накладывались бы друг на друга:

Vertices.X := 0.0; // Первая вершина треугольника

Vertices.Y := 1.0;

Vertices.Z := 0.0;

Vertices.Color := $00FF0000;

Inc(Vertices);

Vertices.X := 1.0; // Вторая вершина треугольника

Vertices.Y := -1.0;

Vertices.Z := 0.0;

Vertices.Color := $0000FF00;

Inc(Vertices);

Vertices.X := -1.0; // Третья вершина треугольника

Vertices.Y := -1.0;

Vertices.Z := 0.0;

Vertices.Color := $000000FF;

Inc(Vertices);

Vertices.X := -1.0; // Первая вершина квадрата

Vertices.Y := -1.0;

Vertices.Z := 0.0;

Vertices.Color := $00FFFF00;

Inc(Vertices);

Vertices.X := -1.0; // Вторая вершина квадрата

Vertices.Y := 1.0;

Vertices.Z := 0.0;

Vertices.Color := $00FFFF00;

Inc(Vertices);

Vertices.X := 1.0; // Третья вершина квадрата

Vertices.Y := -1.0;

Vertices.Z := 0.0;

Vertices.Color := $00FFFF00;

Inc(Vertices);

Vertices.X := 1.0; // Четвертая вершина квадрата

Vertices.Y := 1.0;

Vertices.Z := 0.0;

Vertices.Color := $00FFFF00;

При каждой перерисовке кадра вызывается процедура:

procedure TfrmD3D.DrawScene;

var

matView, matProj : TDSDMatrix; // Матрицы 4x4

matRotate, matTranslate : TDSDMatrix;

begin

// Получить матрицу поворота вокруг оси X

SetRotateXMatrix(matRotate, Angle); // Матрица сдвига по оси X, на единицу влево

SetTranslateMatrix(matTranslate, -1.0, 0.0, 0.0); // Устанавливаем мировую матрицу трансформаций FDSDDevice.SetTransform(D3DTS_WORLD,

MatrixMul(matRotate, matTranslate)); // Выводится треугольник

FD3DDevice.DrawPrimiti.ve(D3DPTJTRIANGLELIST, 0, 1); // Квадрат вращается по оси Y в 2 раза быстрее треугольника SetRotateYMatrix(matRotate, 2 * Angle); // Квадрат сдвигается на единицу вправо

SetTranslateMatrix(matTranslate, 1.0, 0.0, 0.0); // Матрица трансформаций для квадрата

FD3DDevice.SetTransform(D3DTS_WORLD,

MatrixMul(matTranslate, matRotate)); // Вывод квадрата

FD3DDevice.DrawPrimitive(D3DPT_TRIANGLESTRIP, 3, 2); // Задаем видовую матрицу

SetViewMatrix(matView, D3DVector(0, 0, -5),

D3DVector(0, 0, 0), D3DVector(0, 1, 0)); // Устанавливаем видовую матрицу

FD3DDevice.SetTransform(D3DTS_VIEW, matView); // Задаем матрицу проекций

SetProjectionMatrix(matProj, I, 1, 1, 10); // Устанавливаем матрицу проекций

FD3DDevice.SetTransform(D3DTS_PROJECTION, matProj);

end;

Тип TD3DMatrix, массив 4x4 вещественных чисел, определен в модуле DirectxGraphics, а все функции операций с матрицами - в модуле DXGUtils. Эти функции возвращают величину типа HRESULT, значение которой мы, для простоты, анализировать не будем.

Функция D3DVector этого же модуля возвращает сформированный по трем аргументам вектор, тройку вещественных чисел, величину типа TD3DVector.

Функция SetRotateXMatrix первым аргументом получает переменную, в которую помещается результат, матрицу поворота вокруг оси X. Второй аргумент - угол, в радианах, на который осуществляется поворот. Функция SetTranslateMatrix первым аргументом получает переменную, в которую помещается заполненная матрица сдвига. Одновременно можно сдвинуть по нескольким осям.

Метод setTransform объекта устройства позволяет установить матрицу трансформаций. Первый аргумент - константа, определяющая, для какой матрицы устанавливается трансформация. Второй аргумент - собственно матрица трансформаций. Здесь мы передаем результирующую матрицу, полученную умножением матрицы поворота и матрицы сдвига, но не обязательно, чтобы в трансформации участвовало несколько матриц. Функция MatrixMul позволяет умножить две матрицы, передаваемые в качестве параметров.

Напоминаю, что порядок перечисления этих матриц очень важен. В данном случае разноцветный треугольник поворачивается вокруг оси X, затем сдвигается на единицу влево, по этой же оси.

Квадрат в этом примере вначале сдвигается вправо, затем поворачивается вокруг оси Y (собственной оси, а не мировой). Измените порядок перемножения матриц, чтобы убедиться, что результат будет отличаться от предыдущего.

Функция setviewMatrix подготавливает видовую матрицу. Параметры функции следующие: матрица, в которую помещается результат, вектор, определяющий точку, где располагается голова наблюдателя, опорная точка, определяющая середину видимой области, и вектор, задающий направление взгляда.

Функция setProjectionMatrix предназначена для удобного определения матрицы проекции. Второй аргумент функции задает угол обзора камеры по оси Y, третий аргумент - отношение, определяющее угол обзора по оси X, последние два аргумента - расстояния от глаза наблюдателя до ближней и дальней плоскостей отсечения.

Подозреваю, что последние две функции вызовут много вопросов, поэтому чуть позже мы подробно разберем их смысл. Пока же мы должны только помнить, что смотрим на сцену со стороны оси Z, и находимся от точки отсчета системы координат на расстоянии 5 единиц.

Реалистичные изображения

Для получения реалистичных изображений необходимо выполнить три условия:

* при описании примитивов задать нормали; определить свойство материала; включить источник света.

Нормали помогают системе рассчитать освещенность примитива при различном его положении относительно источника света. В самом простом использовании нормаль представляет собой вектор, перпендикулярный воспроизводимому треугольнику. Этот вектор задается для каждой вершины, образующей примитив, и из требований оптимизации должен быть нормализован, т. е. иметь единичную длину.

Формат вершин теперь помимо пространственных координат обязан включать вектор нормали (тройку вещественных чисел), а FVF-флаг должен дополниться константой D3DFVF_NORMAL. ЭТО первое новшество в модуле нашего следующего примера, проекта каталога Ех02, где рисуется красивый желтый кубик (рис. 9.3).

Итак, запись описания вершины дополнилась тремя полями:

type

TCUSTOMVERTEX = packed record

X, Y, Z : Single;

nX, nY, nZ : Single; // Вектор нормали end;

const

D3DEVF_CUSTOMVERTEX = D3DFVF_XYZ or D3DFVF_NORMAL;

Буфер содержит 36 вершин, предназначенных для построения куба. Они образуют 12 независимых треугольников, по 2 соприкасающихся треугольника на каждую сторону куба. Все треугольники описываются по часовой стрелке, чтобы при воспроизведении мы могли, для экономии времени, отключить воспроизведение примитивов, перечисляемых в поле зрения против часовой стрелки. То есть стороны куба, повернутые к нам задней стороной, воспроизводить не будем, это обычный прием, применяемый к замкнутым трехмерным фигурам. Нормали для всех вершин, относящихся к одной стороне, задаются одинаковыми, исходя из того, какая сторона куба описывается. Так выглядит описание первого треугольника:

Vertices.X := -0.5;

Vertices.Y := -0.5;

Vertices.Z := -0.5;

Vertices.nX := -1.0;

Inc(Vertices);

При инициализации графической системы вызывается процедура, задающая свойства материала и включающая источник света:

procedure TfrmD3D.SetupLights;

var

Material : TD3DMaterial8;

Light : TD3DLight8;

begin

// Инициализация материала, желтый цвет

Material := InitMaterial(1, 1, 0, 0) ;

// Устанавливаем материал в объекте устройства

FD3DDevice.SetMaterial(Material);

// Инициализация направленного источника, белый свет

Light := InitDirectionalLight(DSDVector(0, 0, 1), 1, 1, 1, 0) ;

// Устанавливаем источник света

FDSDDevice.SetLight(0, Light);

// Включаем источник света

FD3DDevice.LightEnable(0, True);

end;

Материал и источник света являются записями (не СОМ-объекты) и имеют тип TD3DMateriais и TD3DLight8 соответственно. Пользовательская функция InitMaterial заполняет поля структуры материала и получает в качестве аргументов значения ARGB. Отличает эти параметры от привычного их использования, помимо порядка, в котором они перечисляются, то, что это вещественные числа, единица соответствует максимальному значению аргумента.

В примере материал задается желтым, для того, чтобы установить его. При этом используется метод SetMaterial объекта устройства.

Функция InitDirectionalLight заполняет поля структуры, описывающей направленный источник света. Первым аргументом передается вектор, задающий направление лучей света. Напоминаю, что мы наблюдаем сцену с отрицательной стороны оси Z. Чтобы лучи света были параллельны нашему взору, вектор направления задается (0, 0, 1). Следующие три аргумента описывают цветовой фильтр, накладываемый на источник света, обычно источник задается белым. Эти числа также вещественны. Значение последнего аргумента для направленного источника безразлично.

Метод setLight объекта устройства устанавливает источник света на сцене. Первый аргумент, целое число, основанное на нуле, является индексом, идентификатором источника света. Метод только задает источник света, включается же он с помощью отдельного метода, LightEnabie, первый аргумент которого - индекс нужного источника, второй аргумент - булево выражение.

Как я уже говорил, отключается воспроизведение задних сторон треугольников, т. е. тех, чьи вершины перечисляются против часовой стрелки:

SetRenderState(D3DRS__CULLMODE, D3DCULL_CCW);

Совсем не обязательно, чтобы вершины примитива перечислялись именно по часовой стрелке, можно использовать и противоположное направление. Просто желательно, чтобы существовал какой-нибудь определенный порядок перечисления, чтобы можно было отсекать воспроизведение задних сторон. Повторюсь, внутренние стороны кубика нам не видны в любом случае, поэтому и незачем тратить время на их воспроизведение. Также обращаю ваше внимание на то, что связанные треугольники приспособлены для перечисления вершин именно по часовой стрелке.

Есть и еще один важный аспект, который нам необходимо учитывать: DirectSD не может окрашивать примитивы с двух сторон. Замените последний аргумент метода Drawprimitive на 2 и установите значение для режима D3DRs_CULLMODE в D3DCULL_NONE. Теперь будет выводиться только одна сторона куба, отсечение задней стороны примитивов не производится. Обратите внимание, что когда квадрат поворачивается к зрителю задней стороной, он выводится черным, т. е. совершенно не окрашиваемым.

Кубик в нашем примере вращается вокруг двух осей одновременно:

SetRotateXMatrix(matRotateX, Angle);

SetRotateYMatrix(matRotateY, Angle);

FD3DDevice.SetTransform(D3DTS_WORLD, MatrixMul(matRotateX, matRotateY));

FD3DDevice.DrawPrimitive(D3DPT__TRIANGLELIST, 0, 12);

На рисунке куб получился крупнее, чем при работе приложения. Для того, чтобы увеличить изображение, можно просто "приблизить" глаз наблюдателя:

SetViewMatrixfmatView, D3DVector(0, 0, -2),

D3DVector(0, 0, 0), D3DVector(0, I, 0));

Есть и другой способ: действительно увеличить объект. Для этого в матрицу трансформаций надо добавить матрицу масштабирования, по главной диагонали которой стоят числа, отличные от единицы и равные масштабным множителям по трем осям отдельно. Попробуйте сейчас увеличить кубик в два раза:

procedure TfrmD3D.DrawScene;

var

matView, matProj : TD3DMatrix;

matRotateX, matRotateY : TD3DMatrix;

niatScale : TD3DMatrix; // Добавилась матрица масштабирования

begin

SetRotateXMatrix(matRotateX, Angle);

SetRotateYMatrix(matRotateY, Angle);

SetScaleMatrix(matScale, 2.0, 2.0, 2.0); // Увеличиваем в 2 раза

// Добавляем матрицу масштабирования

FD3DDevice.SetTransform(D3DTS_WORLD, MatrixMul(matScale,

MatrixMul(matRotateX, matRotateY)));

Обязательно это сделайте, чтобы увидеть, что куб действительно увеличился. Однако освещение его тоже изменилось. Связано это с тем, что векторы нормалей к вершинам вслед за масштабированием стали увеличенными, и требуется их нормализация. В таких случаях необходимо включить режим автоматической нормализации этих векторов:

SetRenderState(D3DRS NORMALIZENORMALS, DWORD (True));

Буфер глубины

Продолжим рассмотрение нашего примера с вращающимся кубом. В нем еще остались некоторые новые для нас вещи. Рисуемые примитивы накладываются друг на друга в том порядке, в котором они воспроизводятся: нарисованные позже лежат поверх созданных ранее. Это хорошо для двумерных построений, но при переходе в ЗD-пространство нам приходится беспокоиться о том, чтобы положения объектов передавались правильно: более удаленные от глаза наблюдателя объекты могут заслонять воспроизведенные позже, но располагающиеся ближе к камере. Графическая система предлагает решение в виде использования буфера глубины - вспомогательного экрана, предназначенного только для сортировки объектов, располагающихся в пространстве. При подключении этого буфера воспроизведение осуществляется дважды: первый раз в буфер записывается информация о значении расстояния от камеры до точки, второй раз в буфер кадра помещаются данные только о точках, действительно видимых и не заслоняемых другими точками.

Другое название буфера глубины - Z-буфер.

При инициализации Direct3D надо указать, что будет использоваться буфер глубины, и задать его формат. Обычно используется 16-битный формат:

with d3dpp do begin

Windowed := True;

SwapEffect := D3DSWAPEFFECT_DISCARD;

BackBufferFormat := dSddm.Format;

// Будет использоваться буфер глубины

EnableAutoDepthStencil := True;

AutoDepthStencilFormat := D3DFMT_D16; // 16-битный формат

end;

Размеры буфера глубины будут автоматически определяться системой при каждом изменении размеров окна.

При очередной перерисовке кадра теперь должен очищаться не только буфер кадра, но и подключенный буфер глубины. Предпоследний параметр метода clear объекта устройства - значение, которым заполняется буфер глубины. Этим значением должна быть единица, фон экрана бесконечно удален в пространстве:

FD3DDevice.Clear(0, nil, D3DCLEAR_TARGET or D3DCLEAR_ZBUFFER,

$00FFFFFF, 1.0, 0) ;

Для разрешения работы с буфером глубины надо также задать положительный флаг для соответствующего режима:

SetRenderState(D3DRS_ZENABLE, D3DZBJTRUE);

Флагом для этого состояния может быть и обычная булева константа.

Сейчас нам необходимо перейти к следующему примеру, проекту каталога Ех03, после его запуска на экране появляется вращающийся чайник и стрелки осей координат (рис. 9.4).

Буфер вершин заполняется данными для трех трехмерных объектов: цилиндра, конуса и чайника:

function TfrmD3D.InitVB : HRESULT;

const

radius =0.1; // Радиус цилиндра

var

Vertices : ^TCustomVertex;

hRet : HRESULT;

theta : Single;

i : Integer;

t : TextFile; // Данные модели хранятся в текстовом файле

wX, wY, wZ : Single;

egin hRet := FD3DDevice.CreateVertexBuffer((100 + 51 * 2 + 6322 * 3) *

SizeOf(TCustomVertex), 0, D3DFVF_CUSTOMVERTEX, D3DPOOL_DEFAULT, FD3DVB);

if Failed(hRet) then begin

Result := hRet;

Exit;

end;

hRet := FDSDDevice.SetStreamSource(0, FD3DVB, SizeOf(TCustomVertex));

if Failed(hRet) then begin

Result := hRet;

Exit;

end;

hRet := FD3DDevice.SetVertexShader(D3DFVF_CUSTOMVERTEX);

if Failed(hRet) then begin

Result := hRet;

Exit; end; hRet := FD3DVB.Lock(0, (100 + 51 * 2 + 6322 * 3)*

SizeOf(TCustomVertex), PByte(Vertices), 0);

if Failed(hRet) then begin

Result := hRet;

Exit;

end;

// 100 вершин цилиндра, по часовой стрелке

for i ;= 49 downto 0 do begin

theta := 2 * Pi * i / 49;

Vertices.X := sin(theta) * radius;

Vertices.Y := -1;

Vertices.Z := cos(theta) * radius;

Vertices.nX := sin(theta);

Vertices.nY := 0;

Vertices.nZ := cos(theta);

Inc(Vertices);

Vertices.X := sin(theta) * radius;

Vertices.Y := 1;

Vertices.Z := cos(theta) * radius;

Vertices.nX := sin(theta);

Vertices.nY := 0;

Vertices.nZ := cos(theta);

Inc(Vertices);

end;

// Вершина конуса

Vertices.X := 0.0;

Vertices.Y := 0.0;

Vertices.Z := 1.0;

Vertices.nX := 0.0;

Vertices.nY := 0.0;

Vertices.nZ := 1.0;

Inc(Vertices) ;

// Треугольники, образующие конус

for i := 0 to 49 do begin

theta := 2 * Pi * i / 49;

Vertices.X := cos(theta);

Vertices.Y := sin(theta);

Vertices.Z := 0.0;

Vertices.nX := cos(theta);

Vertices.nY := sin(theta);

Vertices.nZ := 1.0;

Inc(Vertices);

end;

// Центр донышка конуса

Vertices.X := 0.0;

Vertices.Y := 0.0;

Vertices.Z := 0.0;

Vertices.nX := 0.0;

Vertices.nY := 0.0;

Vertices.nZ := -1.0;

Inc(Vertices);

// Круг, закрывающий конус

for i := 0 to 49 do begin

theta := 2 * Pi * i / 49;

Vertices.X := sin(theta);

Vertices.Y := cos(theta);

Vertices.Z := 0.0;

Vertices.nX := 0.0;

Vertices.nY := 0.0;

Vertices.nZ := -1.0;

Inc(Vertices);

end;

// Считьшаем данные модели из файла

AssignFile (t, 'teapot.txt');

Reset (t) ;

while not EOF(t) do begin

Readln (t, wX); // Нормаль к треугольнику

Readln (t, wY);

Readln (t, wZ) ;

Readln (t, Vertices.X); // Первая вершина треугольника

Readln (t, Vertices.Y);

Readln (t, Vertices.Z);

Vertices.nX := wX;

Vertices.nY := wY;

Vertices.nZ := wZ;

Inc (Vertices);

Readln (t, Vertices.X); // Вторая вершина треугольника

Readln (t, Vertices.Y);

Readln (t, Vertices.Z);

Vertices.nX := wX;

Vertices.nY := wY;

Vertices.nZ := wZ;

Inc (Vertices);

Readln (t, Vertices.X) ; // Последняя вершина треугольника

Readln (t, Vertices.Y);

Readln (t, Vertices.Z);

Vertices.nX := wX;

Vertices.nY := wY;

Vertices.nZ := wZ;

Inc (Vertices); end;

CloseFile (t); Result := FD3DVB.Unlock;

end;

Цилиндр радиуса 0.1 и высотой 2 строится вокруг оси Y, а конус единичной высоты - вокруг оси Z. О том, как получены точки модели, мы поговорим чуть позже, сейчас же я должен сообщить, что вершины треугольников модели перечисляются против часовой стрелки.

Текущие параметры матриц вида и проекций хранятся в следующих переменных:

FromX, FromY, FromZ : Single;

AtX, AtY, AtZ : Single;

WorldUpX, WorldUpY, WorldUpZ : Single;

fFOV, fAspect, fNearPlane, fFarPlane : Single;

Инициализируются эти переменные значениями, такими же, как в предыдущих примерах, лишь точка зрения отодвинута на единицу:

procedure TfrmDSD.FormCreate(Sender: TObject);

var

hRet : HRESULT;

begin

hRet := InitD3D;

if Failed (hRet) then ErrorOut (4nitD3D'f hRet);

hRet := InitVB;

if Failed (hRet) then ErrorOut ('InitVertex', hRet);

// Включаем источники света и инициализируем материалы

SetupLights;

MaterialRed := InitMaterial(1, 0, 0, 1);

MaterialBlue := InitMaterial(0, 0,1, 1);

MaterialGreen := InitMaterial(0, 1, 0, 1) ;

MaterialYellow := InitMaterial(1, 1, 0, 1);

FromX := 0.0; // Вектор "From"

FromY := 0.0;

FromZ := -6.0;

AtX := 0.0; // Вектор "At"

AtY := 0.0;

AtZ := 0.0;

WorldUpX := 0.0; // Вектор "WorldUp"

WorldUpY := 1.0;

WorldUpZ := 0.0;

fFOV := 1.0; // Угол обзора по оси Y

fAspect := 1.0; // Угол обзора по оси X

fNearPlane := 1.0; // Передняя плоскость отсечения

fFarPlane := 20; // Задняя плоскость отсечения

end;

Для повышения красочности на сцене присутствует два источника света:

procedure TfrmDSD.SetupLights;

var

LightO : TD3DLight8;

Lightl : TD3DLight8;

begin

LightO := InitDirectionalLight(D3DVector(-1, -1, -1), 1, 1, 1, 0);

FDSDDevice.SetLight (0, LightO);

Lightl := InitDirectionalLight(D3DVector(0, 0, 1), 1, 1, 1, 0);

FDSDDevice.SetLight (1, Lightl);

FD3DDevice.LightEnable (0, True);

FD3DDevice.LightEnable (1, True);

end;

При воспроизведении объектов сцены параметры матриц вида и проекций опираются на текущие значения управляющих переменных:

procedure TfrmDSD.DrawScene;

var

matView, matProj : TD3DMatrix;

matRotate, matTranslate : TDSDMatrix;

matRotateX, matRotateY : TD3DMatrix;

matScale : TD3DMatrix;

begin

// Цилиндр по оси X

SetRotateZMatrix(matRotate, Pi / 2);

SetTranslateMatrix(matTranslate, 1.0, 0.0, 0.0);

with FD3DDevice do begin

SetRenderState(D3DRS_CULLMODE, D3DCULL_CCW);

SetTransform(D3DTS_WORLD, MatrixMul(matTranslate, matRotate));

SetMaterial(MaterialRed); // Красного цвета

DrawPrimitive(D3DPT_TRIANGLESTRIP, 0, 50 * 2 - 2);

end;

// Конус стрелки по оси Z

SetRotateYMatrix(matRotate, Pi / 2);

SetTranslateMatrix(matTranslate, 2.0, 0.0, 0.0);

SetScaleMatrix(matScale, 1.0, 0.5, 0.5);

with FDSDDevice do begin

SetTransform(D3DTS_WORLD, MatrixMul(matScale,

MatrixMul(matTranslate, matRotate)));

DrawPrimitive(D3DPT_TRIANGLEFAN, 100, 49); // Сам конус

DrawPrimitive(D3DPT_TRIANGLEFAN, 151, 50); // Донышко конуса

end;

// Цилиндр по оси Y

SetTranslateMatrix(matTranslate, 0.0, 1.0, 0.0);

with FDSDDevice do begin

SetTransform(D3DTS__WORLD, matTranslate);

SetMaterial(MaterialGreen); // Цвет - зеленый

DrawPrimitive(D3DPT_TRIANGLESTRIP, 0, 50 * 2 - 2);

end;

// Конус стрелки по оси Y SetRotateXMatrix(matRotate, -Pi / 2);

SetTranslateMatrix(matTranslate, 0.0, 2.0, 0.0);

SetScaleMatrix(matScale, 0.5, 1.0, 0.5);

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, MatrixMul(matScale,

MatrixMul(matTranslate, matRotate)));

DrawPrimitive(D3DPT_TRIANGLEFAN, 100, 49);

DrawPrimitive(D3DPT_TRIANGLEFAN, 151, 50);

end;

// Цилиндр по оси Z

SetRotateXMatrix(matRotate, Pi / 2) ;

SetTranslateMatrix(matTranslate, 0.0, 0.0, 1.0);

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, MatrixMul(matTranslate, matRotate));

SetMaterial(MaterialBlue); // Синего цвета

DrawPrimitive(D3DPT_TRIANGLESTRIP, 0, 50 * 2 - 2);

end;

// Конус стрелки по оси Z

SetTranslateMatrix(matTranslate, 0.0, 0.0, 2.0);

SetScaleMatrix(matScale, 0.5, 0.5, 1.0); with FD3DDevice do begin

SetTransform(D3DTS_WORLD, MatrixMul(matScale, matTranslate));

DrawPrimitive(D3DPT_TRIANGLEFAN, 100, 49);

DrawPrimitive(D3DPT_TRIANGLEFAN, 151, 50);

end;

// Чайник, вращающийся вокруг осей X и Y

SetRotateXMatrix(matRotateX, Angle);

SetRotateYMatrixfmatRotateY, Angle);

SetTranslateMatrix(matTranslate, 0.0, -1.5, 0.0);

SetScaleMatrix(matScale, 0.5, 0.5, 0.5); // Уменьшаем в два раза

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, MatrixMul(matRotateX, MatrixMul(matRotateY, MatrixMul(matScale, matTranslate))));

SetMaterial(MaterialYellow);

// Вершины модели перечисляются против часовой стрелки

SetRenderState(D3DRS_CULLMODE, D3DCULL_CW);

DrawPrimitive(D3DPT_TRIANGLELIST, 100 + 51 * 2, 6322);

end;

// Матрица вида

SetViewMatrix(matView, DSDVector(FromX, FromY, FromZ),

D3DVector(AtX, AtY, AtZ), DSDVector(WorldUpX, WorldUpY, WorldUpZ));

FD3DDevice.SetTransform(D3DTS_VIEW, matView); // Матрица проекций

SetProjectionMatrix(matProj, fFOV, fAspect, fNearPlane, fFarPlane);

FD3DDevice.SetTransform(D3DTS_PROJECTION, matProj);

end;

Поначалу, наверняка, вам будет тяжело разбирать последовательности манипуляций с матрицами при воспроизведении нескольких объектов. Для приобретения опыта попробуйте решить простейшие задачи, например удлините цилиндры и конусы осей.

Но главное предназначение этого примера - разрешить все возможные вопросы об установках матриц вида и проекций. По нажатии клавиши <Пробел> появляется вспомогательное окно, в полях редактирования которого выводится текущее значение управляющих переменных:

procedure TfrmDSD.FormKeyDown(Sender: TObject; var Key: Word;

Shift: TShiftState);

begin

if Key = VKJESCAPE then Close else

if Key = VK_SPACE then with Form2 do begin

edtFromX.Text := FloatToStr (FromX);

edtFromY.Text := FloatToStr (FromY);

edtFromZ.Text := FloatToStr (FromZ);

edtAtX.Text := FloatToStr (AtX);

edtAtY.Text := FloatToStr (AtY) ;

edtAtZ.Text := FloatToStr (AtZ);

edtWorldUpX.Text := FloatToStr (WorldUpX);

edtWorldUpY.Text := FloatToStr (WorldUpY);

edtWorldUpZ.Text := FloatToStr (WorldUpZ);

edtFOV.Text := FloatToStr (fFOV);

edtAspect.Text := FloatToStr (fAspect);

edtNearPlane.Text := FloatToStr (fNearPlane);

edtFarPlane.Text := FloatToStr (fFarPlane);

Show;

end;

end;

Первоначально мы видим только две оси: стрелка оси Z закрыта вращающейся моделью. Меняя значения координат вектора "From", мы передвигаем точку обзора - координаты той точки в пространстве, где находится глаз наблюдателя. Вектор "At" определяет точку, находящуюся в середине сцены. Если здесь задавать отличные друг от друга значения, то наша композиция будет перемещаться по плоскости экрана, т. е. этот вектор соответствует направлению взгляда наблюдателя. Вектор "WorldUp" указывает направление и величину поворота головы. Если менять значения его составляющих, оси нашей сцены начнут "меняться местами".

Значение FOV задает величину производимого увеличения в радианах. Чем меньше это число, тем крупнее выглядит наша картинка. Обратите внимание, что сами объекты при этом не перемещаются, мы как будто просто вращаем колесико настройки бинокля. Значение величины Aspect определяет степень сжатия картинки по горизонтали: чем больше это число, тем сильнее растягивается изображение. Обычно здесь передается отношение ширины окна к его высоте.

Расстояния до передней и задней плоскостей отсечения задают видимую область пространства. Расстояния отмеряются от глаза наблюдателя. Все точки, выходящие за пределы этой области, не воспроизводятся. Из соображений оптимизации плоскости сечения располагаются максимально близко друг к другу, чтобы сократить время вычислений. Обратите внимание, это очень важно: нельзя устанавливать нулевым значение расстояния до передней плоскости отсечения. Такое значение равносильно отказу от использования буфера глубины.

Надеюсь, неспешная работа с этим примером позволит вам хорошо разобраться с матрицами, определяющими вид картинки.

Подготовка моделей

Конусы и цилиндры, сфера и правильные многогранники - все подобные геометрические фигуры легко описываются и могут украсить вашу программу. Пример - проект каталога Ех04, в котором рисуется икосаэдр (рис. 9.6).

Этот многогранник описан двадцатью независимыми треугольниками. Координаты вершин и нормали я предварительно вычислил и использую в программе конкретные значения.

Знаний, которые мы уже получили, достаточно, чтобы создать более-менее интересные построения. Пример - проект каталога Ех05, где рисуется простая модель человечка. Используются две геометрические формы: цилиндр и икосаэдр. С помощью клавиш перемещения курсора конечностями человечка можно управлять, заставляя его поднимать и опускать руки и ноги, но нельзя заставить поднять обе ноги одновременно (рис. 9.7).

Для построения ног применяются цилиндры единичной длины, руки строятся цилиндрами длиной 0.75 единиц. Движения конечностей осуществляются плавно:

const

INCR = 0.05; // Приращение для углов, задает темп вращения цилиндров

var

Down : BOOL = False; // Флаг, указывающий, нажата ли кнопка мыши

оХ : Integer; // Используются для навигации в пространстве

оУ : Integer;

Angle : Single = 0;

sHeight : Single = 0;

// Левая/правая стороны - с точки обзора зрителя

R_hand_up_angle, // Текущий угол поворота верхней части правой руки

R_hand_down_angle, // Текущий угол поворота нижней части правой руки

L_hand_up_angle, // Углы для частей левой руки

L_hand_down_angle,

R_foot_up_angle, // Углы для частей правой ноги

R_foot_down_angle,

L_foot_up_angle, // Углы поворотов левой ноги

L_foot_down_angle : Single;

R_hand_move, // Флаги перемещений конечностей

L_hand_move,

R_foot_move,

L_foot_move : BOOL;

Данный пример важен тем, что учит, как строить комплексные объекты: части конечностей человечка прикреплены друг к другу. Для построения подобных частей необходимо осуществлять относительные трансформации, поэтому во вспомогательной матрице запоминаем текущую трансформацию системы координат:

procedure TfrmD3D.DrawScene;

var

matRotateX, matRotateZ : TDSDMatrix;

matScale, matTranslate : TD3DMatrix;

matWrk : TD3DMatrix; // Вспомогательная матрица текущей трансформации

begin

Timer; // Пересчет текущих значений углов поворота конечностей

// Икосаэдр головы

SetTranslateMatrix(matTranslate, 0.0, -3.0, 0.0);

// Масштабируем единичный многогранник

SetScaleMatrix (matScale, 0.5, 0.5, 0.5);

matWrk := MatrixMul(matScale, matTranslate);

with FDSDDevice do begin

SetTransform(D3DTS_WORLD, matWrk);

SetMaterial(MaterialYellow); // Желтого цвета

DrawPrimitive(D3DPT_TRIANGLELIST, 0, 20);

end;

// Цилиндры левой ноги

SetTranslateMatrixfmatTranslate, -0.2, 0.0, 0.0);

SetRotateXMatrix(matRotateX, L_foot_up_angle);

// Запоминаем положение верхней части

matWrk := MatrixMul(matTranslate, matRotateX);

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, matWrk);

SetMaterial(MaterialBlue); // Ноги - синего цвета

// Цилиндр единичной длины

DrawPrimitive(D3DPT_TRIANGLESTRIP, 60, 98);

end;

// Перемещаемся к концу цилиндра единичной длины

SetTranslateMatrix(matTranslate, 0.0, 1.0, 0.0);

// Поворот нижней части конечности

SetRotateXMatrix(matRotateX, L_foot_down_angle);

// Трансформации осуществляются относительно предыдущего состояния

// системы координат

matWrk := MatrixMul(matWrk, MatrixMul(matTranslate, matRotateX));

with FD3DDevi do begin

SetTransform(D3DTS_WORLD, matWrk);

DrawPrimitive(D3DPT_TRIANGLESTRIP, 60, 98);

end;

// Правая нога

SetTranslateMatrixfmatTranslate, 0.2, 0.0, 0.0);

SetRotateXMatrix(matRotateX, R_foot_up_angle);

// Запоминаем текущее положение верхней части правой ноги

matWrk := MatrixMul(matTranslate, matRotateX);

with FDSDDevice do begin

SetTransform(D3DTS_WORLD, matWrk);

DrawPrimitive(D3DPT_TRIANGLESTRIP, 60, 98);

end;

// Трансформации в новой системе координат

SetTranslateMatrix(matTranslate, 0.0, 1.0, 0.0);

SetRotateXMatrix(matRotateX, R_foot_down_angle);

// Поворот и сдвиг - относительно текущей трансформации

matWrk := MatrixMul(matWrk, MatrixMul(matTranslate, matRotateX));

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, matWrk);

DrawPrimitive(D3DPT_TRLANGLESTRIP, 60, 98);

end;

// Туловище

// Цилиндр с левой стороны туловища

SetTranslateMatrix(matTranslate, -0.2, 0.0, 0.0);

SetRotateZMatrix(matRotateZ, 5 * Pi / 6) ;

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, MatrixMul(matTranslate, matRotateZ));

SetMaterial(MaterialGreen); // Текущий цвет - зеленый

DrawPrimitive(D3DPT_TRJANGLESTRIP, 60, 98);

end;

// Цилиндр правой части туловища

SetTranslateMatrix(matTranslate, 0.2, 0.0, 0.0);

SetRotateZMatrix(matRotateZ, -5 * Pi / 6);

FD3DDevice.SetTransform(D3DTS_WORLD,

MatrixMul(matTranslate, matRotateZ));

FD3DDevice.DrawPrimitive(D3DPT_TRIANGLESTRIP, 60, 98);

// Цилиндр верхней части туловища

SetTranslateMatrix(matTranslate, -1.0, -1.0, 0.0);

SetScaleMatrix (matScale, 1.0, 2.0, 1.0); // Растягиваем цилиндр

SetRotateZMatrix(matRotateZ, Pi / 2);

FD3DDevice.SetTransform(D3DTS_WORLD, MatrixMul(matRotateZ,

MatrixMul(matTranslate, matScale)));

FD3DDevice.DrawPrimitive(D3DPT TRIANGLESTRIP, 60, 98);

// Цилиндр нижней части туловища

SetTranslateMatrix(matTranslate, 0.0, -0.25, 0.0);

SetScaleMatrix (matScale, 1.0, 0.5, 1.0); // Уменьшаем цилиндр

SetRotateZMatrix(matRotateZ, Pi / 2) ;

FD3DDevice.SetTransform(D3DTS_WORLD, MatrixMul(matRotateZ,

MatrixMul(matTranslate, matScale)));

FD3DDevice.DrawPrimitive(D3DPT_TRIANGLESTRIP, 60, 98);

// Левая рука

// Верхняя часть

SetTranslateMatrix(matTranslate, -1.0, -1.0, 0.0);

SetRotateZMatrix(matRotateZ, R_hand_up_angle);

matWrk := MatrixMul(matTranslate, matRotateZ);

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, matWrk);

SetMaterial(MaterialRed); // Текущий цвет - красный

// Цилиндр длиной 0.75

DrawPrimitive(D3DPT_TRIANGLESTRIP, 160, 98);

end;

// Сдвигаемся к концу цилиндра

SetTranslateMatrix(matTranslate, 0.0, 0.75, 0.0);

SetRotateZMatrix(matRotateZ, R_hand_down_angle);

matWrk := MatrixMul(matWrk, MatrixMul(matTranslate, matRotateZ));

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, matWrk);

DrawPrimitive(D3DPT_TRIANGLESTRIP, 160, 98);

end;

// Правая рука

SetTranslateMatrix(matTranslate, 1.0, -1.0, 0.0);

SetRotateZMatrix(matRotateZ, L_hand_up_angle);

matWrk := MatrixMul(matTranslate, matRotateZ);

with FD3DDevice do begin

SetTransform(D3DTS_WORLD, matWrk);

DrawPrimitive(D3DPT_TRIANGLESTRIP, 160, 98);

end;

SetTranslateMatrix(matTranslate, 0.0, 0.75, 0.0);

SetRotateZMatrix(matRotateZ, L_hand_down_angle);

matWrk := MatrixMul(matWrk, MatrixMul{matTranslate, matRotateZ));

with FDSDDevice do begin

SetTransform(D3DTS_WORLD, matWrk);

DrawPrimitive(D3DPT_TRIANGLESTRIP, 160, 98);

end;

end;

При нажатии клавиш управления курсором меняются значения флагов, и наблюдаем мы сцену зеркально.

procedure TfrmD3D.FormKeyDown(Sender: TObject; var Key: Word;

Shift: TShiftState);

begin

if Key = VKJ3SCAPE then Close else

// Клавиша "влево" - правая рука

if Key = VK_LEFT then R_hand_move := not R_hand_move else

// Клавиша "вправо" - левая рука

if Key = VK_RIGHT then L_hand_move := not L_hand_move else

// Клавиша "вверх" - правая нога

if Key = VK_UP then begin

// Двигается, если не поднята левая нога

if L_foot_up_angle < 1.0 then R_foot_move := not R_foot_move;

end else

// Клавиша "вниз" - левая нога

if Key = VK_DOWN then begin

// Двигается, если не поднята правая нога

if R_foot_up_angle < 1.0 then L_foot_move := not L_foot_move;

end;

end;

При установленных флагах значения углов поворотов увеличиваются на величину INCR:

procedure TfrmDSD.Timer;

begin

if R_hand_move then begin // Правая рука поднимается

if R_hand_up_angle < Pi / 2 then begin // He достигнут предел

R_hand_up_angle := R_hand_up_angle + INCR; // Верхняя часть руки

R_hand_down_angle := R_hand_down_angle - INCR; // Нижняя часть

end // Предел достигнут, движется только нижняя часть руки

else if (R_hand_up_angle >= Pi / 2) and (R_hand_down_angle < 0.0)

then R_hand_down_angle := R_hand_down_angle + INCR;

end else // Правая рука опускается или уже опущена

if R_hand_up_angle > 0.0 then begin

R_hand_up_angle := R_hand_up_angle - INCR; if R_hand_down_angle < 0.0

then R_hand_down_angle := R_hand_down_angle + INCR;

end;

if L_hand_move then begin // Левая рука поднимается

if L_hand_up_angle > -Pi / 2 then begin

L_hand_up_angle := L_hand_up_angle - INCR;

L_hand_down_angle := L__hand_down_angle + INCR;

end else if (L_hand_up_angle <= Pi / 2) and (L_hand_down_angle > 0.0)

then L_hand_down_angle := L_hand_down_angle - INCR;

end else if L__hand__up_angle < 0.0 then begin

L_hand_up_angle := L_hand_up_angle + INCR;

if L_hand_down_angle > 0.0

then L_hand_down_angle := L_hand_down_angle - INCR;

end;

if R_foot_move then begin // Правая нога поднимается

if R_foot_up_angle < Pi / 2 then begin

R_foot_up_angle := R_foot__up_angle + INCR;

R_foot_down_angle := R_foot_down_angle - INCR;

end else if (R_foot_up_angle >= Pi / 2) and (R_foot_down_angle < 0.0)

then R_foot_down_angle := R_foot_down_angle + INCR;

end else if R_foot_up_angle > 0.0 then begin

R_foot_up_angle := R_foot_up_angle - INCR; if R_foot_down_angle < 0.0

then R_foot_down_angle := R_foot_down_angle + INCR;

end;

if L_foot_move then begin // Движение левой ноги

if L_foot_up_angle < Pi / 2 then begin

L_foot_up_angle := L_foot_up_angle + INCR;

L_foot_down_angle := L_foot_down_angle - INCR;

end else

if (L_foot_up_angle >= Pi / 2) and (L_foot_down_angle < 0.0)

then L_foot_down_angle := L_foot_down_angle + INCR;

end else

if L_foot_up_angle > 0.0 then begin

L_foot_up_angle := L_foot_up_angle - INCR;

if L_foot_down_angle < 0.0

then L_foot_down_angle := L_foot_down_angle + INCR;

end;

end;

Из этого примера мы также можем вынести для себя механизм удобной навигации в пространстве. Матрица проекций задается один раз, при инициализации:

procedure TfrmD3D.FormCreate(Sender: TObject);

var

hRet : HRESULT;

matView, matProj : TDSDMatrix;

begin

hRet := InitD3D;

if Failed (hRet) then ErrorOut ('InitDSD', hRet);

hRet := InitVB;

if Failed (hRet) then ErrorOut ('InitVertex', hRet);

SetupLights;

MaterialRed := InitMaterial(1, 0, 0, 1);

MaterialBlue := InitMaterial(0, О, 1,1);

MaterialGreen := InitMaterial(О, 1, 0, 1) ;

MaterialYellow := InitMaterial(1, 1, 0, 1) ;

// Первоначальная установка видовой матрицы

SetViewMatrix(matView, D3DVector(2, 1, 5),

D3DVector(0, 0, 0), D3DVector(0, -1, 0));

FD3DDevice.SetTransform(D3DTS_VIEW, matView);

// Матрица проекций задается один раз

SetProjectionMatrix(matProj, 1, 1, 1, 20);

FD3DDevice.SetTransform(D3DTS_PROJECTION, matProj);

end;

Положение точки зрения и параметры матриц я подобрал с помощью пройденного нами примера с осями координат.

При движении курсора мыши с нажатой кнопкой видовая матрица пересчитывается в соответствии с положением курсора:

procedure TfrmDSD.FormMouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

Down := True; // Кнопка нажата, флаг устанавливается

оХ := X; // Запомнили положение курсора

oY := Y;

end;

procedure TfrmD3D.FormMouseUp(Sender: TObject; Button: TMouseButton;

Shift:. TShiftState; X, Y: Integer);

begin

Down : = False; // Кнопка отпущена, флаг сбрасывается

end;

procedure TfrmDSD.FormMouseMove(Sender: TObject; Shift: TShiftState; X,

Y: Integer);

var

eyeX, eyeZ : Single; matView : TD3DMatrix;

begin

if Down then begin // При нажатой кнопке мыши

// Величина перемещения курсора по горизонтали

// задает перемещения точки обзора в пространстве по осям X и Z

Angle := Angle + (X - оХ) / 50.0;

// Перемещение курсора по вертикали задает сдвиг по оси Y

sHeight := sHeight + (У - oY) / 15.0;

eyeX := cos(Angle) * 5;

eyeZ := sin(Angle) * 5;

// Устанавливаем новую видовую матрицу

SetViewMatrixfmatView, D3DVector(eyeX, sHeight, eyeZ),

D3DVector(0, 0, 0), D3DVector(0, -I, 0));

FD3DDevice.SetTransform(D3DTS VIEW, matView);

// Запомнили новое положение курсора

оХ := X;

oY := Y;

end;

end;

В качестве упражнения "обуйте" человечка в башмаки, для чего постройте параллелепипед, масштабируя куб.

Итак, с помощью цилиндров и кубиков мы можем получить занятные построения, но наверняка трудно удовлетвориться только такими фигурами. Вы уже видели в одном из предыдущих примеров модель чайника и справедливо полагаете, что она создана с использованием редактора, а опорные точки треугольников извлечены мною с помощью каких-то дополнительных средств. Конечно, для масштабных проектов требуются подобные вспомогательные средства, облегчающие процесс разработки будущих элементов сцены. Большинство трехмерных редакторов и программ моделирования объектов позволяют записывать в открытом формате или применять собственные форматы с помощью встраиваемых модулей. Так, к примеру, вы можете использовать распространенный DXF-формат, поддерживаемый большинством трехмерных редакторов, а из файла такого формата легко извлекаются вершины треугольников, образующих модель. В каталоге Ех06 располагается проект, с помощью которого я получил из файла такого формата текстовый файл, содержащий данные о нормалях и треугольниках модели чайника. При запуске приложения запрашиваются имена DXF-файла и файла-результата.

Списки, переменные типа TList, Model и Normals содержат данные о считанных вершинах и вычисленных нормалях:

// Блокировать предупреждения компилятора

//о возможно пропущенной инициализации переменных

{$WARNINGS OFF}

procedure TForml.LoadDXF (const FileName : String);

var

f : TextFile;

wrkstring : String;

group, err : Integer;

xl, x2, yl, y2, zl, z2, x3, y3, z3 : Single;

// Процедура, дополняющая список вектором procedure

AddToList (const X, Y, Z : Single);

var

pwrkVector : ^TD3DVector;

begin

New (pwrkVector);

pwrkVector^ := D3DVector (X, Y, Z) ;

Model.Add (pwrkVector);

end;

begin

AssignFile(f, FileName);

Reset(f);

// Считываем данные из DXF-файла до секции ENTITIES

repeat

ReadLn(f, wrkString);

until (wrkString = 'ENTITIES') or eof(f);

while not eof (f) do begin

ReadLn (f, group); // Нулевая группа содержит вершины треугольника

ReadLn (f, wrkString); // Идентификатор либо координата

case group of

0: begin

AddToList (хЗ, y3, z3) // Добавляем вершины в список

AddToList (х2, y2, z2)

AddToList (xl, yl, zl)

end;

10: val(wrkString, xl, err)

20: val(wrkString, yl, err)

30: val(wrkString, zl, err)

11: val(wrkString, x2, err)

21: val(wrkString, y2, err)

31: val(wrkString, z2, err)

12: val(wrkString, x3, err)

22: val(wrkString, y3, err)

32: val(wrkString, z3, err)

end;

end;

CloseFile(f);

end;

{$WARNINGS ON}

// Процедура вычисления нормалей к треугольникам списка

Model procedure TForml.CalcNormals;

var

i : Integer;

wrki, vxl, vyl, vzl, vx2, vy2, vz2 : Single;

nx, ny, nz : Single;

wrkVector : TD3DVector;

pwrkVector : ^TDSDVector;

wrkVectorl, wrkVector2, wrkVectorS : TD3DVector;

pwrkVectorl, pwrkVector2, pwrkVectorS : ATD3DVector;

begin

for i := 0 to Model.Count div 3 - 1 do begin pwrkVectorl := Model [i * 3 + 1];

wrkVectorl := pwrkVectorl^; pwrkVector2 := Model [i * 3];

wrkVector2 := pwrkVector2^-

pwrkVector3 := Model [i * 3 + 2];

wrkVectorS := pwrkVector3^;

// Приращения по координатам

vxl = wrkVectorl.X - wrkVector2.X;

vyl = wrkVectorl.Y - wrkVector2.Y;

vzl = wrkVectorl.Z - wrkVector2.Z;

vx2 = wrkVector2.X - wrkVectorS.X;

vy2 = wrkVector2.Y - wrkVectorS.Y;

vz2 = wrkVector2.Z - wrkVectorS.Z;

// Вектор, перпендикулярный центру треугольника

nx := vyl * vz2 - vzl * vy2;

ny := vzl * vx2 - vxl * vz2;

nz := vxl * vy2 - vyl * vx2;

// Получаем вектор единичной длины

wrki := sqrt (nx * nx + ny * ny + nz * nz);

if wrki = 0 then wrki := 1; // Для предотвращения деления на ноль

wrkVector.X := nx / wrki;

wrkVector.Y := ny / wrki;

wrkVector.Z := nz / wrki;

New (pwrkVector);

pwrkVector^ := wrkVector;

Normals.Add (pwrkVector);

end;

end;

procedure TForml.FormCreate(Sender: TObject);

var

i : Integer; t : TextFile;

p : ATD3DVector;

n : "TDSDVector;

begin

if OpenDialogl.Execute then begin

if SaveDialogl.Execute then begin

Model := TList.Create;

Normals := TList.Create;

LoadDxf (OpenDialogl.FileName);

CalcNormals;

Caption := 'Треугольников - ' + IntToStr(Normals.Count);

AssignFile (t, SaveDialogl.FileName);

Rewrite (t);

// Запись в текстовый файл результатов

for i := 0 to Normals.Count - 1 do begin

n := Normals.Items [i];

// Первым выводится вектор нормали к треугольнику

WriteLn (t, n.X);

WriteLn (t, n.Y);

WriteLn (t, n.Z);

// Координаты вершин треугольников

р := Model.Items [i * 3};

WriteLn (t, p.X)

WriteLn (t, p.Y)

WriteLn (t, p.Z)

p := Model.Items [i * 3 + I];

WriteLn (t, p.X)

WriteLn (t, p.Y)

WriteLn (t, p.Z)

p := Model.Items [i * 3 + 2];

WriteLn (t, p.X)

WriteLn (t, p.Y)

WriteLn (t, p.Z)

end;

CloseFile (t);

Model. Free ;

Normals.Free ;

end;

end;

end;

В заголовке окна выводится количество считанных треугольников, ведь эта информация потребуется для дальнейшего кодирования. Результирующий файл не обязательно должен быть текстовым, вы можете закодировать данные. Также с помощью небольших манипуляций вы можете масштабировать модель, чтобы потом, при ее воспроизведении, не тратить на это драгоценное время.

В Internet существует масса ресурсов, содержащих свободно распространяемые модели. Например, на сайте http://www.3dcafe.com находятся сотни DXF-файлов моделей самой разнообразной тематики, и некоторыми из этих моделей я воспользовался при подготовке примеров настоящей книги. Если же нужная вам модель записана в другом формате, вы можете воспользоваться импортирующей программой.

Таких программ существует множество, я могу порекомендовать 3D Exploration, разработанную компанией X Dimension Software. Эта программа поддерживает огромный набор форматов и поэтому заслуживает вашего внимания.

С любезного разрешения авторов программы, я поместил на компакт-диск, прилагаемый к книге, демонстрационную версию продукта, которую скачал с сайта http://www.xdsoft.com/explorer.

Должен предупредить все ваши возможные вопросы о проблемах с конкретными DXF-файлами. Прежде всего, редактор или импортирующая программа, в которых создан файл, должны уметь разбивать поверхность модели на отдельные треугольники (программа, которую я вам рекомендовал, делает это успешно). В таких файлах самая громоздкая секция следует после фразы ENTITIES, за которой обязан идти большой массив данных, а не короткие фразы.

Вершины треугольников должны перечисляться либо по часовой стрелке, либо против нее. Если по полученному текстовому файлу построить модель у вас не выходит, попробуйте начать разрешение вопросов с того, что отключите отсечение. Если вы уверены, что вершины всех треугольников перечисляются в одинаковом порядке, а вместо модели выводится черный контур, то проблема состоит в вычислении нормали. Обратите внимание, что в коде этого примера при вычислении нормали я поменял порядок перечисления вершин, подобрав такую последовательность, при которой нормали перпендикулярны треугольникам. Поскольку вершин только три, вы не потеряете много времени на поиски подходящего для конкретного DXF-файла порядка. И последнее, что, возможно, вам придется сделать, если вы получаете только черную тень модели, - это поменять направление нормали на противоположное:

wrkVector.X := - nx / wrki;

wrkVector.Y := - ny / wrki;

wrkVector.Z := - nz / wrki;

Мне пришлось столкнуться с тем, что многие корреспонденты обращаются с возникающими проблемами при обработке DXF-файлов, поэтому должен четко ограничить круг действительно серьезных проблем лишь двумя: либо файл не содержит разбиение модели по треугольникам, либо вершины треугольников перечисляются в различном порядке. Во всех остальных случаях решение получить нетрудно.

Достоинствами использования DXF-файлов является то, что это открытый формат, и поддерживается он практически всеми моделирующими программами. Недостатки таковы:

* модель строится по отдельным, независимым треугольникам, что приводит к избыточности данных; это текстовый формат, поэтому для больших моделей получаются файлы гигантских размеров.

Однако в наших примерах эти файлы нужны только при подготовке кода, непосредственно при работе приложения они не применяются, и нет необходимости распространять их вместе с приложением. Наши примеры загружают данные модели из текстового файла. Полученные текстовые файлы, конечно, тоже имеют большие размеры, но помните, что вы не обязаны использовать именно текстовые файлы. Записывайте данные в виде вещественных значений, и объем файла сразу же значительно уменьшится.

А теперь перейдем к следующему примеру, проекту каталога Ех07 - несложной заготовке увлекательной игры. Вам остается только развить программу, чтобы получить законченное произведение, со стрельбой и коварными противниками, а пока что сюжет игры совсем прост: космический корабль мчится в пространстве, наполненном сферами (рис. 9.8).

Уже сейчас пример во многом напоминает профессиональный продукт: существует полноэкранный режим. Для управления положением космического корабля используется библиотека Directlnput.

Модели сферы и космического корабля загружаются из текстовых файлов, их я получил с помощью изученных утилит.

Поскольку операции с матрицами осуществляются центральным процессором, а именно нашим приложением, оптимизации их выполнения необходимо уделять максимум внимания. Для каждой движущейся сферы запоминаем текущую матрицу трансформаций, чтобы не тратить время на ее инициализацию при очередном обновлении кадра:

type

TSPHERE = packed record // Запись, относящаяся к отдельной сфере

Z : Single; // Текущая координата по оси Z

Radius : Single; // Радиус

MaterialSphere : TD3DMaterial8; // Индивидуальный материал

matSphere : TDSDMatrix; // Текущая матрица трансформаций сферы

end;

const

NumSpheres = 60; // Количество сфер

var

Spheres : Array [0..NumSpheres - 1] of TSPHERE; // Массив сфер

MaterialXWing : TD3DMaterial8; // Материал космического корабля

matXWing : TD3DMatrix; // Матрица трансформаций корабля

Заполняются целиком матрицы трансформаций сфер и корабля один раз, при инициализации:

procedure TfrmD3D.FormCreate(Sender: TObject);

var

hRet : HRESULT;

raatView, matProj : TDSDMatrix;

i : Integer; matWrk : TD3DMatrix;

begin

ShowCursor (False);

hRet := OnCreateDevice; // Инициализация библиотеки

DirectInput if Failed (hRet) then ErrorOut ('InitDirectlnput', hRet);

hRet := InitDSD;

if Failed (hRet) then ErrorOut ('InitDSD1, hRet);

hRet := InitVB;

if Failed (hRet) then ErrorOut ('InitVertex', hRet);

SetupLights;

// Инициализация массива сфер

for i := 0 to NumSpheres - 1 do with Spheres [i] do begin

// Положение по оси Z, расстояние до космического корабля

Z := random * 80 - 40;

Radius := random * 0.1+0.1; // Размер сферы

SetScaleMatrix(matSphere, Radius, Radius, Radius);

// Вспомогательная матрица трансформаций

SetTranslateMatrix (matWrk, random * 20 - 10, random * 20 - 10, Z);

// Окончательная инициализация матрицы трансформаций сферы

matSphere := MatrixMul (matSphere, matWrk);

// Инициализация материала сферы

MaterialSphere := InitMaterial(random * 0.5+0.5, random * 0.5+0.5,

random * 0.5 + 0.5, 0) ;

end;

// Космический корабль - золотистого цвета MaterialXWing := InitMaterial(1.О, 1.0, 0.0, 0); // Поворот модели по оси X SetRotateXMatrix(matXWing, -Pi /2);

// Видовая матрица и матрица проекций устанавливается один раз

SetViewMatrixfmatView, D3DVector(0, 0, -5), D3DVector(0, О, О), D3DVector(0, I, 0));

FD3DDevice.SetTransform(D3DTS_VIEW, matview);

SetProjectionMatrixdnatProj, 1, 1, 1, 100);

FD3DDevice.SetTransform(D3DTS_PROJECTION, matProj);

end;

При движении сферы в пространстве и при генерации нового ее положения не обращаемся к операциям перемножения матриц, а изменяем значение только элементов четвертой строки матрицы трансформации сферы:

procedure TfrmD3D.DrawScene;

var

i : Integer;

begin

// Рисуем космический корабль

with FDSDDevice do begin

SetMaterial(MaterialXWing); // Устанавливаем материал

// Матрица трансформаций рассчитана раньше

SetTransform(D3DTS_WORLD, matXWing);

// Модель корабля нарисована по часовой стрелке

SetRenderState(D3DRS_CULLMODE, D3DCULL_CCW);

// Вывод треугольников модели DrawPrimtive(D3DPT_TRIANGLELIST, 0, 2498);

// Сфера нарисована против часовой стрелки

SetRenderState(D3DRS_CULLMODE, D3DCULL_CW);

end;

// Вывод массива сфер

for i := 0 to NumSpheres - 1 do begin

with FDSDDevice do begin

SetMaterial(Spheres [i].MaterialSphere);

SetTransform(D3DTS_WORLD, Spheres [i].matSphere);

DrawPrimitive(D3DPT_TRIANGLELIST, 7494, 110);

end;

with Spheres [i] do begin

// Движение сферы в пространстве

Z := Z - 0.3;

// He перемножаем матрицы, меняем значение только одного элемента

Spheres [i].matSphere._43 := Z;

// Сфера улетела за пределы экрана

if Z < -20 then begin

// Генерируем новое значение координаты X сферы

matSphere._41 := random * 20 - 10;

// Генерируем новое значение координаты У сферы

matSphere._42 := random * 20-10;

Z := 50 + random (10); // Новое значение координаты Z

matSphere. 43 := Z;

// Генерируем новый материал сферы MaterialSphere := InitMaterial (random * 0.5 -t- 0.5,

random * 0.5 + 0.5, random * 0.5 + 0.5, 0);

end;

end;

end;

end;

Для максимального ускорения работы приложения из кода удалены все проверки успешности выполнения операций для каждого обновления кадра. Обратите внимание, что на сцене присутствует три источника света для освещения корабля с различных сторон.

При перемещении курсора мыши меняются значения элементов матрицы трансформаций космического корабля, при нажатых кнопках мыши происходит поворот корабля вокруг оси Y:

function TfrmDSD.ReadlmmediateData : HRESULT;

var

hRet : HRESULT;

dims2 : TDIMOUSESTATE2;

matRotateY : TD3DMatrix;

begin

ZeroMemory(@dims2, SizeOf(dims2));

hRet := DIMouse.GetDeviceState(SizeOf(TDIMOUSESTATE2), @dims2) ;

if Failed (hRet) then begin

hRet := DIMouse.Acquire;

while hRet = DIERR__INPUTLOST do

hRet := DIMouse.Acquire;

end;

// Нажата левая кнопка мыши, вращение корабля

if dims2.rgbButtons[0] = 128 then begin

SetRotateYMatrix(matRotateY, 0.1);

matXWing := MatrixMul (matXWing, matRotateY);

end;

// Правая кнопка мыши, вращение в противоположную сторону

if dims2.rgbButtons[1] = 128 then begin

SetRotateYMatrix(matRotateY, -0.1);

matXWing := MatrixMul (matXWing, matRotateY);

end;

// Движение курсора мыши, перемещение корабля по осям X и Y

matXWing._41:= matXWing._41 + 0.01 * dims2.1X;

matXWing._42 := matXWing._42 -0.01 * dims2.1Y;

Result := DI_OK;

end;

Одной из классических задач компьютерной графики является генерация ландшафтов, следующий наш пример, проект из каталога Ех08, является иллюстрацией именно на эту тему. Здесь на фоне горного ландшафта летит пассажирский лайнер, терпящий, по-видимому, катастрофу, поскольку летит с выпущенными шасси и вращается вокруг своей оси (рис. 9.9).

Формат вершин включает в себя координату, вектор нормали и цвет, порядок их следования строго определен. Тройку чисел нормали я объединил в вектор только из соображений оптимизации:

type

TCUSTOMVERTEX = packed record

X, Y, Z : Single;

normVector : TDSDVector; // Нормаль должна предшествовать цвету

Color : DWORD;

end;

const

D3DFVF_CUSTOMVERTEX = D3DFVF_XYZ or D3DFVF_NORMAL or D3DFVF_DIFFUSE;

type

LandParam = packed record // Описание опорных точек сетки ландшафта

Color : DWORD; // Цвет точки

h : Single; // Высота

VecNormal : TD3DVector; // Нормаль к вершине

end;

const

RandPoint =400; // Количество холмов и гор ландшафта

FlatLand =3; // Степень сглаживания возвышенностей

Numx = 77; // Размер ландшафта по оси X

NumZ =60; // Количество точек по оси Z

Step =0.2; // Масштабный множитель для одной площадки var

matAirplan : TD3DMatrix; // Матрица трансформаций для самолета

Land : array f1..NurnX,1..NumZ] of LandParara; // Массив ландшафта

Для генерации ландшафта произвольные вершины равномерной сетки приподнимаются на произвольную высоту. Затем, в несколько проходов, значения высот всех узлов сетки усредняются. Таким образом, вокруг пиков образуются плавные возвышенности. Для имитации горного пейзажа цвет вершин задается в зависимости от ее высоты.

При генерации ландшафта используется функция, вычисляющая нормаль к треугольнику так же, как в одном из предыдущих примеров:

procedure GenLand;

var

i, j, k : Integer;

x, z : Integer;

begin

// Генерируем вершины возвышенностей

for i := 1 to RandPoint do begin

x := random(NumX - 3) + 1;

z := random(NumZ - 3) + 1;

Land[x,z].h := random(500);

end;

// Усредняем высоты соседних точек, чтобы получить плавные холмы

for k := 1 to FlatLand do

for i:= 2 to NumX. do

for j := 2 to NumZ do

Land[i,j].h := (Land[i,j].h +

Land[(i + 1) mod NumX,j].h +

Land[i - 1, j].h +

Land[i, (j + 1) mod NumZ].h +

Land[i, j - 1].h) / 5;

// Приводим данные к удобному виду, задаем цвет вершин

for i := 1 to NumX do

for j := 1 to NumZ do

with Land[i,j] do begin

h := h / 100; if h > 0.85 then h := 0.85;

if h > 0.4 // Высокие вершины окрашиваем белым цветом

then Land[i,j].Color := $00FFFFFF else

if h > 0.2 // Точки чуть ниже - коричневым

then Land[i,j].Color := $00804000 else

if h > 0.1 // Вершины еще ниже - желтые

then Land[i,j].Color := $00FFFF00

// Точки на равнине - зеленые

else Land[i,j].Color := $0000FF00;

end;

// Рассчитываем нормали к вершинам

for i := 1 to NumX - 1 do

for j := 1 to NumZ do

CalcNormals (D3DVector (i * Step, Landfi, j - 1].h, (j - 1) * Step),

D3DVector (i * Step, Land[i, j].h, j * Step),

DSDVector ((i + 1) * Step, Landfi + 1, j - l].h,

(j - 1) * Step), Land[i, j].VecNormal);

end;

Данные модели считываются из текстового файла. В буфере вершин первые четыре вершины отводятся для построения отдельного квадрата ландшафта:

function TfrmDSD.InitVB : HRESULT;

var

Vertices : ^TCustomVertex;

hRet : HRESULT;

t : TextFile;

wrkVec : TD3DVector;

begin

FDSDDevice.CreateVertexBuffer(20665 * SizeOf(TCustomVertex), 0,

DSD FVF_CUSTOMVERTEX,

D3DPOOL_DEFAULT, FD3DVB);

FD3DDevice.SetStreamSource(0, FD3DVB, SizeOf(TCustomVertex));

FD3DVB.Lock(0, 20665 * SizeOf(TCustomVertex), PByte(Vertices), 0);

Inc (Vertices); // Первые четыре вершины отводятся для построения

Inc (Vertices); // отдельного квадрата ландшафта

Inc (Vertices);

Inc (Vertices);

AssignFile (t, 'Boeing.txt1);

Reset (t);

while not EOF(t) do begin

Readln (t, wrkVec.X); // Считываем вектор нормали

Readln (t, wrkVec.Y);

Readln (t, wrkVec.Z);

// Считываем вершины очередного треугольника

Readln (t, Vertices.X);

Readln (t, Vertices.Y);

Readln (t, Vertices.Z); .

// Исходные данные модели масштабируются

Vertices.X := Vertices.X / 3;

Vertices.Y := Vertices.Y / 3;

Vertices.Z := Vertices.Z / 3;

Vertices.normVector := wrkVec;

Vertices.Color := $00808080; // Цвет - серебристый

Inc (Vertices);

Readln (t, Vertices.X);

Readln (t, Vertices.Y);

Readln (t, Vertices.Z);

Vertices.X := Vertices.X / 3;

Vertices.Y := Vertices.Y / 3;

Vertices.Z := Vertices.Z / 3;

Vertices.normVector := wrkVec;

Vertices.Color := $00808080;

Inc (Vertices);

Readln (t, Vertices.X);

Readln (t, Vertices.Y);

Readln (t, Vertices.Z) ;

Vertices.X := Vertices.X / 3;

Vertices.Y := Vertices.Y / 3;

Vertices.Z := Vertices.Z / 3;

Vertices.normVector := wrkVec;

Vertices.Color := $00808080;

Inc (Vertices);

end;

CloseFile (t); FD3DVB.Unlock;

Result := FD3DDevice.SetVertexShader(D3DFVF_CUSTOMVERTEX);

end;

После считывания данных модели поворачиваем ее вокруг собственных осей:

procedure TfrmD3D.FormCreate(Sender: TObject);

var

hRet : HRESULT;

matView, matProj : TD3DMatrix;

matWrkl, matWrk2 : TDSDMatrix;

begin

Randomize; // Ландшафт генерируется каждый раз по-новому

ShowCursor (False); // Устанавливаем полноэкранный режим

hRet := InitD3D;

if Failed (hRet) then ErrorOut ('InitD3D', hRet);

hRet := InitVB;

if Failed (hRet) then ErrorOut ('InitVertex', hRet);

SetupLights;

// Поворачиваем самолет

SetRotateXMatrix(matWrkl, Pi / 2);

SetRotateZMatrix(matWrk2, Pi);

SetTranslateMatrix (matAirplan, 7.0, 2.0, 5.0);

// Первоначальная матрица трансформаций для самолета

matAirplan := MatrixMul (matAirplan, MatrixMul (matWrk2, matWrkl));

GenLand; // Генерируем ландшафт пейзажа

SetViewMatrix(matView, D3DVector(16, 2.5, 5),

D3DVector(0, 0, 5), D3DVector(0, 1, 0));

FD3DDevice.SetTransform(D3DTS_VIEW, matView);

SetProjectionMatrix(matProj, 1, 1, 1, 15);

FD3DDevice.SetTransform(D3DTS_PROJECTION, matProj);

end;

Ландшафт рисуется на основе данных массива, по отдельным квадратикам:

arocedure TfrmDSD.DrawArea(const x, у : Integer);

var

Vertices : ATCustomVertex;

b egin

FD3DVB.Lock(0, 4 * SizeOf(TCustomVertex), PByte(Vertices), 0) ;

Vertices.X := x * Step;

Vertices.Y := Land[x, у - 1].h;

Vertices.Z := (y - 1) * Step;

Vertices.normVector := Land[x, у - 1].VecNormal;

Vertices.Color := Land[x, у - 1].Color;

Inc (Vertices);

Vertices.X := x * Step;

Vertices.Y := Landfx, y].h;

Vertices.Z := у * Step;

Vertices.normVector := Land[x, y].VecNormal;

Vertices.Color := Landfx, y].Color;

Inc (Vertices);

Vertices.X := (x + 1) * Step;

Vertices.Y := Landfx + 1, у - 1].h;

Vertices.Z := (y - 1) * Step;

Vertices.normVector := Land[x + 1, у - 1].VecNormal;

Vertices.Color := Land[x + 1, у - 1].Color;

Inc (Vertices);

Vertices.X := (x + 1) * Step;

Vertices.Y := Land[x +1, y].h;

Vertices.Z := у * Step;

Vertices.normVector := Land[x + 1, y].VecNormal;

Vertices.Color := Land[x + 1, y].Color;

FD3DVB.Unlock;

FD3DDevice.DrawPrimitive(D3DPT_TRIANGLESTRIP, 0, 2) ;

end;

function TfrmD3D.Render : HRESULT;

var

hRet : HRESULT;

i, j :Integer;

begin

// Экран окрашивается голубоватым цветом

FD3DDevice.Clear(0, nil, D3DCLEARJTARGET or D3DCLEAR_ZBUFFER,

$00000FFF, 1.0, 0);

FD3DDevice.BeginScene; with FD3DDevice do begin

SetRenderState(D3DRS_ZENABLE, D3DZB_TRUE);

// Треугольники ландшафта перечисляются по часовой стрелке

SetRenderState(D3DRS_CULLMODE, D3DCULL_CCW);

// Вершины ландшафта сгенерированы в мировой системе координат

SetTransform(D3DTS_WORLD, IdentityMatrix);

end;

// Выводим квадратики ландшафта

for j := 2 to NumZ - 1 do

for i := 1 to NumX - 5 do DrawArea(i,j);

with FD3DDevice do begin

// Устанавливается матрица трансформаций самолета

SetTransform(D3DTS_WORLD, matAirplan);

// Вершины модели перечисляются против часовой стрелки

SetRenderState(D3DRS_CULLMODE, D3DCULL_CW);

// Данные располагаются, начиная с четвертой вершины

DrawPrimitive(D3DPT_TRIANGLELIST, 4, 20661 div 3);

end;

FD3DDevice.EndScene;

Result := FDSDDevice.Present(nil, nil, 0, nil) ;

end;

После того, как нарисован самолет, текущей трансформацией мировой матрицы остается матрица трансформаций нашей модели, поэтому перед рисованием ландшафта задаем здесь матрицу идентичности.

При каждой перерисовке кадра ландшафт циклически сдвигается, а самолет поворачивается вокруг своей оси на небольшой угол:

procedure MoveLand; // Циклическое движение пейзажа

var

i, j : Integer;

TempLand : array [l..NumX] of LandParam; // Вспомогательный массив begin

// Запомнили строку массива ландшафта

for i := 1 to NuraX do TempLand[i] := Land[i,NumZ];

// Сдвигаем ландшафт

for j := NumZ downto 2 do

for i := 1 to NumX do Land[i,j] := Landfi,j-1]; // Круговое появление последней строки массива

for i := 1 to NumX do Land[i,l] := TempLand[i];

end;

procedure TfrmDSD.ApplicationEventslIdle(Sender: TObject;

var Done: Boolean);

var

matWrk : TD3DMatrix;

begin

if FActive then begin

Render; // Нарисовали кадр

MoveLand; // Передвинули ландшафт

SetRotateYMatrix(matWrk, 0.1); // Матрица для небольшого поворота

matAirplan := MatrixMul (matAirplan, matWrk); // Поворот самолета

end;

Done := False;

end;

Для оптимизации в коде программы я матрицу поворота вычисляю один раз.

Обратите внимание на то, что в программе используется два направленных источника света, и, самое главное, на то, что формат вершин с указанием нормали и цвета позволяет воспроизводить объекты без дополнительных ухищрений. В самом деле, в программе отсутствуют материалы, и такой способ окрашивания примитивов является самым простым и быстрым.

Однако в этом примере мы сильно перерасходуем память, ведь две тысячи треугольников модели окрашиваются одним цветом, а для каждой вершины модели мы вынуждены задавать цвет. При использовании же материала память сильно экономится, но мы не получим тогда сглаживание цветов для треугольников ландшафта.

Пример проекта каталога Ех09 подсказывает возможное решение. Здесь на фоне того же ландшафта, что и в предыдущем примере, гордо парит орел (рис. 9.10).

Вкратце суть решения можно передать следующими словами: в программе применяются два буфера вершин различных форматов, один из которых не имеет цветового компонента:

type

TCUSTOMVERTEXLand = packed record

X, Y, Z : Single;

normVector : TD3DVector;

Color : DWORD;

end;

TCUSTOMVERTEXEagle = packed record

X, Y, Z :

Single;

normVector : TD3DVector;

end;

const

D3DFVF_CUSTOMVERTEXLand = D3DFVF_XYZ or D3DFVF_NORMAL or

D3DFVFJJIFFUSE; D3DFVF CUSTOMVERTEXEagle = D3DFVF_XYZ or D3DFVF_NORMAL;

При воспроизведении переключаем потоки источников, задавая в качестве таковых буферы, содержащие вершины различных форматов. При подобном подходе существенно экономится память.

Особое внимание мы должны обратить на то, как в этом примере заполняется буфер вершин модели. Рекомендованная мною импортирующая программа в качестве одного из форматов позволяет использовать код на языке C++. Для подготовки этого примера я результирующий файл преобразовал в код на языке Pascal. Это совершенно не сложно, поскольку большая его часть представляет собой массивы данных. Только имя массива, содержащего данные вершин, пришлось изменить на Avertices, чтобы не появилось конфликтов с переменной Vertices.

Первые 13 строк такого файла необходимо удалить. Также удаляются последние строки кода, начиная со строки GLint GenSoobjectListо. В оставшемся файле убираются все символы f, предшествующие запятой и фигурной скобке. Далее все фигурные скобки заменяются на обычные.

Последнее, что необходимо сделать - изменить синтаксис описания массиюв. Например, такая строка

tatic GLint face_indicies[1200][9]

заменяется следующей:

ace_indicies : array [0..1199, 0..8] of integer

Тип GLfloat заменяется типом single, остальные типы соответствуют целому.

Толученный файл с директивой include подключается к головному модулю роекта (в секцию const), а код функции инициализации буфера становится рактически универсальным, в зависимости от модели меняется только чисо, задающее размер буфера. Впрочем, и это число можно заменить выражением, опирающемся на размер массива normals. Также, возможно, потре-уется исправить и масштабный множитель:

unction TfrmD3D.InitVBEagle : HRESULT;

var

Vertices : ~TCustomVertexEagle;

hRet : HRESULT;

i, j : Integer;

vi : Integer; // Индекс вершин треугольников

ni : Integer; // Индекс нормалей треугольников

begin

hRet := FDSDDevice.CreateVertexBuffer(10500 *

SizeOf(TCustomVertexEagle), 0, D3DFVF_CUSTOMVERTEXEagle, D3DPOOL_DEFAULT, FD3DVBEagle);

if Failed(hRet) then begin

Result := hRet;

Exit;

end;

hRet := FD3DVBEagle.Lock(0, 10500 * SizeOf(TCustomVertexEagle),

PByte(Vertices), 0) ;

if Failed(hRet) then begin

Result := hRet;

Exit;

end;

// Цикл заполнения буфера данными из массивов

for i := 0 to sizeof(face_indicies) div sizeof(face__indicies[0]) - 1 do for j := 0 to 2 do begin

vi := face_indicies[i][j]; // Индекс фасета

ni := face_indicies[i] [j+3]; // Индекс нормали фасета

// Исходные данные масштабируем, умножая на 5

Vertices.X := Avertices[vi][0] * 5;

Vertices.Y := Avertices[vi][1] * 5;

Vertices.Z := Avertices[vi][2] * 5;

Vertices.normVector.X := normals[ni] [0] ;

Vertices.normVector.Y := normals[ni][1];

Vertices.normVector.Z := normals[ni][2];

Inc(Vertices);

end;

Result := FDSDVBEagle.Unlock;

end;

При инициализации работы один раз устанавливается материал, а при воспроизведении необходимо указывать, окрашивание производится исходя из цветовой составляющей вершины, либо используется установленный материал:

with FDSDDevice do begin

SetRenderState(D3DRS_ZENABLE, D3DZB_TRUE);

SetRenderState(D3DRS_CULLMODE, D3DCULL_CCW);

// Для ландшафта цвет примитивов задается цветовой составляющей вершин

SetRenderState(D3DRS_DIFFUSEMATERIALSOURCE, D3DMCS_COLOR1);

SetTransform(D3DTS_WORLD, IdentityMatrix); // Выключаем третий источник,

// предназначенный для освещения только модели

LightEnable(2, False);

SetStreamSource(0, FD3DVBLand, SizeOf(TCustomVertexLand));

SetVertexShader(D3DFVF_CUSTOMVERTEXLand);

end;

// Вывод треугольников ландшафта

for j := 2 to NumZ - 1 do

for i := 1 to NumX - 5 do

DrawAreafi, j);

with FDSDDevice do begin

SetTransform(D3DTS_WORLD, matEagle);

LightEnable(2, True); // Включаем дополнительный источник

SetStreamSource(0, FD3DVBEagle, SizeOf(TCustomVertexEagle));

SetVertexShader(D3DFVF_CUSTOMVERTEXEagle) ;

// Окрашивание осуществляется исходя из свойств материала

SetRenderState(D3DRS_DIFFUSEMATERIALSOURCE, D3DMCS_MATERIAL);

DrawPrimitive{D3DPT_TRIANGLELIST, 0, 10500 div 3);

end;

По умолчанию для режима D3DRS_DiFFUSEMATERlALSoracE устанавливается значение D3DMCS_COLOR1. Здесь же мы восстанавливаем это значение, потерянное после воспроизведения модели орла.

Закончу главу небольшими замечаниями по поводу моделей. Конечно, совсем не обязательно, чтобы используемые вами модели были однотонными, как в моих примерах. Импортирующая программа, рекомендованная мной, позволяет записывать в DXF-файлах (или в другом формате) отдельные части моделей. Вы можете разбить модель на части, считывать данные на них по отдельности и окрашивать фрагменты в различные цвета, меняя текущий материал, или задавать нужный цвет вершин.

Если данные модели заполняются так же, как в последнем примере, в виде массивов констант, и без расчета нормалей, то массивы могут храниться в отдельных файлах внутреннего формата или загружаться из библиотек. В этом случае размер главного модуля станет меньше. Также мне необходимо уточнить, что модель строится группой несвязанных треугольников.

Что вы узнали в этой главе

Глава посвятила нас в премудрости матричных операций, что позволило нам перенести построения в пространство. Мы узнали, как с помощью несложных средств можно создавать составные объекты. Хотя примеры главы крайне просты, усердные читатели смогут легко развить их до совершенных и серьезных программ.