Книга: Размышления о думающих машинах. Тьюринг. Компьютерное исчисление
И-НЕ — ВАЖНЫЙ ВЕНТИЛЬ ДЛЯ РАЗРАБОТКИ НЕЙРОНОВ
И-НЕ — ВАЖНЫЙ ВЕНТИЛЬ ДЛЯ РАЗРАБОТКИ НЕЙРОНОВ
Одним из практических аспектов цифровой электроники и следствием булевой алгебры является тот факт, что вентили И и ИЛИ могут получиться из вентиля И-НЕ (NAND), то есть вентиля И, выход которой трансформирован вентилем НЕ. Вентиль НЕ имеет единственный вход и единственный выход и изменяет величину одного бита: если на входе О, то на выходе 1, и наоборот. Для его обозначения используется следующий символ.
| А | НЕ А |
| 0 | 1 |
| 1 | 0 |
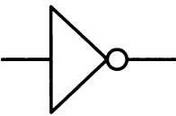
Поведение вентиля И-НЕ представлено в таблице. Рядом — символ, используемый для обозначения данного вентиля.
| А | НЕ А | А И-НЕ В |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
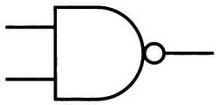
На следующей схеме показано, как соединить вентили И-НЕ между собой, чтобы получить вентили И и ИЛИ.
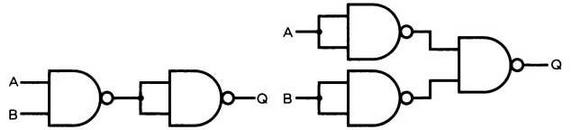
Взаимное соединение вентилей И-НЕ для получения вентиля И (слева) и вентиля ИЛИ (справа) со входами А, В и выходом Q.
В статье «Умные машины», одной из первых в мире работ по искусственному интеллекту, Алан Тьюринг использовал вентили И-НЕ для симуляции нейронных цепей, которые назвал нейронными цепями типа В.
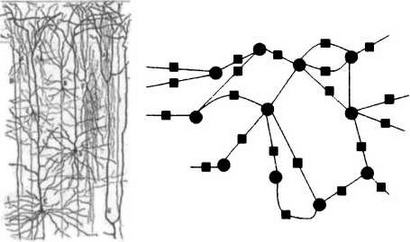
Нейронная сеть, изображенная Сантьяго Рамон-и-Кахалем (слева), и искусственная нейронная сеть (справа).
Эти волокна определяют конфигурацию нейронов: возбужденное состояние или нейтральное. В возбужденном состоянии, когда волокно Р активно, если модификатор связи получает на входе input 0 или 1, на выходе output будет возвращен тот же результат, 0 или 1 соответственно. С другой стороны, в нейтральном состоянии, когда волокно I активно, модификатор соединения будет вести себя так, что при любой величине на входе input, на выходе output результат всегда будет 1.
Кроме этих модификаторов, модель искусственного нейрона предполагала, что каждый нейрон имел два входа: ВХОД 1 и ВХОД 2 — и один ВЫХОД. Если оба входа находились в возбужденном состоянии, величина на ВЫХОДЕ получалась с применением булева оператора И-НЕ (вентиль И, выход которого соединяется с вентилем НЕ).
| ВХОД 1 | ВХОД 2 | выход |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Напротив, если ВХОД 1 находился в неактивном состоянии, величина на ВЫХОДЕ была равна обратной величине на ВХОДЕ 2, то есть 1, когда на ВХОДЕ 2 было 0 и наоборот.
| ВХОД 1 | ВХОД 2 | выход |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Если мы сравним модель искусственного нейрона Тьюринга с моделью Маккалока — Питтса, то увидим, что в последней величина на ВЫХОДЕ рассчитывается с заменой модификатора соединения на величину коэффициента w, который отражает синаптическую пластичность нейронов, то есть лучшую или худшую проходимость сигнала от одного нейрона к другому через синаптическую связь. Согласно формальной модели Маккалока — Питтса, нейрон ведет себя как калькулятор, способный вычислять сумму входных сигналов. Умножим каждый сигнал или ВХОД i на соответствующий коэффициент wi, сумму всех сигналов обозначим как ИТОГ:
ИТОГ = ?wi ВХОДi
После выполнения данной операции нейрон «решает», достаточна ли полученная информация ИТОГ для активации, или возбуждения. В самой элементарной модели нейрона величина ВЫХОДА получается с помощью ступенчатой функции:
1 ИТОГ ? U
ВЫХОД =
0 ИТОГ ? U
При этом величина порога U устанавливается предварительно. Обратим внимание, что эта величина показывает чувствительность нейрона к внешнему стимулу: нейрон более чувствителен, чем ближе к нулю величина ?, так как чем меньше порог, тем вероятнее, что ИТОГ превзойдет его величину при возбуждении нейрона. Если величина на ВЫХОДЕ равна нулю, нейрон останется в состоянии покоя, если на ВЫХОДЕ будет некоторая величина, нейрон перейдет в возбужденное состояние. При возбуждении нейрон отправляет ответ, величину 1, следующему нейрону, для которого это будет величина на ВХОДЕ. В других случаях величина 1 в комбинации с величинами на ВЫХОДЕ от других нейронов, например 1001, будет ответом нейронной сети на входящий сигнал.
- ЯВЛЯЕТСЯ ЛИ МОЗГ МАШИНОЙ ТЬЮРИНГА?
- ПОСТРОИТЬ КОМПЬЮТЕР ИЗ ИСКУССТВЕННЫХ НЕЙРОНОВ
- И-НЕ — ВАЖНЫЙ ВЕНТИЛЬ ДЛЯ РАЗРАБОТКИ НЕЙРОНОВ
- ТЕСТ ТЬЮРИНГА
- КАПЧА
- ВЕЛИКАЯ ПАРТИЯ: ГАРРИ КАСПАРОВ ПРОТИВ АЛАНА ТЬЮРИНГА
- КАК КОМПЬЮТЕР ИЗУЧАЕТ РОСТ И РАЗВИТИЕ ЖИВЫХ СУЩЕСТВ
- РАЗГОВОР С ЭЛИЗОЙ
- ИЗУЧЕНИЕ ПОДСОЛНУХОВ. НЕЗАКОНЧЕННЫЙ ОПЫТ ТЬЮРИНГА
- ТРАГИЧЕСКАЯ РАЗВЯЗКА
- 1.8. СТАДИИ И ЭТАПЫ РАЗРАБОТКИ ПРОГРАММ
- 3. Участники разработки экспертных систем
- Часть III. Шаблоны разработки через тестирование
- 1.1. Схема и основные этапы разработки новой продукции
- 5.5. ПРИМЕР РАЗРАБОТКИ ОПИСАНИЯ ПРОЦЕССА "КИПЯЧЕНИЕ ВОДЫ В ЧАЙНИКЕ"
- IBPP для разработки C++
- 7.2. Этапы разработки
- Процесс разработки программного обеспечения
- Дополнительные средства разработки .NET-приложений
- Установка библиотек разработки GNOME
- 1.2. ОБЩИЕ ПРИНЦИПЫ РАЗРАБОТКИ ПРОГРАММ
- Как язык программирования и среда разработки влияют на TDD?




