Книга: Размышления о думающих машинах. Тьюринг. Компьютерное исчисление

ПОСТРОИТЬ КОМПЬЮТЕР ИЗ ИСКУССТВЕННЫХ НЕЙРОНОВ

Один из интересных опытов, который мы можем проделать с нейронами Маккалока — Питтса, — это использование их в качестве компонентов компьютера. В таком компьютере арифметические и логические операции будут выполняться внутри микропроцессора в арифметико-логическом устройстве (АЛУ). Нейронные цепи могут выполнять операции, схожие с компьютерными, с помощью логических вентилей, например И, ИЛИ, а также другие операции, свойственные биологическим нейронам. Процедура построения логического вентиля, выполняющего операцию булевой алгебры, начинается с определения соответствующих величин для коэффициентов соединений (w_± и w₂) и порога активации (U), как показано на схеме.

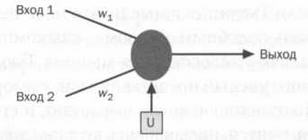
Комбинируя несколько искусственных нейронов, пошагово соединяя выходы одних со входами других, мы можем получить цепи, эмулирующие операторы И и ИЛИ. Однако можно сделать это проще, с одним нейроном Маккалока — Питтса. Эти простые опыты доказывают, что, как и думали Тьюринг, Маккалок и Питтс, нейрон является автоматом с двумя состояниями: активным, или возбужденным (1), и состоянием покоя (0), а также что нейронная цепь может выполнять функции, схожие с функциями арифметико-логического устройства (АЛУ) компьютера. Используем следующую программу на языке BASIC-256, чтобы показать, что нейрон будет вести себя как вентиль И при следующих входящих (О и 1) и исходящих сигналах.

rem Оператор И

els

wl=0.5:w2=0.5:u=0.5

input "вход 1 = ",el

input "вход 2 = ",e2

total=wl*el+w2*e2

if total <=u then

print "выход = 0"

else

print "выход = 1"

end if

С другой программой нейрон будет вести себя как вентиль ИЛИ.

rem Оператор ИЛИ

els

wl=l:w2=l:u=0.5

input "вход 1 = ",el

input "вход 2 = ",e2

total=wl*el+w2*e2

if total <=u then

print "выход = 0"

else

print "выход = 1"

end if

Итак, какой же была модель искусственного нейрона Алана Тьюринга? Представим, что нейрон — это круг, соединенный с другими кругами, символизирующими соседние нейроны. Добавим в местах соединений прямоугольник, который будет обозначать модификатор связи Тьюринга, дающий дезорганизованной машине типа В способность обучаться. Каждый модификатор связи имеет две линии, или «волокна тренировки», которые мы обозначим как Р и I.

Оглавление книги