Книга: Золотой билет

Иголка в стоге сена

Иголка в стоге сена

Предположим, мы ищем клику из трех человек среди всех 20000 жителей Королевства. По самым грубым подсчетам нужно проверить чуть больше триллиона вариантов – сущая ерунда для любого современного компьютера. Однако дальше варианты начинают размножаться с космической скоростью, перед которой компьютеры очень быстро пасуют: для клики размера четыре требуется уже 6 квадриллионов проверок, для клики размера пять – 26 квинтиллионов, а для клики размера шесть – 88 секстиллионов (т. е. 88 и 21 ноль).

Впрочем, поиск «иголки в стоге сена» не всегда превращается в такую катастрофу. Группа жителей Королевства считается очень приятной, если для любой пары друзей хотя бы один из них в эту группу входит.

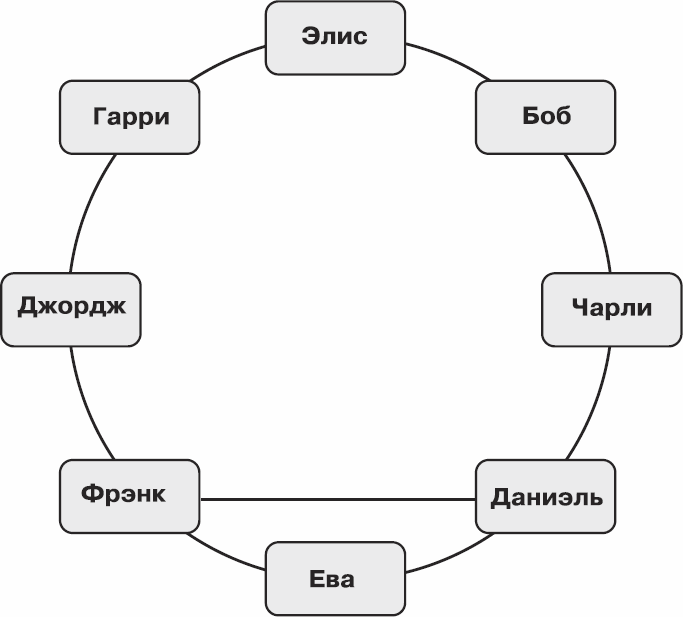
Рис. 6.8. Дружеские связи

На представленной выше диаграмме Боб, Даниэль, Фрэнк и Гарри образуют очень приятную группу, поскольку все дружеские связи (линии на схеме) завязаны на них.

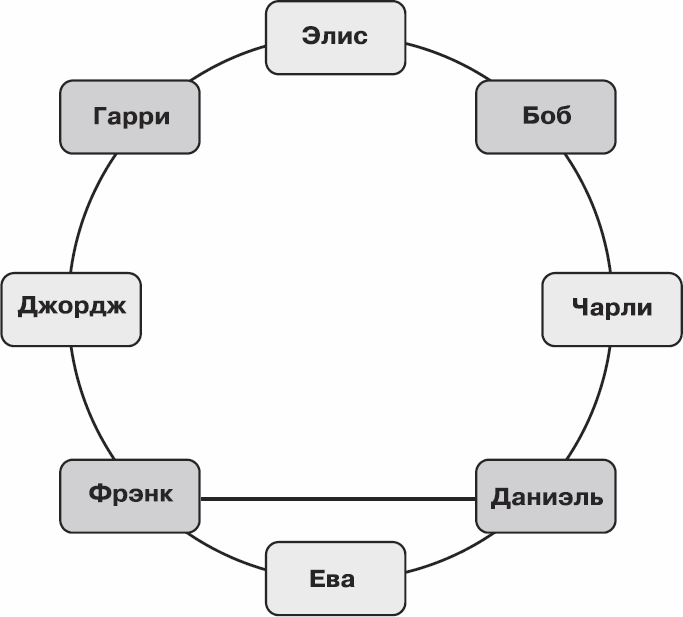
Рис. 6.9. Очень приятная группа размера четыре

А вот очень приятную группу размера три составить уже не получится. Например, если взять Элис, Чарли и Фрэнка – потеряются дружеские связи Ева – Даниэль и Джордж – Гарри.

Задача поиска очень приятной группы, более известная под официальным названием «задача о вершинном покрытии», принадлежит к «старой гвардии» и упоминается еще в списке NP-полных задач Карпа.

Давайте взглянем на дружеские связи Фрэнка. Если Фрэнк не является членом очень приятной группы, то тогда в нее должны входить Джордж, Даниэль и Ева, поскольку все они с Фрэнком друзья. Каждая очень приятная группа обязательно содержит либо Фрэнка, либо всех его друзей – даже если их не три, а целых сто.

При помощи подобных хитростей можно избежать полного перебора всех потенциальных вариантов при поиске небольших очень приятных групп. Для группы размера пять понадобится около 100000 проверок, для группы размера 10–200000 проверок, а для группы размера 30–601000 проверок; любой ноутбук справится с такой задачей за считаные доли секунды. Поиск очень приятной группы размера 113 потребует проверки триллиона вариантов и будет длиться не дольше, чем поиск клики из каких-то несчастных трех человек.

Рис. 6.10. Не очень приятная группа размера 3

Стоп. Выходит, очень приятные группы искать не так уж сложно? Но разве Карп не доказал, что поиск очень приятной группы минимального размера (т. е. минимального вершинного покрытия) – задача NP-полная? Дело в том, что у жителей Королевства друзей обычно очень много. Маловероятно, что все дружеские связи завязаны лишь на 113 жителях. А как только мы замахнемся на группы побольше, число вариантов тут же резко возрастет.

Например, для группы размера 150 потребуется уже 1,5 квадриллиона проверок, для группы размера 200 – более секстиллиона, а для группы размера 500 – примерно 38 сексдециллионов (т. е. 38 и 51 ноль). Поиск очень приятной группы минимального размера – задача практически неразрешимая. А вот если нам просто нужно убедиться, что в Королевстве не существует очень приятной группы размера сто, мы получим ответ за разумное время.

Оглавление книги