Книга: Золотой билет

Передай скипетр

Передай скипетр

Иногда достаточно внести лишь одно незначительное изменение, чтобы задача, решение которой находится очень легко, стала прямо-таки неприступной, и сейчас мы с вами в этом убедимся.

Дети в Королевстве любят играть в игру под названием «Передай скипетр», в которой участники по очереди передают друг другу небольшую палку. Передачей считается тот момент, когда палку держат двое – передающий и принимающий.

Правила игры:

1. Палку можно передавать только друзьям.

2. Между любыми двумя друзьями палка должна переместиться ровно один раз.

Пусть в игре участвуют пятеро детей. Одно из возможных решений таково: начинают с Барбары, она передает палку Эрику, Эрик – Алексу, Алекс – Кэти, Кэти – снова Эрику, а Эрик – Дэвиду.

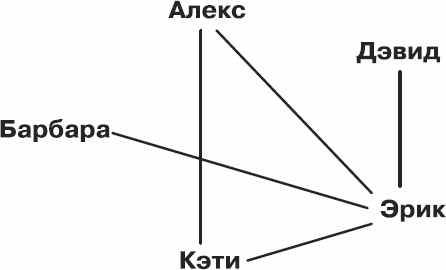
Рис. 3.6. Дети

Дети, которые играют в «Передай скипетр» часто, вскоре понимают: решение существует, когда нечетное число друзей среди игроков имеется не более чем у двух участников. В данном случае таких участников у нас ровно два – это Дэвид и Барбара, у каждого из которых среди играющих есть только один друг. У остальных детей количество друзей четно: у Алекса и Кэти – по два, у Эрика – четыре. Вы спросите, причем тут четность? А вот причем: чтобы передать кому-то палку, нужно сначала получить ее, поэтому каждый игрок, кроме первого и последнего, обязательно участвует в четном количестве передач.

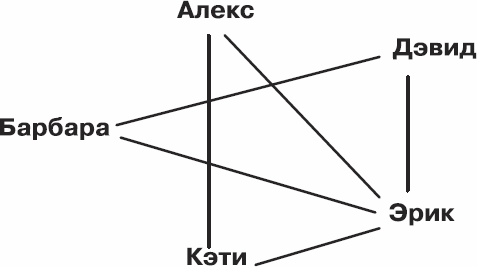
Рис. 3.7. Дети: число друзей у всех четно

Когда у всех участников число друзей четно, в случае успешного исхода палка возвращается к тому, с кого начали.

В данной ситуации решение может быть таким: начинают с Алекса, он передает палку Эрику, Эрик – Дэвиду, Дэвид – Барбаре, Барбара – снова Эрику, Эрик – Кэти, а Кэти – Алексу.

Прообразом игры «Передай скипетр» послужила одна очень известная головоломка XVIII века. В прусском городе Кёнигсберге (а ныне российском Калининграде) через реку Прегель и ее рукава было перекинуто семь мостов (см. карту на рис. 3.8).

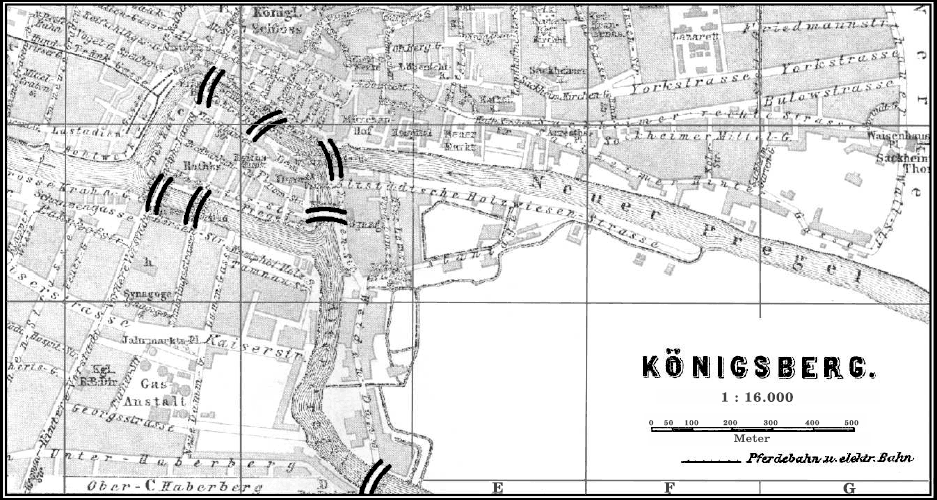
Рис. 3.8. Старинная карта мостов Кёнигсберга

Жителям долгое время не давал покоя вопрос: можно ли посетить все районы города, проходя по каждому мосту ровно один раз? В 1735 году знаменитый математик Леонард Эйлер придумал, как изобразить задачу в виде схемы (см. рис. 3.9).

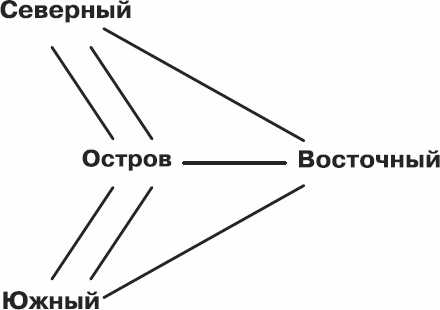
Рис. 3.9. Схема Эйлера

Очень похоже на игру со скипетром, и критерий существования решения здесь тот же; единственное отличие заключается в том, что узами дружбы связаны уже не дети, а районы города – Северный, Восточный, Южный и Остров. Эйлер доказал, что пройти по каждому мосту ровно один раз невозможно, поскольку во всех районах города количество мостов нечетно.

Так и выяснилось, что задача о семи мостах не имеет решения. В память об этом в игре со скипетром любой подходящий путь (а их бывает несколько) называется эйлеровым. Эйлеров путь можно искать по-разному, в том числе и простым перебором, однако при увеличении количества участников число вариантов заметно возрастает. Дети в Королевстве первым делом пересчитывают игроков с нечетным числом друзей, чтобы понять, существует ли вообще решение; если оно существует, то найти искомый путь уже не составляет особого труда. Поиск эйлерова пути – еще один пример задачи из класса P, т. е. задачи, для которой существует эффективный алгоритм.

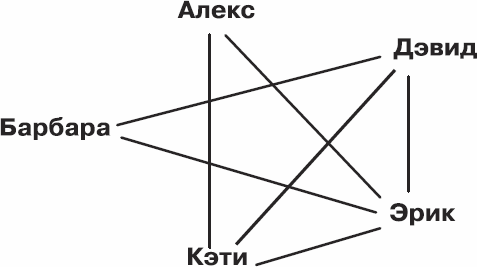
Рис. 3.10. Передай скипетр – 2: решение есть

Постепенно дети подрастают. Играть становится все легче и легче; в конце концов «Передай скипетр» надоедает им, и тогда они начинают играть в ее вариацию, которую кто-то, не мудрствуя лукаво, окрестил «Передай скипетр – 2». Правила игры следующие:

1. Палку можно передавать только друзьям.

2. Все игроки, кроме первого, получают палку ровно один раз; в конце палка возвращается к первому игроку.

Для представленной ниже схемы дружеских связей решение может быть таким: Дэвид передает скипетр Барбаре, Барбара – Эрику, Эрик – Алексу, Алекс – Кэти, а Кэти возвращает его Дэвиду.

А вот для следующей схемы решения, как выяснилось, не существует.

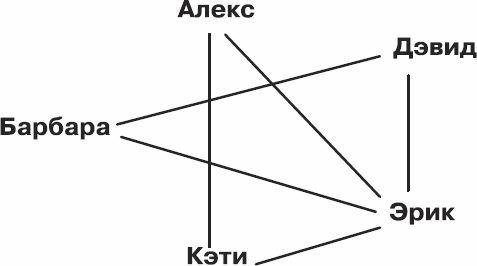
Рис. 3.11. Передай скипетр – 2: решения нет

Новые правила выглядят проще. Поначалу детям даже кажется, что вторая игра легче, чем первая, однако при увеличении числа участников играть в нее становится намного сложнее. В 1857 году математик Уильям Роуэн Гамильтон изобрел головоломку «Икосиан», или «Путешествие по додекаэдру», в которой нужно было выполнить обход вершин правильного двенадцатигранника, или додекаэдра.

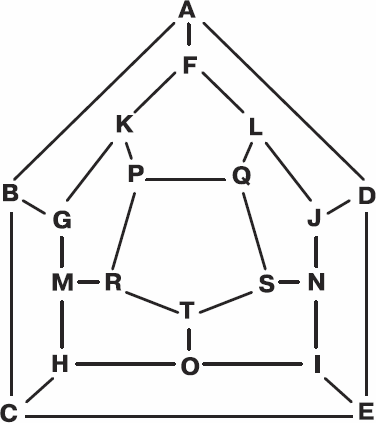
Рис. 3.12. «Путешествие по додекаэдру»

Эта головоломка – частный случай второй игры со скипетром. Представьте, что вершины додекаэдра соответствуют жителям Королевства, а ребра соединяют друзей, – и получите самую настоящую схему дружеских связей. Сумеете сами обойти додекаэдр и решить вторую игру со скипетром? Ответ вас ждет в конце главы.

Любой путь, удовлетворяющий условиям игры, в честь создателя головоломки называется гамильтоновым циклом.

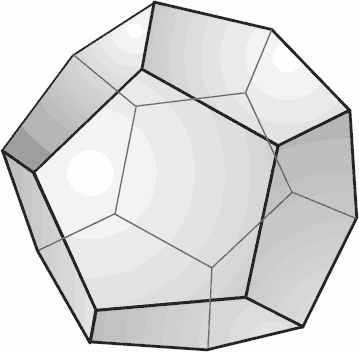
Рис. 3.13. Додекаэдр

Оглавление книги