Книга: Фундаментальные алгоритмы и структуры данных в Delphi

Детерминированные и недетерминированные конечные автоматы

Детерминированные и недетерминированные конечные автоматы

Теперь, когда мы рассмотрели несколько достаточно сложных конечных автоматов и ближе познакомились с ними, следует ознакомиться с рядом новых терминов. Первый из них - автомат (automaton или, в просторечии, automata). Это всего лишь еще одно название машины состояний, которое используется исключительно в учебных курсах и учебниках по компьютерным наукам. Конечный автомат (он же и конечная машина состояний) - это всего лишь машина состояний, количество состояний которой не бесконечно. Оба приведенные ранее примера представляли конечные автоматы: в первом имелось три состояния, во втором -пять.

И еще один новый термин - детерминированный (deterministic). Взгляните на конечный автомат, представленный на рис. 10.2. Независимо от текущего состояния и от того, каким будет следующий символ, точно известно, в какое состояние должен быть выполнен переход. Все переходы полностью определены. Этот конечный автомат является детерминированным. В процессе его работы не требуется делать какие-либо предположения или осуществлять выбор. Например, если бы двойная кавычка была получена во время нахождения в состоянии FieldStart, потребовалось бы выполнить переход в состояние ScanQuoted.

Рисунки 10.1 и 10.2 служат примерами детерминированных конечных машин состояний (deterministic finite state machines - DFSM), или детерминированных конечных автоматов (deterministic finite automata - DFA). Противоположными им являются конечные автоматы, в ряде состояниях которых требуется осуществлять какой-либо выбор. При использовании конечного автомата этого типа приходится решать, нужно ли для данного конкретного символа выполнять переход в состояние X или в состояние Y. Как можно догадаться, реализация конечного автомата такого вида требует несколько более сложного кода. Не удивительно, что эти конечные автоматы называются недетерминированными конечными машинами состояний (non-deterministic finite state machines - NDFSM), или недетерминированными конечными автоматами (deterministic finite automata - NFA).

Теперь рассмотрим NFA-автомат. На рис. 10.3 показан NFA-автомат, который может преобразовывать строку, содержащую число в десятичном формате, в двоичное значение. При взгляде на этот рисунок у читателей может возникнуть вопрос, что представляют собой переходы, обозначенные странным символом е. Это -бесплатные, или свободные переходы, которые можно выполнить без использования текущего символа или лексемы. Так, например, от начала лексемы A к следующей лексеме В можно перейти, используя знак "+", знак "-" или просто выполнив это переход (бесплатный переход). Эти свободные переходы - отличительная особенность недетерминированных конечных автоматов.

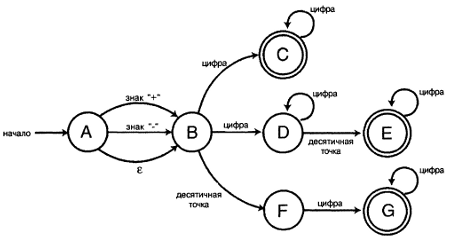
Рисунок 10.3. NFA-автомат для проверки, является ли строка числом

Воспользуемся этим рисунком для проверки таких строк, как "1", "1.23", "+.7", "-12". Как видите, верхняя ветвь служит для обработки целочисленных значений (не содержащих десятичной точки). Средняя ветвь выполняет обработку строк, которые состоят, по меньшей мере, из одной цифры, предшествующей десятичной точке, но которые могут и не иметь цифр, следующих за точкой. Нижняя ветвь предназначена для обработки строк, которые могут не содержать ни одной цифры перед десятичной точкой, но обязательно должны содержать хотя бы одну цифру после нее. Если немного подумать, становится понятно, что этот конечный автомат не сможет воспринимать самостоятельно вводимую десятичную точку.

Однако одна проблема остается нерешенной: хотя конечный автомат воспримет строку "1.2", как он "узнает", что нужно выполнять среднюю ветвь? Более того, может возникать более принципиальный вопрос: зачем вообще связываться с NFA-автоматом? Весь алгоритм кажется слишком сложным. Поэтому, почему бы не ограничиться применением DFA-автомата?

В действительности на второй вопрос проще ответить, чем на первый. NFA -естественные конечные автоматы для вычисления регулярных выражений. Разобравшись в использовании NFA-автоматов, мы проходим более половины пути к конечной цели этой главы - к возможности сопоставления строки с регулярным выражением.

Вернемся к первому вопросу: откуда NFA-автомат знает, что для строки "1.2" необходимо выполнять среднюю ветвь алгоритма? Естественно, автомат этого не знает. Существует несколько способов обработки строки с помощью подобного конечного автомата. И простейшим для описания является алгоритм проб и ошибок. В качестве вспомогательного мы используем еще один алгоритм - алгоритм с отходом (backtracking algorithm).

Обратите внимание, что нас интересует определение только одного пути конечного автомата, воспринимающего строку. Могут существовать и другие, но перечисление их всех интереса для нас не представляет.

Посмотрим, как работает этот алгоритм, проследив, что происходит при попытке ввода строки "12.34".

Работа алгоритма начинается с состояния A. Первой лексемой является "1". Мы не можем выполнить ни переход "+" в состояние В, ни переход "-". Поэтому мы выполняем свободный переход (связь е). В результате автомат оказывается в состоянии В с той же лексемой "1". Теперь у нас имеются две возможности: выполнить переход в состояние С или в состояние D, поглощая при этом лексему. Выберем первую возможность. Прежде чем выполнить переход, отметим, что именно мы собираемся сделать, чтобы в случае неудачи не повторять ошибку. Итак, мы выполняем переход в состояние С, поглощая при этом лексему. Мы получаем вторую лексему, "2". Пока все достаточно просто. Автомат остается в том же состоянии и использует лексему.

Мы получаем следующую лексему ".". Теперь возможные переходы вообще отсутствуют. Мы оказались в тупике. Возможные переходы отсутствуют, но имеется лексема, которую нужно обработать. Именно здесь выступает на сцену алгоритм с отходом. Просмотрев свои заметки, мы замечаем, что в состоянии В был сделан выбор, при котором была предпринята попытка использования лексемы "1". Вероятно, этот выбор был ошибочным, поэтому мы осуществляем отход, чтобы найти правильное решение. Мы сбрасываем конечный автомат обратно в состояние В, а значение входной строки - в значение лексемы "1". Поскольку выбор первой возможности привел к проблеме, мы проверяем вторую возможность: переход в состояние D. Мы выполняем этот переход, поглощая лексему "1". Следующая лексема - "2". Мы используем ее и остаемся в состоянии D. Следующая лексема - ".": она обусловливает переход в состояние Е, которое фактически поглощает следующие две цифры. Входная строка исчерпана и NFA-автомат находится в конечном состоянии. Поэтому можно сказать, что NFA-автомат воспринимает строку "12.34".

При преобразовании этого конечного автомата в код потребуется решить несколько проблем.

Во-первых, мы больше не располагаем простым циклом For для циклической обработки символов в строке. В случае применения детерминированного автомата каждый считываемый из входной строки символ вызывал переход (даже если это переход в то же самое состояние) и отсутствовала какая-либо возможность отхода или возврата к уже посещенному символу. В случае применения недетерминированного конечного автомата мы заменяем цикл For циклом While и при необходимости обеспечиваем увеличение переменной индекса строки.

Во-вторых, в некоторых состояниях мы не можем использовать применительно к входному символу простой оператор Case или If. Нам приходится иметь дело с множеством "вариантов перехода". Некоторые из них будут немедленно отбрасываться, поскольку текущий символ не соответствует условию перехода. Другие будут приняты, причем некоторые из них будут отброшены на более позднем этапе, а какой-то вариант будет использован. А пока просто пронумеруем возможные переходы и поочередно их выполним. Для этого будем использовать целочисленную переменную.

Теперь нужно рассмотреть последний фрагмент кода: реализацию собственно алгоритма с отходом. При каждом выборе допустимого перехода (сравните его с отбрасыванием перехода из-за того, что текущий символ не соответствует условиям перехода) необходимо сохранить информацию о конкретном выполненном переходе. Тогда, при необходимости выполнить отход к тому же состоянию с тем же самым входным символом, можно легко выбрать следующий переход и проверить его. Конечно, выбор вариантов переходов может требоваться в любом состоянии. Поэтому нужно записать их все, чтобы их можно было выполнить в обратном порядке. Отход выполняется в состояние, предшествовавшее последнему сделанному выбору. Иначе говоря, следует воспользоваться структурой типа "последним вошел, первым вышел", т.е. стеком. Применим один из стеков, которые были реализованы в главе 3.

Что же нужно сохранять в стеке? Разумеется, в нем необходимо сохранять состояние, в котором был сделан выбор, номер выполненного перехода (чтобы для проверки можно было выбрать следующий переход) и, наконец, индекс символа, для которого был осуществлен выбор. Используя эти три информационных элемента, можно легко вернуть конечный автомат к предшествующему состоянию, чтобы можно было выбрать следующий, и, возможно, более удачный вариант перехода.

Код реализации NFA-автомата для анализа десятичных чисел приведен в листинге 10.3. Этот конечный автомат будет поглощать строку в момент, когда строка исчерпана, а автомат находится в конечном состоянии. Автомат не примет строку, если строка исчерпана, а состояние отличается от конечного, или если в данном состоянии текущий символ не удовлетворяет условиям перехода. Во второй ситуации должно выполняться также следующее условие: стек отхода должен быть пуст.

Листинг 10.3. Проверка того, что строка является числом, с помощью NFA-автомата

type

TnfaState = ( StartScanning, {состояние A на рисунке}

ScannedSign, {состояние B на рисунке}

ScanInteger, {состояние C на рисунке}

ScanLeadDigits, {состояние D на рисунке}

ScannedDecPoint, {состояние E на рисунке}

ScanLeadDecPoint, {состояние F на рисунке}

ScanDecimalDigits); {состояние G на рисунке}

PnfaChoice = ^TnfaChoice;

Tnf aChoice = packed record

chInx : integer;

chMove : integer;

chState : TnfaState;

end;

procedure DisposeChoice(aData : pointer);

far;

begin

if (aData <> nil) then

Dispose(PnfaChoice(aData));

end;

procedure PushChoice( aStack : TtdStack;

aInx : integer;

aMove : integer;

aState : TnfaState);

var

Choice : PnfaChoice;

begin

New(Choice);

Choice^.chInx := aInx;

Choice^.chMove := aMove;

Choice^.chState := aState;

aStack.Push(Choice);

end;

procedure PopChoice(aStack : TtdStack;

var aInx : integer;

var aMove : integer;

var aState : TnfaState);

var

Choice : PnfaChoice;

begin

Choice := PnfaChoice(aStack.Pop);

aInx := Choice^.chInx;

aMove := Choice^.chMove;

aState := Choice^.chState;

Dispose(Choice);

end;

function IsValidNumberNFA(const S : string): boolean;

var

StrInx: integer;

State : TnfaState;

Ch : AnsiChar;

Move : integer;

ChoiceStack : TtdStack;

begin

{предположим, что число является недопустимым}

Result :- false;

{инициализировать стек вариантов}

ChoiceStack := TtdStack.Create(DisposeChoice);

try

{подготовиться к сканированию}

Move := 0;

StrInx := Instate := StartScanning;

{считывание всех символов строки}

while StrInx <= length(S) do

begin

{извлечь текущий символ}

Ch := S[StrInx];

{обработать в зависимости от состояния}

case State of

StartScanning : begin

case Move of

0 : {переход к ScannedSign по ветви +}

begin

if (Ch = '+') then begin

PushChoice(ChoiceStack, StrInx, Move, State);

State := ScannedSign;

Move := 0;

inc(StrInx);

end else

inc(Move);

end;

1 : {переход к ScannedSign по ветви -}

begin

if (Ch = '-') then begin

PushChoice(ChoiceStack, StrInx, Move, State);

State := ScannedSign;

Move := 0;

inc(StrInx);

end else

inc(Move);

end;

2 : {бесплатный переход к ScannedSign}

begin

PushChoice(ChoiceStack, StrInx, Move, State);

State ScannedSign;

Move := 0;

end;

else

{для этого состояния допустимые переходы отсутствуют}

Move := -1;

end;

end;

ScannedSign : begin

case Move of

0 : {переход x Scanlnteger с использованием цифры}

begin

if TDIsDigit(Ch) then begin

PushChoice(ChoiceStack, StrInx, Move, State);

State := Scanlnteger;

Move := 0;

inc(StrInx);

end else

inc(Move);

end;

1 : {переход к ScanLeadDigits с использованием цифры}

begin

if TDIsDigit (Ch) then begin

PushChoice(ChoiceStack, StrInx, Move, State);

State := ScanLeadDigits;

Move := 0;

inc(StrInx);

end else

inc(Move);

end;

2 : {переход к ScanLeadDigits с использованием десятичного разделителя}

begin

if (Ch = DecimalSeparator) then begin

PushChoice(ChoiceStack, StrInx, Move, State);

State := ScanLeadDecPoint;

Move := 0;

inc(StrInx);

end else

inc(Move);

end;

else

{для этого состояния допустимые переходы отсутствуют}

Move := -1;

end;

end;

Scanlnteger : begin

case Move of

0 : {сохранить данное состояние для текущей цифры}

begin

if TDIsDigit(Ch) then

inc(StrInx) else inc(Move);

end;

else

{для этого состояния допустимые переходы отсутствуют}

Move := -1;

end;

end;

ScanLeadDigits : begin

case Move of

0 : {сохранить данное состояние для текущей цифры}

begin

if TDIsDigit(Ch) then

inc(StrInx) else

inc(Move);

end;

1 : {переход к ScanDecPoint с использованием десятичного разделителя}

begin

if (Ch = DecimalSeparator) then begin

PushChoice(ChoiceStack, StrInx, Move, State);

State := ScannedDecPoint;

Move := 0;

inc(StrInx);

end else

inc(Move);

end;

else

{для этого состояния допустимые переходы отсутствуют}

Move := -1;

end;

end;

ScannedDecPoint : begin

case Move of

0 : {сохранить данное состояние для текущей цифры}

begin

if TDIsDigit(Ch) then

inc(StrInx) else inc(Move);

end;

else

{для этого состояния допустимые переходы отсутствуют}

Move := -1;

end;

end;

ScanLeadDecPoint : begin

case Move of

0 : {переход к ScanDecPoint с использованием цифры}

begin

if TDIsDigit(Ch) then begin

PushChoice(Choicestack, StrInx, Move, State);

State := ScanDecimalDigits;

Move := 0;

inc(StrInx);

end else

inc(Move);

end;

else

{для этого состояния допустимые переходы отсутствуют}

Move := -1;

end;

end;

ScanDecimalDigits : begin

case Move of

0 : {сохранить данное состояние для текущей цифры}

begin

if TDIsDigit(Ch) then

inc(StrInx) else inc(Move);

end;

else

{для этого состояния допустимые переходы отсутствуют}

Move := -1;

end;

end;

end;

{если для конкретного состояния допустимые переходы отсутствуют, выполнить отход за счет отказа от последнего выбора, и выполнить переход со следующим номером}

if (Move = -1) then begin

{если стек пуст, возможность выполнения отхода отсутствует}

if Choicestack.IsEmpty then

Exit;

{отказаться от последнего выбора, выполнить следующий по порядку переход}

PopChoice(ChoiceStack, StrInx, Move, State);

inc(Move);

end;

end;

{в этой точке число допустимо, если текущее состояние является конечным}

if (State = Scanlnteger) or

(State = ScannedDecPoint) or (State = ScanDecimalDigits) then

Result := true;

finally

ChoiceStack.Free;

end;

end;

Исходный код подпрограммы IsValidNumberNFA можно найти на web-сайте издательства, в разделе материалов. После выгрузки материалов отыщите среди них файл TDStates.pas.

Из листинга 10.3 видно, что базовая структура кода реализации всех состояний одинакова. Предполагается, что для каждого состояния существует ряд переходов, начиная с 0 (на рис. 10.3 переходы пронумерованы по ходу часовой стрелки). Для каждого состояния поочередно выполняется проверка возможности выполнения каждого из переходов. Если переход можно выполнить, сделанный выбор заталкивается в стек, после чего переход выполняется. Если переход невозможен, предпринимается попытка выполнения следующего перехода.

Если нужно осуществить отход, мы выталкиваем верхний выбор из стека и проверяем возможность выполнения следующего перехода. Хранящаяся в стеке информация достаточна для восстановления состояния подпрограммы, существовавшего в момент выбора.

Для сравнения на рис. 10.4 показана блок-схема детерминированного автомата, который выполняет эту же проверку, а код, реализующий его, приведен в листинге 10.4.

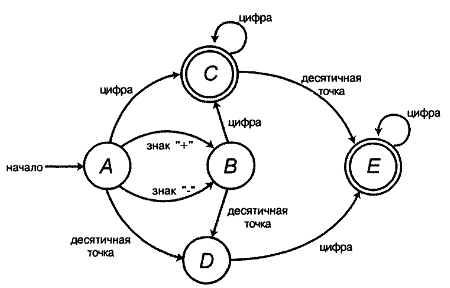
Рисунок 10.4. DFA-автомат для проверки, является ли строка числом

Листинг 10.4: Проверка того, что строка является числом, с помощью DFA-автомата

function IsValidNumber(const S : string) : boolean;

type

TStates = (StartState, GotSign,

GotInitDigit, GotInitDecPt, ScanDigits);

var

State : TStates;

Inx : integer;

Ch : AnsiChar;

begin

{предположим, что число является недопустимым}

Result := false;

{подготовиться к сканированию}

State := StartState;

{считывание всех символов строки}

for Inx := 1 to length(S) do

begin

{извлечь текущий символ}

Ch := S[Inx];

{обработать в зависимости от состояния}

case State of

StartState : begin

if (Ch = '+') or (Ch = '-') then

State := GotSign else

if (Ch = DecimalSeparator) then

State := GotInitDecPt else

if TDIsdigit(Ch) then

State := GotInitDigit else

Exit;

end;

GotSign : begin

if (Ch = DecimalSeparator) then

State := GotInitDecPt else

if TDIsDigit(Ch) then

State := GotInitDigit else Expend;

GotInitDigit : begin

if (Ch = DecimalSeparator) then

State := ScanDigits else

if not TDIsDigit(Ch) then

Exit;

end;

GotInitDecPt : begin

if TDIsDigit(Ch) then

State := ScanDigits else Expend;

ScanDigits : begin

if not TDIsDigit (Ch) then

Exit;

end;

end;

end;

{в этой точке число допустимо, если текущее состояние является конечным}

if (State = GotInitDigit) or (State = ScanDigits) then

Result := true;

end;

Исходный код подпрограммы IsValidNumber можно найти на Web-сайте издательства, в разделе материалов. После выгрузки материалов отыщите среди них файл TDStates.

Если сравнить коды, приведенные в листингах 10.3 и 10.4, невозможно не заметить, что код NFA-автомата значительно сложнее. Он содержит целый набор вспомогательных подпрограмм, которые необходимо закодировать и поддерживать. Он также более чреват ошибками (необходимо побеспокоиться о поддержке стека, о возврате конечного автомата к предшествующему состоянию, о выборе следующего перехода и т.п.).

В общем случае, если требуется фиксированный, заранее определенный автомат, следует попытаться разработать и использовать детерминированный автомат. Следует попытаться свести реализацию недетерминированных автоматов к автоматическим алгоритмам. Реализация их вручную - чересчур трудоемкая задача.

Конечно, в рассмотренном примере NFA-автомат (и в примере его аналога DFA-автомата) мы всего лишь проверяем, является ли строка текстовым описанием целого числа или числа с плавающей точкой. Обычно желательно также вычислить интересующее число, а это усложняет код реализации переходов. Реализация этой функции при использовании DFA-автомата достаточно проста. Мы устанавливаем значение аккумуляторной (накопительной) переменной равным 0. При декодировании каждой цифры, расположенной перед десятичной точкой, мы умножаем значение аккумуляторной переменной на 10.0 и добавляем к нему значение новой цифры. Для цифр, следующих за десятичной точкой, мы поддерживаем значение счетчика текущего десятичного разряда и увеличиваем его на единицу при считывании каждой цифры. Для каждой такой цифры мы добавляем ее значение, умноженное на 0.1 в степени, соответствующей достигнутой десятичной позиции.

А как насчет NFA-автомата? Что ж, в этом случае решить задачу достаточно трудно. Вся сложность обусловлена необходимостью реализации алгоритма отхода. В любой момент времени внезапно может оказаться, что необходимо вернуться к предыдущему состоянию. В примере преобразования строки в число с плавающей точкой это не очень страшно: при заталкивании выбора в стек достаточно сохранить в нем и текущее значение аккумуляторной переменной (и значения всех необходимых дополнительных переменных). При выполнении отхода в качестве данных для восстановления состояния в момент неудачного выбора мы вытолкнем из стека и значение накопительной переменной.

Оглавление книги