Книга: Феномен науки. Кибернетический подход к эволюции

11.2. Геометрическая алгебра

11.2. Геометрическая алгебра

На рис. 11.1 показана хорошо известная геометрическая трактовка соотношения

(a + b)² = a² + 2ab + b².

Столь же тривиальное с алгебраической точки зрения равенство

(a + b)(a - b) = a² - b²

требует уже более сложного геометрического рассмотрения. Ему соответствует следующая теорема во второй книге «Начал» Евклида (рис. 11.2):

«Если прямая линия разделена на равные и неравные части, то прямоугольник, содержащийся между неравными частями¹ всей прямой, вместе с квадратом отрезка между точками деления равен квадрату на половине прямой».

Доказывается теорема следующим образом.

Прямоугольник ABFE равен прямоугольнику BDHF. Прямоугольник BCGF равен прямоугольнику GHKJ. Если к этим двум прямоугольникам (образующим вместе прямоугольник ACGE, «содержащийся между неравными частями всей прямой») добавить квадрат FGJI, то получится как раз квадрат BDKI, построенный «на половине прямой». Итак, мы имеем равенство

(a + b)(a - b) + b² = a²,

эквивалентное приведенному выше, но не содержащее трудно интерпретируемого вычитания площадей.

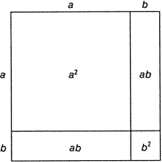
Рис. 11.1. Геометрическая трактовка тождества (a + b)² = a² + 2ab + b²

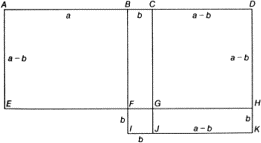
Рис. 11.2. Геометрическая трактовка тождества (a + b)(a - b) = a² - b²

Ясно, что если даже эти простейшие алгебраические соотношения требуют в геометрической трактовке определенных усилий для понимания формулировки теоремы и изобретательности для ее доказательства, то далеко по этому пути продвинуться невозможно. Во всем, что касается собственно геометрии, греки проявили себя как искуснейшие мастера. Но та линия развития математики, которая началась с алгебры, а затем породила анализ бесконечно малых и современные аксиоматические теории, т. е. линия, связанная с использованием не языка фигур, а языка символов, оказалась им совершенно недоступной. Греческая математика осталась ограниченной, сдавленной узкими рамками понятий, имеющих наглядный геометрический смысл.

Оглавление книги