Книга: Системное программное обеспечение. Лабораторный практикум

Грамматики предшествования

Грамматики предшествования

КС-языки делятся на классы в соответствии со структурой правил их грамматик. В каждом из классов налагаются дополнительные ограничения на допустимые правила грамматики. Одним из таких классов является класс грамматик предшествования. Они используются для синтаксического разбора цепочек с помощью модификаций алгоритма «сдвиг-свертка».

Принцип организации распознавателя на основе грамматики предшествования исходит из того, что для каждой упорядоченной пары символов в грамматике устанавливается отношение, называемое отношением предшествования. В процессе разбора МП-автомат сравнивает текущий символ входной цепочки с одним из символов, находящихся на верхушке стека автомата. В процессе сравнения проверяется, какое из возможных отношений предшествования существует между этими двумя символами. В зависимости от найденного отношения выполняется либо сдвиг, либо свертка. При отсутствии отношения предшествования между символами алгоритм сигнализирует об ошибке.

Задача заключается в том, чтобы иметь возможность непротиворечивым образом определить отношения предшествования между символами грамматики. Если это возможно, то грамматика может быть отнесена к одному из классов грамматик предшествования.

Отношения предшествования будем обозначать знаками «=.», «<.» и «.>». Отношение предшествования единственно для каждой упорядоченной пары символов. При этом между какими-либо двумя символами может и не быть отношения предшествования – это значит, что они не могут находиться рядом ни в одном элементе разбора синтаксически правильной цепочки. Отношения предшествования зависят от порядка, в котором стоят символы, и в этом смысле их нельзя путать со знаками математических операций (хотя по внешнему виду они очень похожи) – они не обладают ни свойством коммутативности, ни свойством ассоциативности. Например, если известно, что В_i.> В_j, то не обязательно выполняется В_j <. В_i (поэтому знаки предшествования помечают специальной точкой: «=.», «<.», «.>»).

Метод предшествования основан на том факте, что отношения предшествования между двумя соседними символами распознаваемой строки соответствуют трем следующим вариантам:

• В_i <. B_i+1, если символ B_i+1 – крайний левый символ некоторой основы (это отношение между символами можно назвать «предшествует основе» или просто «предшествует»);

• В_i.> B_i+1, если символ В_i – крайний правый символ некоторой основы (это отношение между символами можно назвать «следует за основой» или просто «следует»);

• В_i =. В_i+1, если символы В_i и В_i+1 принадлежат одной основе (это отношение между символами можно назвать «составляют основу»).

Исходя из этих соотношений выполняется разбор входной строки для грамматик предшествования.

Суть принципа такого разбора поясняет рис. 3.1. На нем изображена входная цепочка символов ???? в тот момент, когда выполняется свертка цепочки ?. Символ ? является последним символом подцепочки ?, а символ b – первым символом подцепочки ?. Тогда, если в грамматике удастся установить непротиворечивые отношения предшествования, то в процессе выполнения разбора по алгоритму «сдвиг-свертка» можно всегда выполнять сдвиг до тех пор, пока между символом на верхушке стека и текущим символом входной цепочки существует отношение <. или =.. А как только между этими символами будет обнаружено отношение.>, сразу надо выполнять свертку. Причем для выполнения свертки из стека надо выбирать все символы, связанные отношением =. Все различные правила в грамматике предшествования должны иметь различные правые части – это гарантирует непротиворечивость выбора правила при выполнении свертки.

Рис. 3.1. Отношения между символами входной цепочки в грамматике предшествования.

Таким образом, установление непротиворечивых отношений предшествования между символами грамматики в комплексе с несовпадающими правыми частями различных правил дает ответы на все вопросы, которые надо решить для организации работы алгоритма «сдвиг-свертка» без возвратов.

На основании отношений предшествования строят матрицу предшествования грамматики. Строки матрицы предшествования помечаются первыми (левыми) символами, столбцы – вторыми (правыми) символами отношений предшествования. В клетки матрицы на пересечении соответствующих столбца и строки помещаются знаки отношений. При этом пустые клетки матрицы говорят о том, что между данными символами нет ни одного отношения предшествования.

Существует несколько видов грамматик предшествования. Они различаются по тому, какие отношения предшествования в них определены и между какими типами символов (терминальными или нетерминальными) могут быть установлены эти отношения. Кроме того, возможны незначительные модификации функционирования самого алгоритма «сдвиг-свертка» в распознавателях для таких грамматик (в основном на этапе выбора правила для выполнения свертки, когда возможны неоднозначности) [1].

Выделяют следующие виды грамматик предшествования:

• простого предшествования;

• расширенного предшествования;

• слабого предшествования;

• смешанной стратегии предшествования;

• операторного предшествования.

Далее будут рассмотрены ограничения на структуру правил и алгоритмы разбора для грамматик операторного предшествования.

Матрицу операторного предшествования КС-грамматики можно построить, опираясь непосредственно на определения отношений предшествования [1, 3, 7], но проще и удобнее воспользоваться двумя дополнительными типами множеств – множествами крайних левых и крайних правых символов, а также множествами крайних левых терминальных и крайних правых терминальных символов для всех нетерминальных символов грамматики.

Если имеется КС-грамматика

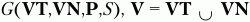
то множества крайних левых и крайних правых символов определяются следующим образом:

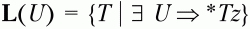
– множество крайних левых символов относительно нетерминального символа U;

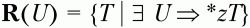
– множество крайних правых символов относительно нетерминального символа U,

где U – заданный нетерминальный символ

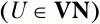
T – любой символ грамматики

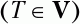
а z – произвольная цепочка символов (

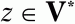
цепочка z может быть и пустой цепочкой).

Множества крайних левых и крайних правых терминальных символов определяются следующим образом:

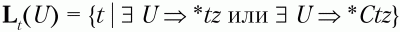
– множество крайних левых терминальных символов относительно нетерминального символа U;

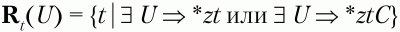
– множество крайних правых терминальных символов относительно нетерминального символа U,

где t – терминальный символ

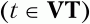
U и С – нетерминальные символы (U,

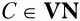
а z – произвольная цепочка символов (

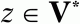
цепочка z может быть и пустой цепочкой).

Множества L(U) и R(U) могут быть построены для каждого нетерминального символа

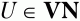
по очень простому алгоритму:

1. Для каждого нетерминального символа U ищем все правила, содержащие U в левой части. Во множество L(U) включаем самый левый символ из правой части правил, а во множество R(U) – самый правый символ из правой части (то есть во множество L(U) записываем все символы, с которых начинаются правила для символа U, а во множество R(U) – символы, которыми эти правила заканчиваются). Если в правой части правила для символа U имеется только один символ, то он должен быть записан в оба множества – L(U) и R(U).

2. Для каждого нетерминального символа U выполняем следующее преобразование: если множество L(U) содержит нетерминальные символы грамматики [U', U', …, то его надо дополнить символами, входящими в соответствующие множества L(U'), L(U')… и не входящими в L(U). Ту же операцию надо выполнить для R(U). Фактически, если какой-то символ U' входит в одно из множеств для символа U, то надо объединить множества для U' и U, а результат записать во множество для символа U.

3. Если на предыдущем шаге хотя бы одно множество L(U) или R(U) для некоторого символа грамматики изменилось, то надо вернуться к шагу 2, иначе – построение закончено.

Для нахождения множеств L_t(U) и R_t(U) используется следующий алгоритм:

1. Для каждого нетерминального символа грамматики U строятся множества L(U) и R(U).

2. Для каждого нетерминального символа грамматики U ищутся правила вида U ? tz и U ? Ctz, где

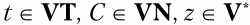
терминальные символы t включаются во множество L_t(U). Аналогично для множества R_t(U) ищутся правила вида U ? zt и U ? ztC (то есть во множество L_t(U) записываются все крайние слева терминальные символы из правых частей правил для символа U, а во множество R_t(U) – все крайние справа терминальные символы этих правил). Не исключено, что один и тот же терминальный символ будет записан в оба множества – L_t(U) и R_t(U).

3. Просматривается множество L(U), в которое входят символы U', U' … Множество L_t(U) дополняется терминальными символами, входящими в L_t(U'), L_t(U')… и не входящими в L_t(U). Аналогичная операция выполняется и для множества R_t(U) на основе множества R(U).

Для практического использования матрицу предшествования дополняют терминальными символами

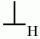
и

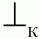
(начало и конец цепочки). Для них определены следующие отношения предшествования:

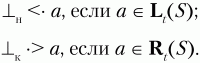
Имея построенные множества L_t(U) и R_t(U), заполнение матрицы операторного предшествования для КС-грамматики G(VT,VN,P,S) можно выполнить по следующему алгоритму:

1. Берем первый символ из множества терминальных символов грамматики VT:

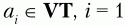
Будем считать этот символ текущим терминальным символом.

2. Во всем множестве правил Р ищем правила вида C ? xa_iby или C ? xa_iUb_jy, где а_i – текущий терминальный символ, Ь_j – произвольный терминальный символ

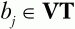
U и С – произвольные нетерминальные символы

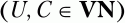
а х и у – произвольные цепочки символов, возможно пустые

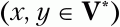
Фактически производится поиск таких правил, в которых в правой части символы а_i и Ъ_j стоят рядом или же между ними есть не более одного нетерминального символа (причем символ а_i обязательно стоит слева от Ь_j).

3. Для всех символов Ь_j, найденных на шаге 2, выполняем следующее: ставим знак «=.» («составляет основу») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом а_i, и столбца, помеченного символом b_j.

4. Во всем множестве правил Р ищем правила вида С ? xa_iU_jy, где а_i – текущий терминальный символ, U_j и С– произвольные нетерминальные символы (U_j,

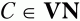
а х и у – произвольные цепочки символов, возможно пустые

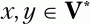
Фактически ищем правила, в которых в правой части символ а_i стоит слева от нетерминального символа U_j.

5. Для всех символов U_j, найденных на шаге 4, берем множество символов L_t(U_j). Для всех терминальных символов c_k, входящих в это множество, выполняем следующее: ставим знак «<.» («предшествует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом a_i, и столбца, помеченного символом с_k.

6. Во всем множестве правил Р ищем правила вида С ? xU_ja_iy, где a_i – текущий терминальный символ, U_j и С – произвольные нетерминальные символы

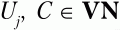
а x и y – произвольные цепочки символов, возможно пустые

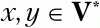
Фактически ищем правила, в которых в правой части символ а стоит справа от нетерминального символа U_j.

7. Для всех символов U_j, найденных на шаге 6, берем множество символов R_t(U_j). Для всех терминальных символов c_k, входящих в это множество, выполняем следующее: ставим знак «.>» («следует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом с_k, и столбца, помеченного символом а_i.

8. Если рассмотрены все терминальные символы из множества VT, то переходим к шагу 9, иначе – берем очередной символ

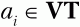
из множества VT, i:= i + 1, делаем его текущим терминальным символом и возвращаемся к шагу 2.

9. Берем множество L_t(S) для целевого символа грамматики S. Для всех терминальных символов c_k, входящих в это множество, выполняем следующее: ставим знак «<.» («предшествует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом

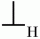
(«начало строки»), и столбца, помеченного символом c_k.

10. Берем множество R_t(S) для целевого символа грамматики S. Для всех терминальных символов c_k, входящих в это множество, выполняем следующее: ставим знак «.>» («следует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом c_k, и столбца, помеченного символом

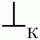
(«конец строки»). Построение матрицы закончено.

Если на всех шагах алгоритма построения матрицы операторного предшествования не возникло противоречий, когда в одну и ту же клетку матрицы надо записать два или три различных символа предшествования, то матрица построена правильно (в каждой клетке такой матрицы присутствует один из символов предшествования – «=.», «<.» или «.>» – или же клетка пуста). Если на каком-то шаге возникло противоречие, значит, исходная КС-грамматика G(VT,VN,P,S) не является грамматикой операторного предшествования. В этом случае можно попробовать преобразовать грамматику так, что она станет удовлетворять требованиям операторного предшествования (что не всегда возможно), либо необходимо использовать другой тип распознавателя.

Более подробно работа с грамматиками предшествования и другими типами распознавателей описана в [1–4, 7].

Оглавление книги