Книга: Основы объектно-ориентированного программирования
Формализация спецификаций
Представленный выше беглый набросок абстракции данных слишком неформален, чтобы его можно было постоянно использовать. Вернемся к нашему главному примеру. Стек, как мы это поняли, должен определяться в терминах применимых к нему операций, но тогда нам нужно определить эти операции!
Приведенные содержательные описания явно недостаточны - put вталкивает элемент на "вершину" стека, remove выталкивает элемент, находящийся на вершине. Нам нужно точно знать, как клиенты могут использовать эти операции и что они для этого должны делать.
Спецификация АТД предоставит эту информацию. Она состоит из четырех разделов, разъясняемых в следующих разделах:
[x]. ТИПЫ
[x]. ФУНКЦИИ
[x]. АКСИОМЫ
[x]. ПРЕДУСЛОВИЯ
Для спецификации АТД в этих разделах будут использоваться простая математическая нотация.
| Эту нотацию - математический формализм - не надо путать с программной нотацией в остальной части книги, даже если для согласования она использует тот же стиль синтаксиса. У нее нет специального имени, и она не является нотацией языка программирования. Она могла бы послужить отправной точкой для формального языка спецификаций, но мы удовлетворимся использованием не требующих объяснения соглашений для однозначной спецификации АТД. |
Специфицирование типов
В разделе ТИПЫ указываются специфицируемые типы. В общем случае, может оказаться удобным определять одновременно несколько АТД, хотя в нашем примере имеется лишь один тип STACK(СТЕК). Между прочим, что такое тип? Ответ на этот вопрос объединит все положения, развиваемые далее в этой лекции: тип - это совокупность объектов, характеризуемая функциями, аксиомами и предусловиями. Не будет большой ошибкой рассматривать пока тип как множество объектов в математическом смысле слова "множество" - тип STACK как множество всех возможных стеков, тип INTEGER как множество всех целых чисел и т.д.
Однако при этом не должно быть никакой путаницы: АТД, такой как STACK, - это не объект (один конкретный стек), а совокупность объектов (множество всех стеков). Напомним, в чем состоит наша главная цель: найти подходящую основу для модулей наших программных систем. Очевидно, не имеет смысла делать основой для модуля один конкретный объект - один стек, один самолет, один счет в банке. ОО-проектирование даст нам возможность строить модули, отражающие свойства всех стеков, всех самолетов, всех банковских счетов, или, по крайней мере, значительной их части.
Объект, принадлежащий множеству объектов, описываемых спецификацией АТД, называется экземпляром этого АТД. Например, конкретный стек, обладающий свойствами абстрактного типа данных STACK, будет экземпляром АТД STACK. Понятие экземпляра проходит через все ОО-проектирование и программирование, и будет играть важную роль в объяснении поведения программ во время исполнения.
В разделе ТИПЫ просто перечисляются типы, вводимые в данной спецификации. Здесь:
Типы
[x]. STACK[G]
Таким образом, наша спецификация относится к одному абстрактному типу данных - STACK, задающему стеки объектов произвольного типа G.
Универсализация (Genericity)
В описании STACK[G] именем G обозначен произвольный, не определяемый тип. G называется формальным родовым параметром для типов элементов АТД STACK, а сам STACK называется родовым или универсальным АТД. Механизм, допускающий такие параметризованные спецификации, известен как универсализация, мы уже сталкивались с аналогичным понятием в обзоре конструкций пакетов.
Можно писать спецификации АТД без параметризации, но ценой будут неоправданные повторения. Кроме того, возможность повторного использования желательна не только для программ, но и для спецификаций! Благодаря механизму универсализации, можно выполнять параметризацию типов в явном виде, выбрав для параметра некоторое произвольное имя (здесь - G), представляющее переменную для типа элементов стека.
В результате такой АТД как STACK - это не просто тип, а скорее образец типа. Для получения непосредственно используемого типа стека нужно определить тип элементов стека, например ACCOUNT, и передать его в качестве фактического родового параметра, соответствующего формальному параметру G. Поэтому, хотя сам по себе STACK это образец типа, обозначение STACK[ACCOUNT] задает полностью определенный тип. Про такой тип, полученный с помощью передачи фактических параметров типов в родовой тип, говорят, что он порожден из общего по образцу.
Эти понятия можно применять рекурсивно: каждый тип должен, по крайней мере, в принципе, иметь спецификацию АТД, поэтому можно и тип ACCOUNT считать абстрактным типом данных. Кроме того, тип, подставляемый в качестве фактического параметра типа в STACK (для получения типа, порожденного по образцу) может и сам быть порожденным по образцу. Например, можно вполне корректно использовать обозначение STACK[STACK [ACCOUNT]] для определения соответствующего абстрактного типа данных: элементами этого типа являются стеки, элементами которых, в свою очередь, являются банковские счета.
Как показывает этот пример, предыдущее определение "экземпляра" нуждается в некоторой модификации. Строго говоря, конкретный стек является экземпляром не типа STACK (который, как мы заметили, является скорее образцом типа, а не типом), а некоторого типа, порожденного типом STACK, например, образцом типа STACK[ACCOUNT]. Тем не менее, нам удобно и далее говорить об экземплярах типа S и других образцов типов, понимая при этом, что речь идет об экземплярах порожденных ими типов.
Аналогично, не очень правильно говорить о типе STACK как об АТД: правильный термин в этом случае - "образец АТД". Но для простоты в данном обсуждении мы будем и далее, если это не приведет к путанице, опускать слово "образец".
Это отличие перенесется и на ОО-проектирование и программирование, но там нам не потребуется два разных термина:
[x]. Основным понятием будет класс, который может иметь родовые параметры.
[x]. Описание реальных данных требует типов. Класс без параметров является также и типом, но класс с параметрами - только образец типа. Чтобы получить конкретный тип из такого класса, нужно передать ему фактические параметры типов, точно так, как мы это делали при получении АТД STACK[ACCOUNT], исходя из образца АТД STACK[G].
Перечисление функций
Вслед за разделом ТИПЫ идет раздел ФУНКЦИИ, в котором перечисляются операции, применяемые к экземплярам данного АТД. Как уже говорилось, эти операции будут главными компонентами определения типа, с их помощью описывается, что могут предложить его экземпляры, а не то, чем они являются.
Ниже приведен раздел ФУНКЦИИ для абстрактного типа данных STACK. Если вы разработчик ПО, то этот стиль описания вам знаком: строки этого раздела напоминают декларации типизированных языков программирования таких, как Pascal или Ada. Строка для операции new похожа на объявление переменной, остальные - на заголовки процедур.
Функции
[x]. put: STACK [G] ? G
[x]. remove: STACK [G]
[x]. item: STACK [G]
[x]. empty: STACK [G]
[x]. new: STACK [G]
В каждой строке вводится определенная математическая функция, моделирующая соответствующую операцию над стеком. Например, функция put представляет операцию, которая вталкивает элемент на вершину стека.
Почему функции? Большая часть программистов не посчитает такую операцию как put функцией. Когда во время работы программной системы операция put применяется к стеку, она, как правило, изменяет этот стек, добавляя к нему элемент. Вследствие этого в приведенной выше классификации операций put была "командой" - операцией, которая может модифицировать объекты. (Две другие категории операций - это конструкторы и запросы).
Однако спецификация АТД - это математическая модель и в ее основании должны быть корректные математические методы. В математике понятие команды или, более общно, изменение чего-либо как таковое отсутствует: вычисление квадратного корня из числа 2 не изменяет само это число. Математические выражения просто определяют одни математические объекты в терминах некоторых других математических объектов. В отличие от вычисления программы на компьютере, они никогда не изменяют никакие математические объекты. Но поскольку мы нуждаемся в некотором математическом объекте для моделирования операций компьютера, то понятие функции представляется наиболее близким приближением. Функция - это механизм для получения некоторого результата, принадлежащего некоторому результирующему множеству по любому допустимому входу, принадлежащему некоторому исходному множеству. Например, если R обозначает множество вещественных чисел, то определение функции
square_plus_one: R R
square_plus_one(x)= x2 + 1 (для каждого x из R)
вводит функцию square_plus_one, для которой R является и исходным и результирующим множеством и которая выдает для любого входа в качестве результата квадрат этого входа, увеличенный на 1.
Спецификации абстрактных типов данных используют именно это понятие. Например, операция put определяется как
put: STACK [G] ? G STACK [G]
и означает, что put будет брать два аргумента: STACK экземпляров типа G и экземпляр типа G и возвращать в качестве результата новый STACK [G]. (Более формально, множеством определения функции put является множество STACK [G] _ G, являющееся декартовым произведением множеств STACK [G] и G, т.е. множеством пар <s, x>, в которых первый элемент s принадлежит STACK [G] , а второй элемент x принадлежит G.) Вот рисунок, иллюстрирующий это:
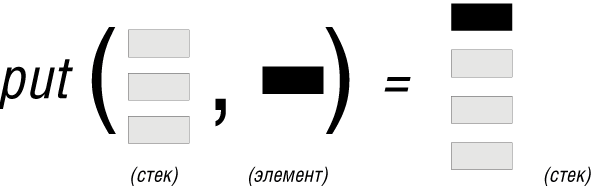
Рис. 6.3. Применение функции put
АТД имеют дело только с математическими функциями, у которых нет никаких побочных эффектов и которые, на самом деле, ничего не изменяют. Когда мы покинем утонченную сферу спецификации и попадем в неразбериху проектирования и реализации программ, нам придется восстановить понятие изменения, так как из-за накладных расходов мало кто одобрит программное окружение, в котором каждое выполнение операции "втолкнуть" в стек начинается с копирования этого стека. Мы рассмотрим позже переход от лишенного изменений мира АТД к полному изменений миру разработки ПО. Но поскольку сейчас мы хотим понять, как лучше всего определять типы, то математический взгляд на вещи нас вполне устраивает.
Из нашего обсуждения следуют роли операций, моделируемых каждой из функций спецификации STACK:
[x]. Функция put возвращает новое состояние стека с одним новым элементом, помещенным на его вершину. Рисунок на предыдущей странице иллюстрирует операцию put(s, x), выполняемую над стеком s и элементом x.
[x]. Функция remove возвращает новое состояние стека с вытолкнутым верхним элементом, если таковой был. Как и put, эта функция при проектировании и реализации должна превращаться в команду (операцию, изменяющую объект, обычно реализуемую как процедура). Мы увидим далее, как учесть возможность пустого стека, с вершины которого нечего удалять.
[x]. Функция item возвращает верхний элемент стека, если таковой имеется.
[x]. Функция empty выявляет пустоту стека, ее результатом является логическое значение (истина или ложь). Предполагается, что АТД BOOLEAN, задающий логические значения, определен отдельно.
[x]. Функция new создает пустой стек.
В разделе ФУНКЦИИ эти функции определяются не полностью, вводятся только их сигнатуры - списки типов их аргументов и результата. Сигнатура функции put
STACK [G] ? G STACK [G]
показывает, что put берет в качестве аргумента пару вида <s,x>, в которой s - экземпляр типа STACK [G], а x - экземпляр типа G, и возвращает в качестве результата экземпляр типа STACK [G]. Вообще говоря, множество значений функции (его тип указывается в сигнатуре правее стрелки, здесь это STACK [G]) может само быть декартовым произведением. Это можно использовать при описании операций, возвращающих два или более результатов.
В сигнатуре функций remove и item вместо обычной стрелки используется перечеркнутая стрелка
new: STACK
без всякой стрелки в сигнатуре. Фактически, это сокращение для записи
new: STACK,
определяющей функцию без аргументов. Здесь аргументы не нужны, поскольку new должна всегда возвращать один и тот же результат - пустой стек. Поэтому для простоты мы убрали здесь стрелку. Результат применения этой функции (т. е. пустой стек) будет записываться new, как сокращение для new(), обозначающего результат применения new к пустому списку аргументов.
Категории функций
В начале этой лекции операции над типами были разделены на конструкторы, запросы и команды. В спецификации АТД для нового типа T, например для STACK [G] в нашем примере можно определить эту классификацию более строго. Эта классификация просто проверяет, где по отношению к стрелке расположен в сигнатуре каждой функции тип T:
| В альтернативной терминологии эти три категории называются "конструктор", "аксессор" и "модификатор". Здесь мы придерживаемся терминов, более непосредственно связанных с интерпретацией функций АТД как моделей операций над программными объектами. |
[x]. Функция, в сигнатуре которой T появляется лишь справа от стрелки, например new, является функцией-конструктором. Она моделирует операцию, создающую экземпляры T из экземпляров других типов или вообще не использующую аргументов, например как в случае константного конструктора new.
[x]. Такие функции как item и empty, у которых T появляется только слева от стрелки, являются функциями-запросами. Они моделируют операции, которые устанавливают свойства T, выраженные в терминах экземпляров других типов (в наших примерах - это BOOLEAN и параметр типа G).
[x]. Такие функции как put и remove, у которых T появляется с обеих сторон стрелки, являются функциями-командами. Они моделируют операции, которые по существующим экземплярам T и, возможно, экземплярам других типов выдают новые экземпляры типа T.
Раздел АКСИОМЫ
Мы уже видели, как типы данных (например, STACK) описываются посредством задания списка функций, применимых к их экземплярам. Все, что известно об этих функциях, - это их сигнатуры.
Чтобы указать, что речь идет о стеке, а не какой-либо другой структуре данных, имеющейся пока спецификации АТД совершенно недостаточно. Всякий распределитель, например очередь: "первым вошел - первым вышел", также будет удовлетворять этой спецификации.
Это, конечно, не должно удивлять, поскольку в разделе ФУНКЦИИ сами функции только объявляются (так же, как в программе объявляются переменные), но полностью не определяются. В ранее рассмотренном примере математического определения:
square_plus_one: R R
square_plus_one (x)= x2 + 1 (для каждого x из R)
первая строка играет роль сигнатуры, но есть еще и вторая строка, в которой определяется значение функции. Как можно достичь того же для функций АТД?
Мы не будем использовать явные определения в духе второй строки определения функции square_plus_one, потому что это заставило бы нас выбрать интерпретацию, а все предшествующее обсуждение показало нам опасность раннего выбора представления.
Только чтобы убедиться в том, что мы понимаем, как может выглядеть явное определение, давайте напишем одно такое определение для приведенного ранее представления стека МАССИВ_ВВЕРХ. С точки зрения математики выбор этого представления означает, что экземпляр типа STACK - это пара <count, representation> , где representation - это массив, а count - это число помещенных в стек элементов. Тогда явное определение функции put (для любого экземпляра x типа G) выглядит так:
put (<count, representation>, x)= <count + 1, representation [count+1: x]>
где a [n: v] обозначает массив, полученный из a путем изменения значения элемента с индексом n на v (все остальные элементы не изменяются).
Это определение функции put является просто математической версией реализации операции put, набросок которой в стиле Паскаля приведен вслед за представлением МАССИВ_ВВЕРХ на рисунке с возможными представлениями стеков в начале этой лекции.
Но это не то определение, которое бы нас устроило. "Освободите нас от рабства представлений!" - этот лозунг Фронта Освобождения Объектов и его военного крыла (бригады АТД) является также и нашим. (Отметим, что его политическая ветвь специализируется на тяжбах: класс - действие).
Поскольку всякое явное определение заставляет выбирать некоторое представление, обратимся к неявным определениям. При этом воздержимся от определения значений функций в спецификации АТД и вместо этого опишем свойства этих значений - все их существенные свойства, но только эти свойства.
Они формулируются в разделе АКСИОМЫ (AXIOMS). Для типа STACK он выглядит следующим образом.
Аксиомы
Для всех x: G, s: STACK [G],
[x]. (A1) item (put (s, x)) = x
[x]. (A2) remove (put (s, x)) = s
[x]. (A3) empty (new)
[x]. (A4) not empty (put (s, x))
Первые две аксиомы выражают основные свойства стеков (последним пришел - первым ушел) LIFO. Чтобы понять их, предположим, что у нас есть стек s и экземпляр x, и определим s' как результат put(s, x) , т. е. как результат вталкивания x в s. Приспособим один из предыдущих рисунков:
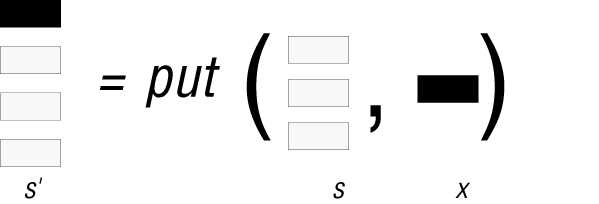
Рис. 6.4. Применение функции put
Здесь аксиома A1, говорит о том, что вершиной s' является x - последний элемент, который мы втолкнули, а аксиома A2 объясняет, что при удалении верхнего элемента s' мы снова получаем тот же стек s, который был до вталкивания x. Эти две аксиомы дают лаконичное описание главного свойства стеков в чисто математических терминах без всякой помощи императивных рассуждений или ссылок на свойства представлений.
Аксиомы A3 и A4 говорят о том, когда стек пуст, а когда - нет: стек, полученный в результате работы конструктора new пустой, а всякий стек, полученный после вталкивания элемента в уже существующий стек (пустой или непустой) не является пустым.
Эти аксиомы, как и остальные, являются предикатами (в смысле логики), выражающими истинность некоторых свойств для всех возможных значений s и x. Некоторые предпочитают рассматривать A3 и A4 в другой эквивалентной форме как определение функции empty индукцией по размеру стеков:
Для всех x: G, s: STACK [G]
A3' · empty (new) = true
A4' · empty (put (s, x)) = false
Две или три вещи, которые мы знаем о стеках
Спецификации АТД являются неявными. Имеются два вида "неявности":
[x]. Метод АТД определяет неявно некоторое множество объектов, задавая применимые к ним функции. Из этого определения никогда не следует, что в нем перечислены все операции; часто, на пути к представлению, будут добавлены и другие.
[x]. Сами функции также определяются неявно. Вместо явных определений используются аксиомы, задающие свойства этих функций. Здесь тоже ничего не утверждается о полноте: когда вы, в конце концов, дойдете до реализации этих функций, они приобретут дополнительные свойства.
Эта неявность является ключевым аспектом абстрактных типов данных и, как следствие, - их будущих аналогов в построении ОО-ПО - классов. Когда мы определяем абстрактный тип данных или класс, мы всегда сообщаем кое-что об этом типе или классе, просто перечисляя те их свойства, которые знаем, и берем их в качестве определения. При этом никогда не предполагается, что других применимых свойств нет.
Неявность также предполагает открытость определений: всегда можно добавить новые свойства АТД или класса. Основным механизмом для выполнения таких расширений без разрушения уже существующего первоначального определения является наследование.
Этот "неявный" подход имеет далеко идущие последствия. В пункте "дополнительные темы" в конце этой лекции помещены еще некоторые комментарии о неявности.
Частичные функции
Спецификация всякого реалистичного примера, даже такого простого как стеки, неизбежно сталкивается с проблемами не всюду определенных операций: некоторые операции применимы не ко всем возможным элементам исходных множеств. Например, это имеет место для функций remove и item: нельзя удалить элемент из пустого стека, и у пустого стека нет верхнего элемента.
Решение этой проблемы, использованное в приведенной выше спецификации, состоит в том, чтобы определить эти функции как частичные. Функция из исходного множества X в результирующее множество Y является частичной, если она определена не для всех элементов X. Функция, не являющаяся частичной, называется полной. Простым примером частичной функции в обычной математике является функция обращения действительных чисел inv, значение которой на действительном числе x равно
inv(x)= 1/x.
Поскольку inv не определена при x = 0, мы можем определить ее как частичную функцию на множестве R всех действительных чисел:
Inv: R R
Чтобы указать, что функция частичная, используется перечеркнутая стрелка
Областью (определения) частичной функции типа X
В спецификации АТД STACK эти идеи использованы для стеков при объявлении remove и item как частичных функций в разделе ФУНКЦИИ - это указано с помощью перечеркнутых стрелок в их сигнатуре. При этом возникает новая проблема, обсуждаемая в следующем пункте: как задавать области таких функций?
В некоторых случаях функцию put тоже желательно описывать как частичную, например, это требуется в таких реализациях как МАССИВ_ВВЕРХ и МАССИВ_ВНИЗ, которые поддерживают выполнение лишь конечного числа подряд идущих операций put для каждого заданного стека. Это на самом деле полезное упражнение - приспособить спецификацию STACK к тому, чтобы она описывала ограниченные стеки конечного объема, поскольку в приведенном выше виде она не содержит никаких ограничений на размеры стеков.
Это будет новым применением частичных функций, отражающим ограничения реализации. В отличие от этого, объявление функций remove и item как частичных отражает абстрактное свойство этих операций, относящееся ко всем реализациям.
Предусловия
Частичные функции являются неустранимым фактом процесса проектирования ПО, отражающим очевидное наблюдение: не каждая операция применима ко всем объектам. Но они также являются и потенциальным источником ошибок: если функция f из X в Y является частичной, то нельзя быть уверенным в том, что выражение f(e) имеет смысл, даже если e принадлежит X - требуется гарантировать, что это значение принадлежит области f.
Для этого всякая спецификация АТД, содержащая частичные функции, должна задавать их области. В этом и состоит роль раздела ПРЕДУСЛОВИЯ (PRECONDITIONS). Для АТД STACK этот раздел выглядит так:
Предусловия (preconditions)
[x]. remove (s: STACK [G]) require not empty (s)
[x]. item (s: STACK [G]) require not empty (s)
В нем у каждой из функций в пункте "требует" перечисляются условия, которым должны удовлетворять аргументы функции, чтобы входить в ее область.
Булевское выражение, которое определяет область функции, называется предусловием соответствующей частичной функции. В нашем случае предусловия обеих функций remove и item утверждают, что стек должен быть непустым. Перед "требует" помещается имя функции с именами ее аргументов (в примере для аргумента-стека использовано s), так что предусловие может ссылаться на эти аргументы.
| С точки зрения математики предусловие функции f - это характеристическая функция области f. Характеристической функцией подмножества Aмножества X называется полная функция ch: X |
Полная спецификация
Раздел ПРЕДУСЛОВИЯ (PRECONDITIONS) завершает простую спецификацию абстрактного типа данных STACK. Для удобства ссылок полезно собрать вместе разные компоненты спецификации, приведенные выше. Вот полная спецификация.
Спецификация стеков как АТД
ТИПЫ (TYPES)
[x]. STACK [G]
ФУНКЦИИ (FUNCTIONS)
[x]. put: STACK [G] ? G
[x]. remove: STACK [G]
[x]. item: STACK [G]
[x]. empty: STACK [G]
[x]. new: STACK [G]
АКСИОМЫ (AXIOMS)
Для всех x: G, s: STACK [G]
[x]. (A1) item (put (s, x)) = x
[x]. (A2) remove (put (s, x)) = s
[x]. (A3) empty (new)
[x]. (A4) not empty (put (s, x))
ПРЕДУСЛОВИЯ (PRECONDITIONS)
[x]. remove (s: STACK [G]) require not empty (s)
[x]. item (s: STACK [G]) require not empty (s)
Ничего кроме правды
Сила спецификаций АТД проистекает из их способности отражать только существенные свойства структур данных без лишних деталей. Приведенная выше спецификация стеков выражает все, что нужно по существу знать о понятии стека, и не включает ничего, что относилось бы к каким-либо конкретным реализациям стеков. Это вся правда о стеках, и ничего кроме правды.
Такие спецификации задают общую модель вычислений на соответствующих структурах данных. Определенные в спецификации абстрактного типа данных функции позволяют строить сложные выражения, а аксиомы АТД позволяют упрощать такие выражения и получать более простые результаты. Сложное стековое выражение является математическим эквивалентом программы, а процесс упрощения является математическим эквивалентом вычисления или выполнения этой программы.
Вот пример. Рассмотрим для приведенной выше спецификации АТД STACK следующее выражение stackexp:
item (remove (put (remove (put (put (
remove (put (put (put (new, x1), x2), x3)),
item (remove (put (put (new, x4), x5)))), x6)), x7)))
По-видимому, выражение stackexp будет проще понять, если мы представим его как последовательность вспомогательных выражений:
s1 = new
s2 = put (put (put (s1, x1), x2), x3)
s3 = remove (s2)
s4 = new
s5 = put (put (s4, x4), x5)
s6 = remove (s5)
y1 = item (s6)
s7 = put (s3, y1)
s8 = put (s7, x6)
s9 = remove (s8)
s10 = put (s9, x7)
s11 = remove (s10)
stackexp = item (s11)
Какой бы вариант определения вы ни выбрали, по нему несложно восстановить вычисление, математической моделью которого является stackexp: создать новый стек; втолкнуть в него элементы x1, x2, x3 (в указанном порядке); удалить верхний элемент (x3), назвав получившийся стек s3; создать другой пустой стек и т. д. Этот процесс графически представлен на рис. 6.5.
Можно легко найти значение такого АТД выражения, нарисовав последовательно несколько таких рисунков. (Здесь найдено x4). Но теория позволяет нам получить этот результат формально, не обращаясь к рисункам, а только последовательно применяя аксиомы для упрощения выражения, до тех пор, пока дальнейшее упрощение станет невозможным. Например:
[x]. Применить A2 для упрощения s3 - т. е. заменить remove(put (put (put (s1, x1), x2), x3)) на выражение put (put (s1, x1), x2)). (Согласно A2 всякую пару remove-put можно выбросить).
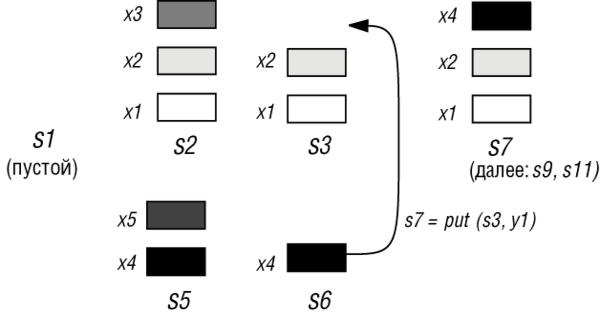
Рис. 6.5. Манипуляции со стеком
[x]. По той же аксиоме s6 равно put(s4, x4) . Затем можно применить аксиому A1 и вывести, что y1, т. е. item(put(s4, x4)) на самом деле равно x4, установив тем самым (как указано стрелкой на рисунке), что s7 получается в результате вталкивания x4 на верщину стека s3.
И так далее. Последовательность таких упрощений, выполненная механически так же легко и как последовательность упрощений в элементарной арифметике, приведет к значению выражения stackexp, которое действительно равно x4 (попробуйте проверить это сами, аккуратно проведя весь процесс упрощения).
Этот пример позволяет отметить одну из важнейших теоретических ролей абстрактных типов данных: они предоставляют формальную модель для понятий программы и выполнения программы. Эта модель чисто математическая: в ней нет императивных понятий состояния программы, переменных с изменяемыми во времени значениями, последовательности выполняемых действий. Она основана на обычных математических методах преобразования выражений.
- Глава 9 Моделирование и формализация
- 1.10. МОДЕЛИРОВАНИЕ И ПРОГРАММИРОВАНИЕ. ПОНЯТИЕ СПЕЦИФИКАЦИЙ
- Повторное использование проектов и спецификаций
- Выражение спецификаций
- 9.4. Формализация
- Создание спецификаций
- 12.11. Формализация теории множеств
- 14.4. Формализация научного языка
- 12.5. Формализация и метасистемный переход
- Лекция 6. Абстрактные типы данных (АТД)
- Специфика планирования в различных носителях




