Книга: Вычислительное мышление: Метод решения сложных задач

Выводим правила

Выводим правила

До сих пор мы выводили факты непосредственно из двух правил. Но решив много головоломок и обретя опыт, мы берем на вооружение другой подход — используем естественные навыки вычислительного мышления, например из ранее встречавшихся ситуаций. Этот метод позволяет решать головоломки быстрее и тратить меньше времени на их обдумывание. Следующий шаг — , то есть для поиска образцов мы расширяем круг ситуаций, а не возвращаемся к уже известным. При наличии опыта мы начинаем создавать новые, ускоренные и универсальные правила, которые позволяют вести логические рассуждения на более высоком уровне. Это становится возможным благодаря использованию не с целью решить конкретную головоломку, как мы делали до сих пор, но с целью создать новые правила. При этом мы уверены, что эти новые правила гарантированно выведены из основных. Давайте посмотрим, о чем идет речь, на некоторых примерах.

Вернемся к решению предыдущей головоломки. Мы выяснили, что, если в области содержится только один шестиугольник, в нем должна стоять 1. Это следует непосредственно из первого правила. Осознав, что нет необходимости снова это обдумывать, мы можем из начального правила вывести новое.

Чтобы наглядно представить это правило и не ограничиваться словами, мы набросаем схему (рис. 20). Стрелка показывает, какие изменения мы вносим в улей. Слева изображена позиция сопоставления с образцом, а справа — вносимые изменения, если найдем образец. Подобные правила называются или Наше правило в виде схемы показывает, что если мы найдем пустой участок в один шестиугольник, то можем преобразовать его в шестиугольник с 1.

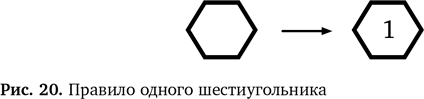
Теперь можно применять это правило, даже не задумываясь, почему оно работает. Наше логическое мышление теперь оперирует на более высоком уровне, по крайней мере в такой простой ситуации.

Теперь выведем еще одно новое правило для областей, состоящих из двух шестиугольников. Мы видели, что если есть область из двух шестиугольников и в одном стоит 2, то во второй нужно поставить 1 (рис. 21).

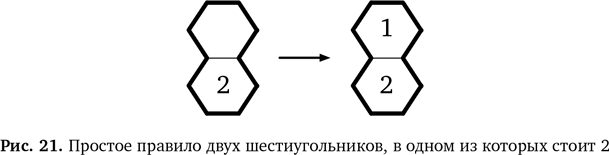
Мы вправе рассматривать это как правило из конкретного примера нашей головоломки. Не важно, в каком шестиугольнике стоит 2, — логика не меняется. Даже если картинку перевернуть, правило останется прежним. Это правило применимо и к шестиугольникам, соприкасающимся по диагонали в любом направлении. Но обобщение можно продолжить. По той же логике, если в области из двух шестиугольников в одном уже стоит 1, в другой нужно поставить 2. Это показано на рис. 22.

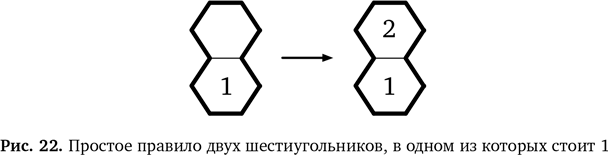
Объединив два эти отдельные правила, мы получаем полное обобщенное правило:

в другом шестиугольнике будет второе число из этих двух.

Правило можно представить в виде схемы, где будет обозначать любое число (точно так же, как математики используют и для обозначения переменных в алгебре).

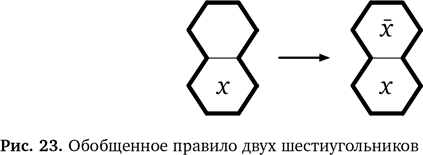
В одном случае заменяет 1, а в другом — 2, но замена остается неизменной в рамках одного примера. Схема правила приведена на рис. 23. На схеме обозначает другое число. То есть если x — это 1, то это 2 и если x — это 2, то 1. Это правило подходит для области из двух шестиугольников, повернутой в любую сторону, и не важно, какое число стоит наверху, а какое — внизу. Схема превращается в одно из изначальных правил (и их схем), если заменить на 1 или 2. Так мы начали изобретать своего рода математические обозначения, которые используются с той же целью, что и символы в математике. Они дают возможность говорить о вещах с большой точностью, и это важно, так как по мере усложнения правил надо стараться избегать возможных ошибок.

Вместо того чтобы выводить новые факты из заданных фактов, используя исходные правила решения головоломки, мы теперь выводим новые, «более крупные» правила с учетом исходных. Это называется Когда мы видим ситуацию, соответствующую образцу из какого-то нового правила, мы уже не думаем, почему оно верно, а просто применяем его. Мы от обоснования, стоящего за правилом.

Давайте рассмотрим последний пример создания более общего правила на базе нашего для решения простой головоломки. Оказывается, он весьма полезен. Мы поняли, куда поставить 1 в области из четырех шестиугольников в нижнем углу. Это было возможно, потому что в прилегающей области уже стояла 1, устроившаяся в углу, как показано на рис. 24.

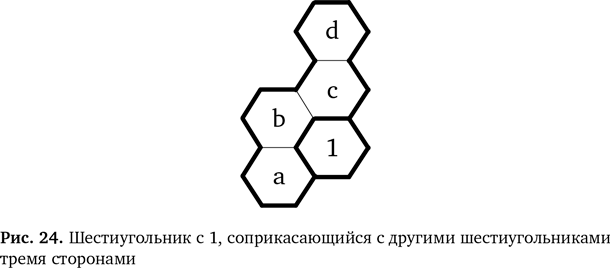
Единицу нужно поставить в позицию a, b, c или d (рис. 24). Однако в соответствии со вторым правилом головоломки рядом не должна находится ячейка с 1. Значит, позиции b и с исключаются. Остается только позиция d, и только туда получается поставить 1. Мы можем изобразить этот этап в виде схемы для правила замены (рис. 25).

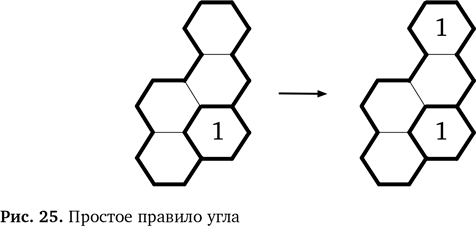
Конечно, в любых пустых шестиугольниках уже могут стоять числа, но правило остается справедливым — это еще один способ наше новое правило. Кроме того, число, которое мы используем при сопоставлении с образцом, необязательно должно быть 1. Это может быть любое другое число в рамках достаточно большой области. Если мы опять поставим на место любого возможного числа, то наше правило становится обобщенным вариантом (рис. 26).

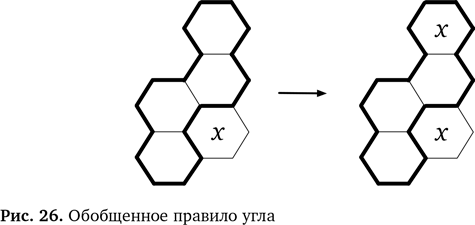
Мы даже можем продолжить обобщение нашего правила. Область, которую мы заполняем, не должна иметь заданную форму. Следующий шестиугольник может стоять в любой позиции у дальнего края более крупной области — везде, где он связан с угловым шестиугольником, но не касается его. В варианте правила угла на рис. 27 мы использовали вопросительные знаки, которые показывают возможные положения этого шестиугольника.

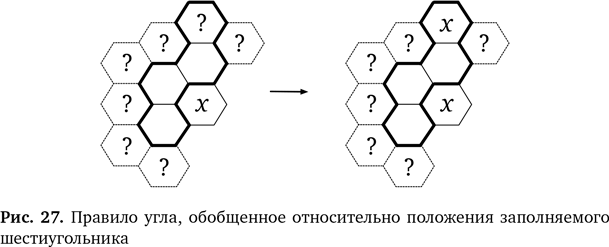
Получаем обобщенное правило:

Как и в предыдущих случаях, правило применимо при любом положении схемы — перевернутом, горизонтальном, под углом или отраженном. Возможно, вы найдете больше способов правило.

Итак, сейчас у вас есть вышеприведенное общее правило. Если в головоломке вы увидите ситуацию, сопоставимую с образцом, правило можно применить. Вставьте пропущенное число, которое соответствует

Большинство при решении головоломок не записывают правила, которые они выводят и используют. Люди просто запоминают сработавший метод и, особенно не задумываясь, по возможности применяют его. Однако специалисты по информатике любят записывать такое. Зачем это делать? Примерно по тем же причинам, что и записывать алгоритмы. Их можно использовать, например, чтобы научить других разгадывать головоломки (как это сделали мы), и тогда им не придется проходить весь этот путь с самого начала. Правила можно использовать, чтобы научить компьютер разгадывать головоломки. Кроме того, это делается ради точности. Довольно часто возникают ложные воспоминания о сработавших правилах, или мы можем выучить их, не до конца уловив детали. В любом случае в результате правило может использоваться неверно или в новой ситуации, которой оно не очень соответствует. Если записать все точно, то мы избежим такого рода ошибок.

Но здесь уже не получится использовать рисунки, как сейчас. В информатике для записи правил используют математические обозначения (). Языки для описания этой логики немного похожи на языки программирования, но при этом они очень гибкие. Их большое преимущество состоит в том, что их легко обработать на компьютере, и затем на их основе компьютер может строить логические рассуждения. Так логика становится основой для компьютерных программ, которые позволяют решать головоломки.

Многие системы искусственного интеллекта основаны на идее использования Вместо того чтобы рисовать схемы, мы пишем правила в следующем виде:

Список таких правил представляет собой программу. Если правило работает, то компьютер может выполнить действие. Если совпадают несколько правил, он выбирает любое, и все повторяется снова и снова. Такой подход обеспечивает новую парадигму для создания программ и позволяет совершенно по-другому увидеть их сущность. Это не просто последовательность команд для выполнения, о которой мы говорили до сего момента, а новый тип мышления.

Все лучше осваивая искусство решения головоломок, мы не просто используем текущую ситуацию, чтобы узнать, какое правило нужно применить. Программа, основанная на порождающих правилах, делает похожее сопоставление с образцом. Это простое вычислительное мышление.

Когда мы записываем правила для создания программы, идет рука об руку с Мы скрываем подробности, касающиеся других частей головоломки, чтобы было легче продумывать, как шире обобщить правила. На схеме, иллюстрирующей наше последнее правило, мы использовали несколько абстракций, чтобы описать, как осуществлять Например, переменная — это Мы абстрагируемся от конкретного числа (то есть опускаем подробности) — правило применимо независимо от числа. Кроме того, мы используем знак вопроса в качестве другой переменной, чтобы абстрагироваться от конкретного положения четвертого шестиугольника в нашем представлении правила. Подобным образом мы абстрагируемся от ориентации схемы — ее можно как угодно вращать или отражать, но она будет соответствовать решаемой головоломке.

Оглавление книги