Книга: КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия
11.3. Сведение стереометрических задач к планиметрическим
11.3. Сведение стереометрических задач к планиметрическим
Основной способ решения стереометрических задач — сведение их к планиметрическим. Для этого можно применить метод проекций, заключающийся в проецировании геометрического объекта на подходящую плоскость. Преимуществом метода проекций является то, что он позволяет отобразить на плоском рисунке и увязать друг с другом элементы объектов, не лежащие в одной плоскости. При этом если объект расположить надлежащим образом по отношению к плоскости рисунка, то искомые метрические характеристики (и линейные, и угловые) проецируются на подходящую плоскость в заранее предусмотренном виде, например в натуральную величину.
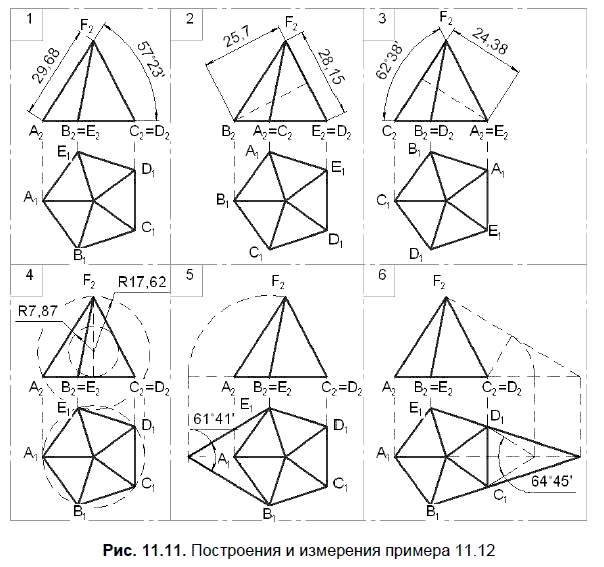
Пример 11.12
Условие. Дана правильная пятиугольная пирамида ABCDEF. Радиус окружности, описанной вокруг основания АВCDE, равен 16 мм. Высота пирамиды 25 мм. Определить следующие метрические характеристики:
? длину бокового ребра AF и угол его наклона к основанию;
? расстояние от вершины В до противоположной грани и высоту этой грани;
? угол между гранями с общим ребром AF и расстояние от этого ребра до ребра CF;
? диаметры вписанной в пирамиду и описанной вокруг пирамиды сфер;
? угол между ребрами BF и EF, соединяющими вершину пирамиды с противолежащими вершинами основания;
? угол между боковыми гранями Е = BCF и Q = DEF, не имеющими общего ребра.
Решение примера представлено на рис. 11.11.
- Глава 11 Решения планиметрических задач с помощью двумерного редактора
- 1.1. Информатика. Предмет информатики. Основные задачи информатики
- Повторяющиеся задачи
- Постановка задачи
- 24.1. Расширение возможностей Панели задач
- 2.5.3. Настройки панели задач и меню Пуск
- 1.1.1. Смысл, цель и задачи бизнес-тренинга
- Использование панели задач Управление документами в приложениях Office 2007
- Глава 3 Нормативные руководящие документы, назначение и задачи информационной безопасности России
- 4.1. Суть обзора задач в тайм-менеджменте. Основные понятия и определения
- 1.3. Задачи рекламного текста
- 2.4. Система постановки задач и управление проектами




