Книга: Размышления о думающих машинах. Тьюринг. Компьютерное исчисление

ИЗУЧЕНИЕ ПОДСОЛНУХОВ. НЕЗАКОНЧЕННЫЙ ОПЫТ ТЬЮРИНГА

Одной из последних работ Тьюринга стало изучение морфогенеза растений. В 2012 году на научном фестивале в Манчестере в рамках празднования столетия со дня рождения Тьюринга горожанам было предложено провести один опыт, который сам ученый оставил незаконченным. Его увлечение последовательностями чисел и моделями геометрических форм привело к мысли, что количество лепестков и расположение семян подсолнуха соответствуют последовательности Фибоначчи. Возможно, его вдохновила опубликованная в 1938 году работа Иоганнеса Шоуте, который изучал этот вопрос на 319 подсолнухах. К сожалению, этот и другие проекты были оставлены ученым после ареста в 1952 году и осуждения. Приведем описание его опыта, чтобы вы могли его воспроизвести. Сначала нужно посадить от одного до пяти семечек подсолнечника в необходимое количество горшков, расположить их в хорошо освещенном солнечном месте при температуре от 13 до 30 °С. Поливать семена нужно умеренно, не заливая их водой. Желательно проконсультироваться в магазине о том, какие сорта подсолнечника лучше растут в горшках. Например, красностебельный подсолнух является скорее декоративным видом, но есть еще такие, как «Гигантский», «Русский мамонт» или «Солнечный луч» — их изобразил Ван Гог на своей знаменитой картине. Когда придет время, подсчитаем спирали, по которым располагаются семена. Национальный музей математики в Нью-Йорке отмечает, что если подсчитывать спирали согласно инструкциям на веб-странице http://momath.org, то результат всегда будет последовательностью Фибоначчи (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...). Это последовательность, начинающаяся 0 и 1, а остальные числа в ней — результат сложения двух предыдущих (xn = x_n-1 + x_n-2). Наконец, и это самая удивительная часть опыта, если мы разделим один член последовательности Фибоначчи на предыдущий, например 55 на 34, в результате получим число, примерно равное золотому сечению (1,61803). Это число представляет собой канон красоты и гармонии в архитектуре и искусстве, но его можно обнаружить и в природе. Вычисляется золотое число по формуле ? = (1+?5)/2.

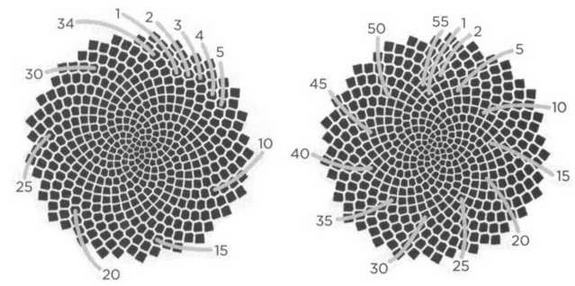
Спирали, по которым расположены семена подсолнечника, могут быть подсчитаны слева направо (схема слева) или наоборот (схема справа).

Одной из проблем, которые изучал ученый, была компьютерная симуляция морфогенеза, то есть роста и развития живых существ. Одним из любопытных экспериментов в данной теме стало применение к структуре растений последовательности Фибоначчи (ок. 1170 — ок. 1250). Эта последовательность (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...), обнаруженная итальянским математиком, получается при применении следующего алгоритма: если у нас 0 — первое число (a_t = 0), а 1 — второе (а₂ = 1), то другие числа последовательности, то есть an, образуются в результате сложения двух предшествующих чисел, следовательно an = a_n-1 + a_n-1. В мире растений данной последовательности соответствует количество лепестков и чашелистиков цветов и расположение чешуек ананаса. Почему же листья растений располагаются именно таким образом? Согласно экспериментальным данным, расположение листьев в соответствии с последовательностью Фибоначчи позволяет растению получать максимальное количество света.

Одна из важнейших работ Тьюринга была связана с изучением формирования полосок и пятен на шкуре позвоночных. Невероятно, но эти актуальнейшие исследования по морфогенезу ученый осуществлял с использованием нейронной цепи: он предположил, что между этими явлениями может быть связь. Также он пытался проанализировать, не является ли сама структура мозга и, следовательно, нейронных схем результатом контроля генов в ходе развития. Вопрос, поставленный Тьюрингом, звучал следующим образом: как формируются полоски и пятна на шкуре млекопитающих, рыб и поверхности моллюсков? В 1952 году Алан Тьюринг опубликовал статью «Химические основы морфогенеза», которую цитируют до сих пор. В ней была предложена гипотеза о том, что формирование, например, пятен далматинца или полосок зебры, основано на механизме реакции — диффузии.

Тьюринг считал, что у эмбрионов рисунок кожи имеет одинаковый вид и находится в стабильном состоянии, без пятен и полосок. Появление рисунка у эмбриона объясняется наличием клеток, производящих пигмент и ответственных за нарушение первоначального равновесия. Так возникают, например, характерные полоски у зебры. Эту окраску, обычную для взрослой особи, Тьюринг считал результатом нестабильного состояния организма. Он предположил следующий механизм: пигментные клетки образовывают два класса молекул, два разных типа морфогенов. Согласно определению самого Тьюринга, один тип (активаторный) способствует появлению рисунка, другой (ингибиторный) замедляет появление рисунка и нейтрализует активаторный морфоген. Два типа молекул распространяются по ткани эмбриона, взаимодействуя между собой, в результате получается определенный тип концентрации, или «след», который задает направление развития клеток эмбриона и, таким образом, формирует окрас взрослой особи. На основе этих рассуждений Тьюринг предложил уравнения реакции — диффузии, которые по сей день являются фундаментальными при изучении морфогенеза с помощью математики и компьютера. Работы по росту и развитию организмов стали последними в жизни Тьюринга.

В 2003 году чемпион мира по шахматам Гарри Каспаров сыграл четыре партии с шахматной программой Fritz, из которых две закончились вничью, а две оставшиеся выиграли по одному разу каждый из противников. На фотографии: Каспаров изучает движения на начальных минутах партии.

Дом в Уилмслоу (Чешир, Англия), где жил и покончил с собой Тьюринг.

Оглавление книги