Книга: Фундаментальные алгоритмы и структуры данных в Delphi

Массивы

Массивы

Предположим, что у нас имеется отсортированный массив. Как было показано ранее, алгоритм последовательного поиска даже при использовании выхода из цикла в случае отсутствия в списке искомого элемента принадлежит к классу O(n). Каким образом можно улучшить быстродействие?

Ответом может служить бинарный поиск. Он основан на стратегии "разделяй и властвуй": начинаем с большой проблемы, разбиваем ее на маленькие проблемы, которые легче решить, а, затем, следовательно, решаем всю большую проблему.

Бинарный поиск работает следующим образом. Берем средний элемент массива. Равен ли он искомому элементу? Если да, то поиск успешно завершен. В противном случае, если искомый элемент меньше среднего, то можно сказать, что, если элемент присутствует в массиве, он находится в первой половине. С другой стороны, если искомый элемент больше среднего, он должен находиться во второй половине. Таким образом, одним сравнением мы разбили нашу проблему на две части. Теперь мы применяем тот же алгоритм к выбранной части массива: находим средний элемент и определяем, в какой половине (точнее уже в четвертой части) находится искомый элемент. Мы снова делим проблему на две части. Описанные операции продолжаются до тех пор, пока искомый элемент не будет найден (разумеется, если он присутствует в массиве).

Это и есть алгоритм бинарного поиска. Поскольку размер массива при каждом выполнении цикла уменьшается в два раза, быстродействие алгоритма будет выражаться как O(log(n)), т.е. скорость работы алгоритма примерно пропорциональна функции двоичного логарифма log(_2_) от количества элементов в массиве (таким образом, возведение количества элементов массива во вторую степень приведет к увеличению времени поиска только в два раза).

Ниже приведен пример выполнения бинарного поиска в массиве TList (функцию можно найти в файле TDTList.pas на Web-сайте издательства, в разделе сопровождающих материалов).

Листинг 4.9. Бинарный поиск в отсортированном массиве TList

function TDTListSortedIndexOf(aList : TList; aItem : pointer;

aCompare : TtdCompareFunc) : integer;

var

L, R, M : integer;

CompareResult : integer;

begin

{задать значения для индексов первого и последнего элементов}

L := 0;

R := pred(aList.Count);

while (L <= R) do begin

{вычислить индекс среднего элемента}

M := (L + R) div 2;

{сравнить значение среднего элемента с искомым значением}

CompareResult := aCompare(aList.List^[M], aItem);

{если значение среднего элемента меньше искомого значения, переместить левый индекс на позицию до среднего индекса}

if (CompareResult < 0) then

L := succ(M)

{если значение среднего элемента больше искомого значения, переместить правый индекс на позицию после среднего индекса}

else if (CompareResult > 0) then

R := pred(M)

{в противном случае искомый элемент найден}

else begin

Result := M;

Exit;

end;

end;

Result := -1;

end;

Для описания подмассива, рассматриваемого в текущий момент, используются две переменных - L и R, которые хранят, соответственно, левый и правый индексы. Первоначально значения этих переменных устанавливаются равными 0 (первый элемент массива) и Count-1 (последний элемент массива). Затем мы входим в цикл While, из которого выйдем после обнаружения в массиве искомого элемента или когда значение переменной L превысит значение переменной R, что означает, что искомый элемент в массиве отсутствует. При каждом выполнении цикла вычисляется индекс среднего элемента (фактически это среднее значение между L и R). Затем значение элемента со средним индексом сравнивается с искомым значением. Если значение среднего элемента меньше, чем искомое, мы переносим левый индекс на позицию после среднего. В противном случае мы переносим правый индекс на позицию перед средним. Таким образом, мы определяем новый подмассив для поиска. Если же значение среднего элемента равно искомому, поиск завершен.

Для примера на рис. 4.1 приведены шаги, выполняемые при бинарном поиске буквы d в отсортированном массиве, содержащем буквы от a до k. На шаге (а) переменная L указывает на первый элемент (индекс 0), а R - на последний (индекс 10). Это означает, что значение переменной M будет составлять 5. Далее мы выполняем сравнение: значение элемента с индексом 5 равно f, а это больше искомого значения d.

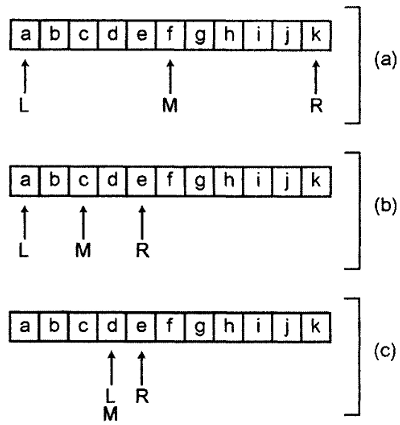
Рисунок 4.1. Бинарный поиск в массиве

Согласно алгоритму, мы устанавливаем значение R равным M-1 (таким образом, правая граница подмассива теперь находится слева от среднего элемента). Это означает, что значение R теперь равно 4. Новое значение среднего индекса будет равно 2, как показано на шаге (b). Выполняем сравнение: буква c (значение элемента с индексом 2) меньше, чем d.

Теперь, в соответствии с алгоритмом, необходимо установить индекс L за индексом M (т.е. M+1 или 3). Новое значение переменной M на шаге (с) равно 3. Выполняем сравнение: элемент с индексом 3 содержит букву d, а это и есть наше искомое значение. Поиск завершен.

Оглавление книги