Книга: Фундаментальные алгоритмы и структуры данных в Delphi

Вычисление LCS двух строк

Вычисление LCS двух строк

Требуемый нам алгоритм известен под названием алгоритма определения наиболее длинной общей подпоследовательности (longest common subsequence - LCS). Вначале мы рассмотрим, как он работает применительно к строкам, а затем расширим приобретенные представления на текстовые файлы.

Уверен, что все мы играли с детскими головоломками, в которых нужно было преобразовать одно слово в другое, изменяя по одной букве. Все промежуточные варианты должны были быть также осмысленными словами. Так, преобразуя слово CAT в слово DOG, можно было бы выполнить следующие преобразования: CAT, COT, COG, DOG.

Смысл этих игр со словами заключается в простом удалении на каждом шаге одной буквы и вставке новой. Если бы не ограничения, накладываемые правилами игры, можно было бы наверняка преобразовать одно слово в другое, просто удалив все старые символы и вставив вместо них новые. Такой метод решения задачи можно сравнить с применением кувалды, нам же весьма желательно найти несколько более тонкий подход.

Предположим, что наша цель заключается в отыскании наименьшего количества изменений, требуемых для преобразования одного слова в другое. Для примера преобразуем слово BEGIN в слово FINISH. Мы видим, что нужно удалить буквы В, Е и G, а затем вставить букву F перед оставшимися буквами и буквы I, S и H после них. Как же реализовать эти действия в виде алгоритма?

Один из возможных способов предполагает просмотр подпоследовательностей букв каждого слова и выяснение наличия в них общих последовательностей. Подпоследовательность (subsequence) строки образуется за счет удаления из нее одного или более символов. Оставшиеся символы не должны переставляться. Например, четырехбуквенными подпоследовательностями для строки BEGIN являются EGIN, BGIN, BEGIN, BEIN и BEGI. Как видите, они образуются путем поочередного отбрасывания одного из символов. Трехбуквенными подпоследовательностями являются BEG, BEI, BEN, BGI, BGN, BIN, EGI, EGN, EIN и GIN. Для данного слова существует 10 двухбуквенных подпоследовательностей и пять одно-буквенных. Таким образом, для пятибуквенного слова существует всего 30 возможных подпоследовательностей, а в общем случае можно было бы показать, что для n-буквенной последовательности существует около 2(^n^) подпоследовательностей. Пока что примите это утверждение на веру.

Алгоритм с применением "грубой силы", если его можно так назвать, заключается в просмотре двух слов BEGIN и FINISH и просмотре их пятибуквенных подпоследовательностей на предмет наличия каких-либо совпадений. Такие совпадения отсутствуют, поэтому для каждого слова то же самое нужно сделать, используя четырехбуквенные подпоследовательности. Как и в предыдущем случае, ни одна из подпоследовательностей не совпадает, поэтому мы переходим к рассмотрению трехбуквенных последовательностей. Результат снова отрицателен, поэтому мы переходим к сравнению двухбуквенных подпоследовательностей. Самой длинной общей подпоследовательностью этих двух слов является IN. Исходя из этого, можно определить, какие буквы необходимо удалить, а какие вставить.

Для коротких слов, подобных приведенному примеру, описанный подход не так уж плох. Но представим, что требуется просмотреть все подпоследовательности 100-символьной строки. Как уже упоминалось, их количество составляет 2(^100^). Алгоритм с применением "грубой силы" является экспоненциальным. Количество выполняемых операций пропорционально O(2(^n^)). Даже для строк средней длины поле поиска увеличивается чрезвычайно быстро. А это влечет за собой радикальное увеличение времени, требуемого для отыскания решения. Чтобы сказанное было нагляднее, представим следующую ситуацию: предположим, что можно генерировать около биллиона подпоследовательностей в секунду.(т.е. 2(^40^)= 1 099 511 627 776, или тысячу подпоследовательностей за один такт работы процессора ПК, тактовая частота которого равна 1 ГГц). Год содержит около 2(^25^) секунд. Следовательно, для генерации всего набора подпоследовательностей для 100-символьного слова потребовалось бы 2(^35^) (34 359 738 368) лет - 11-значное число. А теперь вспомните, что 100-символьная строка - всего лишь простенький пример того, что необходимо сделать: например, найти различие между двумя вариантами 600-строчного исходного файла.

Однако идея применения подпоследовательностей обладает своими достоинствами. Просто нужно подойти к ней с другой стороны. Вместо перечисления и сравнения всех подпоследовательностей в двух словах посмотрим, нельзя ли применить пошаговый подход.

Для начала предположим, что нам удалось найти наиболее длинную общую подпоследовательность двух слов (далее для ее обозначения мы будем использовать аббревиатуру "LCS"). В этом случае можно было бы соединить линиями буквы в LCS первого слова с буквами LCS второго слова. Эти линии не будут пересекаться. (Это обусловлено тем, что подпоследовательности определены так, что перестановки букв не допускаются. Поэтому буквы в LCS в обоих словах будут располагаться в одинаковом порядке.) LCS для слов "banana" и "abracadabra" (т.е. b, а, а, а) и линии, соединяющие совпадающие в них буквы, показаны на рис. 12.1. Обратите внимание, что для этой пары слов существует несколько возможных LCS. На рисунке, показана лишь первая из них (занимающая самую левую позицию).

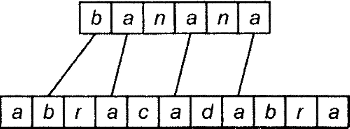
Рисунок 12.1. LCS для слов "banana" и "abracadabra"

Итак, тем или иным способом мы определили LCS двух слов. Предположим, что длина этой подпоследовательности равна х. Взгляните на последние буквы обоих слов. Если ни одна из них не является частью соединительной линии, и при этом они являются одной и той же буквой, то эта буква должна быть последней буквой LCS и между ними должна была бы существовать соединительная линия. (Если эта буква не является последней буквой подпоследовательности, ее можно было бы добавить, удлинив LCS на одну букву, что противоречило бы сделанному предположению о том, что первая подпоследовательность является самой длинной.) Удалим эту последнюю букву из обоих слов и из подпоследовательности.

Полученная сокращенная подпоследовательность длиной x - 1 представляет собой LCS двух сокращенных слов. (Если бы это было не так, для двух сокращенных слов должна была бы существовать общая подпоследовательность длиной X или больше. Добавление заключительных букв привело бы к увеличению длины новой общей подпоследовательности на единицу, а, значит, для двух полных слов должна была бы существовать общая подпоследовательность, содержащая x+1 или более букв. Это противоречит предположению о том, что мы определили LCS.)

Теперь предположим, что последняя буква в LCS не совпадает с последней буквой первого слова. Это означало бы, что LCS двух полных слов была бы также LCS первого слова без последней буквы и второго слова (если бы это было не так, можно было бы снова добавить последнюю букву к первому слову и найти более длинную LCS двух слов). Эти же рассуждения применимы и к случаю, когда последняя буква второго слова не совпадает с последней буквой LCS.

Все это замечательно, но о чем же оно свидетельствует? LCS содержит в себе LCS усеченных частей обоих слов. Для отыскания LCS строк X и Y мы разбиваем задачу на более мелкие задачи. Если бы последние символы слов X и Y совпадали, нам пришлось бы найти LCS для строк X и Y без их последних букв, а затем добавить эту общую букву. Если нет, нужно было бы найти LCS для строки X без последней буквы и строки Y, а также LCS строки X и строки Y без ее последней буквы, а затем выбрать более длинную из них. Мы получаем простой рекурсивный алгоритм.

Однако во избежание проблемы, которая может быть порождена простым решением, вначале необходимо описать алгоритм несколько подробней.

Мы пытаемся вычислить LCS двух строк X и Y. Вначале мы определяем, что строка X содержит n символов, а строка Y - m. Обозначим строку, образованную первыми i символами строки X, как Х(_i_). i может принимать также нулевое значение, что означает пустую стоку (это соглашение упростит понимание алгоритма). В таком случае Х(_n_) соответствует всей строке. С применением этой формы записи алгоритм сводится к следующему; если последние два символа строк Х(_n_) и Y(_m_) совпадают, самая длинная общая последовательность равна LCS Х(_n-1_) и Y(_m-1_) с добавлением этого последнего символа. Если они не совпадают, LCS равна более длинной из LCS строк Х(_n-2_) и Y(_m_) и LCS строк Х(_n_) и Y(_m-1_). Для вычисления этих "меньших" LCS мы рекурсивно вызываем одну и ту же подпрограмму.

Тем не менее, обратите внимание, что для вычисления LCS строк Х(_n-1_) и Y(_m_) может потребоваться вычислить LCS строк Х(_n-2_) и Y(_m-1_), LCS строк Х(_n-1_) и Y(_m-1_) и LCS строк Х(_n-2_) и Y(_m_). Вторую из этих подпоследовательностей можно уже вычислить. При недостаточной внимательности можно было бы вычислять одни и те же LCS снова и снова. В идеале во избежание этих повторных вычислений нужно было бы кешировать ранее вычисленные результаты. Поскольку мы располагаем двумя индексами для строк X и Y, имеет смысл воспользоваться матрицей.

Что необходимо хранить в каждом из элементов этого матричного кеша? Очевидный ответ - саму строку LCS. Однако, это не слишком целесообразно - да, это упростит вычисление LCS, но не поможет определить, какие символы нужно удалить из строки X, а какие новые символы вставить с целью получения строки Y. Лучше в каждом элементе хранить достаточный объем информации, чтобы можно было генерировать LCS за счет применения алгоритма типа O(1), а также достаточный объем информации для определения команд редактирования, обеспечивающих переход от строки X к строке Y.

Один из информационных элементов, в котором мы действительно нуждаемся, -это длина LCS на каждом этапе. Используя упомянутое значение, с помощью рекурсивного алгоритма можно легко выяснить длину LCS для двух полных строк. Чтобы можно было сгенерировать саму строку LCS, необходимо знать путь, пройденный по матричному кешу. Для этого в каждом элементе потребуется сохранять указатель на предыдущий элемент, который был использован для построения LCS для данного элемента.

Однако прежде чем приступить к рассмотрению просмотра матрицы LCS, необходимо ее построить. Пока же будем считать, что в каждом элементе матрицы будут храниться два информационных фрагмента: длина LCS на данном этапе и позиция предыдущего элемента матрицы, образующего предшественницу этой LCS. Для последнего значения существует только три возможных ячейки: непосредственно над ним (к северу), слева (к западу) и выше и левее (к северо-западу). Поэтому для их обозначения вполне можно было бы использовать перечислимый тип.

Давайте вручную вычислим LCS для случая строк BEGIN/FINISH. Мы получим матрицу 6x7 (мы будем учитывать пустые подстроки, поэтому индексация должна начинаться с 0). Вместо того, чтобы рекурсивно заполнять матрицу (все эти рекурсивные вызовы трудно поддерживать в упорядоченном виде), итеративно вычислим все ячейки слева направо и сверху вниз. Вычисление ячеек первой строки и первого столбца не представляет сложности: они все являются нулями. Почему? Да потому, что наиболее длинная общая последовательность пустой и любой другой строки равна нулевой строке. С этого момента можно начать определение LCS для ячейки (1,1) или двух строк B и F. Два последних символа этих односимвольных строк не совпадают. Следовательно, длина LCS равна максимальной из предшествующих ячеек, расположенных к северу и к западу от данной. Обе эти ячейки нулевые, поэтому их максимальное значение и, следовательно, значение этой ячейки равно нулю. Ячейка (1,2) соответствует строкам B и F1. Ее значение также рано нулю. Ячейка (2,1) соответствует строкам BE и F: длина LCS снова равна 0. Продолжая подобные вычисления, можно заполнить все 42 ячейки матрицы. Обратите внимание на ячейки, соответствующие совпадающим символам: именно в них длина LCS возрастает. Конечный результат показан в таблице 12.1.

Таблица 12.1. Матрица LCS для строк BEGIN и FINISH

_ _ F I N I S H

_ 0 0 0 0 0 0 0

B 0 0 0 0 0 0 0

E 0 0 0 0 0 0 0

G 0 0 0 0 0 0 0

I 0 0 1 1 1 1 1

N 0 0 1 2 2 2 2

Записать этот процесс выполнения действий вручную в виде кода не особенно трудно. Чтобы облегчить задачу начинающим программистам, я решил вначале создать класс матричного кеша. Внутри этого класса матрица хранится в объекте TList из TLists, причем ведущий объект TList представляет строки в матрице, а ведомый TLists - ячейки в столбцах отдельной строки. Кроме того, класс матрицы специфичен для решаемой задачи. Было бы излишним разрабатывать, кодировать и использовать общий класс матрицы. Код реализации класса матрицы показан в листинге 12.22.

Листинг 12.22. Класс матрицы для реализации алгоритма определения LCS

type

TtdLCSDir = (ldNorth, ldNorthWest, ldWest);

PtdLCSData = ^TtdLCSData;

TtdLCSData = packed record

ldLen : integer;

ldPrev : TtdLCSDir;

end;

type

TtdLCSMatrix = class private

FCols : integer;

FMatrix : TList;

FRows : integer;

protected

function mxGetItem(aRow, aCol : integer): PtdLCSData;

procedure mxSetItem(aRow, aCol : integer;

aValue : PtdLCSData);

public

constructor Create(aRowCount, aColCount : integer);

destructor Destroy; override;

procedure Clear;

property Items [aRow, aCol : integer] : PtdLCSData

read mxGetItem write mxSetItem;

default;

property RowCount : integer read FRows;

property ColCount : integer read FCols;

end;

constructor TtdLCSMatrix.Create(aRowCount, aColCount : integer);

var

Row : integer;

ColList : TList;

begin

{создать производный объект}

inherited Create;

{выполнить простую проверку}

Assert ((aRowCount > 0) and (aColCount > 0),

' TtdLCSMatrix.Create: Invalid Row or column count');

FRows := aRowCount;

FCols := aColCount;

{создать матрицу: она будет матрицей TList матриц TLists, упорядоченных по строкам}

FMatrix := TList.Create;

FMatrix.Count := aRowCount;

for Row := 0 to pred(aRowCount) do

begin

ColList := TList.Create;

ColList.Count := aColCount;

TList(FMatrix.List^[Row]) := ColList;

end;

end;

destructor TtdLCSMatrix.Destroy;

var

Row : integer;

begin

{уничтожить матрицу}

if (matrix <> nil) then begin

Clear;

for Row := 0 to pred(FRows) do

TList(FMatrix.List^[Row]).Free;

FMatrix.Free;

end;

{уничтожить производный объект}

inherited Destroy;

end;

procedure TtdLCSMatrix.Clear;

var

Row, Col : integer;

ColList : TList;

begin

for Row := 0 to pred(FRows) do

begin

ColList := TList(FMatrix.List^[Row]);

if (ColList <> nil) then

for Col := 0 to pred(FCols) do

begin

if (ColList.List^[Col] <> nil) then

Dispose(PtdLCSData(ColList.List^[Col]));

ColList.List^[Col] :=nil;

end;

end;

end;

function TtdLCSMatrix.mxGetItem(aRow, aCol : integer): PtdLCSData;

begin

if not ((0 <= aRow) and (aRow < RowCount) and (0 <= aCol) and (aCol < ColCount)) then

raise Exception.Create(

'TtdLCSMatrix.mxGetItem: Row or column index out of bounds');

Result := PtdLCSData(TList(FMatrix.List^[aRow]).List^[aCol]);

end;

procedure TtdLCSMatrix.mxSetItem(aRow, aCol : integer;

aValue : PtdLCSData);

begin

if not ((0 <= aRow) and (aRow < RowCount) and (0 <= aCol) and (aCol < ColCount)) then

raise Exception.Create(

'TtdLCSMatrix.mxSetItem: Row or column index out of bounds');

TList(Matrix.List^[aRow]).List^[aCol] := aValue;

end;

Следующий шаг заключается в создании класса, который реализует алгоритм вычисления LCS для строк. Код интерфейса и выполнения служебных функций класса TtdStringLCS приведен в листинге 12.23.

Листинг 12.23. Класс TtdStringLCS

type

TtdStringLCS = class private

FFromStr : string;

FMatrix : TtdLCSMatrix;

FToStr : string;

protected

procedure slFillMatrix;

function slGetCell(aFromInx, aToInx : integer): integer;

procedure slWriteChange(var F : System.Text;

aFromInx, aToInx : integer);

public

constructor Create(const aFromStr, aToStr : string);

destructor Destroy; override;

procedure WriteChanges(const aFileName : string;

end;

constructor TtdStringLCS.Create(const aFromStr, aToStr : string);

begin

{создать производный объект}

inherited Create;

{сохранить строки}

FFromStr := aFromStr;

FToStr :=aToStr;

{создать матрицу}

FMatrix := TtdLCSMatrix.Create(succ(length(aFromStr)), succ(length(aToStr)));

{заполнить матрицу}

slFillMatrix;

end;

destructor TtdStringLCS.Destroy;

begin

{уничтожить матрицу}

FMatrix.Free;

{уничтожить производный объект}

inherited Destroy;

end;

При первой реализации алгоритма вычисления LCS я столкнулся с дилеммой: придерживаться ли ранее описанного рекурсивного алгоритма или же только что описанного процесса вычисления LCS вручную? Чтобы получить ответ на ряд вопросов (какой из методов проще, какой требует использования меньшего объема памяти, какой работает быстрее), я реализовал оба подхода, причем начал с реализации итеративного метода. Это итеративное решение приведено в листинге 12.24.

Листинг 12.24. Итеративное вычисление LCS

procedure TtdStringLCS.slFillMatrix;

var

FromInx : integer;

ToInx : integer;

NorthLen: integer;

WestLen : integer;

LCSData : PtdLCSData;

begin

{создать пустые элементы, располагающиеся вдоль верхней и левой сторон матрицы}

for ToInx := 0 to length (FToStr) do

begin

New(LCSData);

LCSData^.ldLen := 0;

LCSData^.ldPrev := ldWest;

FMatrix[0, ToInx] := LCSData;

end;

for FromInx := 1 to length (FFromStr) do

begin

New(LCSData);

LCSData^.ldLen := 0;

LCSData^.ldPrev := ldNorth;

FMatrix [FromInx, 0] := LCSData;

end;

{построчное, слева направо, заполнение матрицы}

for FromInx := 1 to length (FFromStr) do

begin

for ToInx := 1 to length (FToStr) do

begin {создать новый элемент}

New(LCSData);

{если два текущих символа совпадают, необходимо увеличить значение счетчика элемента, расположенного к северо-западу, т.е. предыдущего элемента}

if (FFromStr[FromInx] = FToStr[ToInx]) then begin

LCSData^.ldPrev := ldNorthWest;

LCSData^.ldLen := succ(FMatrix[FromInx-1, ToInx-1]^.ldLen);

end

{в противном случае текущие символы различны: необходимо использовать максимальный из элементов, расположенных к северу или к западу от текущего (к западу предпочтительнее)}

else begin

NorthLen := FMatrix[FromInx-1, ToInx]^.ldLen;

WestLen := FMatrix[FromInx, ToInx-1]^.ldLen;

if (NorthLen > WestLen) then begin

LCSData^.ldPrev := ldNorth;

LCSData^.ldLen := NorthLen;

end

else begin

LCSData^.ldPrev :=ldWest;

LCSData^.ldLen := WestLen;

end;

end;

{установить элемент в матрице}

FMatrix[FromInx, ToInx] := LCSData;

end;

end;

{на этом этапе длина элемента, расположенного в нижнем правом углу, равна LCS, и вычисление завершено}

end;

Мы начинаем с заполнения верхней строки и левого столбца матрицы нулевыми ячейками. Длина LCS в этих ячейках равна нулю (вспомните, что они описывают LCS пустой и какой-либо другой строки), и мы всего лишь устанавливаем флаг направления, дабы он указывал на предшествующую ячейку, ближайшую к ячейке (0,0). Затем следует вложенный цикл (цикл по столбцам внутри цикла по строкам). Для каждой строки мы вычисляем LCS для каждой из ячеек,.просматривая их слева направо. Эти вычисления выполняются для всех строк сверху вниз. Вначале мы проверяем, совпадают ли два символа, на которые ссылается ячейка. (Ячейка матрицы представляет собой переход от символа строки From (Из) к символу строки То (В).) Если они совпадают, длина LCS в этой ячейке равна длине LCS ячейки, расположенной к северо-западу от данной, плюс единица. Обратите внимание, что способ вычисления ячеек предполагает, что ячейка, на которую осуществляется ссылка, уже вычислена (именно поэтому мы заранее вычислили значения ячеек, расположенных вдоль верхней и левой сторон матрицы). Если два символа не совпадают, необходимо просмотреть ячейки, расположенные к северу и к западу от текущей. Мы выбираем ту, которая содержит наиболее длинную LCS, и используем это значение в качестве значения данной ячейки. Если две длины равны, можно выбрать любую из них. Однако мы будем придерживаться правила, что предпочтительнее выбирать LCS, соответствующую ячейке, которая расположена слева. Этот выбор обусловлен тем, что как только путь через матрицу, обеспечивающий определение LCS обеих строк, вычислен, удаления из первой строки выполняются раньше вставок во вторую строку.

Обратите внимание, что приведенный в листинге 12.24 метод требует постоянного времени для обработки двух строк, независимо от степени их совпадения или несовпадения. Если длина строк равна, соответственно, n и т, то время, требуемое для выполнения основного цикла, будет пропорционально произведению n * m, поскольку таковым является количество ячеек, значения которых нужно вычислить. (помните, что ячейка, для которой действительно нужно получить ответ - последняя, значение которой должно вычисляться;

она расположена в нижнем правом углу матрицы).

Алгоритм, реализованный с применением рекурсивного метода, приведен в листинге 12.25. Рекурсивная подпрограмма кодируется в виде функции, которая возвращает длину LCS для конкретной ячейки, заданной индексом строки и столбца (которые, в конечном счете, представляют собой индексы, указывающие на строки From и То).

Листинг 12.25. Рекурсивное вычисление LCS

function TtdStringLCS.slGetCell(aFromInx, aToInx : integer): integer;

var

LCSData : PtdLCSData;

NorthLen: integer;

WestLen : integer;

begin

if (aFromInx = 0) or (aToInx = 0) then

Result := 0

else begin

LCSData := FMatrix[ aFromInx, aToInx];

if (LCSData <> nil) then

Result := LCSData^.ldLen else begin

{создать новый элемент}

New(LCSData);

{если два символа совпадают, необходимо увеличить значение счетчика относительно элемента, расположенного к северо-западу от данного, т.е. предшествующего элемента}

if (FFromStr[aFromInx] = FToStr [aToInx]) then begin

LCSData^.ldPrev := ldNorthWest;

LCSData^.ldLen := slGetCell(aFromInx-1, aToInx-1) + 1;

end

{в противном случае текущие символы различаются: необходимо использовать максимальный из элементов, расположенных к северу и западу (выбор элемента расположенного к западу предпочтительнее)}

else begin

NorthLen := slGetCell(aFromInx-1, aToInx);

WestLen := slGetCell(aFromInx, aToInx-1);

if (NorthLen > WestLen) then begin

LCSData^.ldPrev := ldNorth;

LCSData^.ldLen := NorthLen;

end

else begin

LCSData^.ldPrev := ldWest;

LCSData^.ldLen := WestLen;

end;

end;

{установить значение элемента матрицы}

FMatrix[aFromInx, aToInx] := LCSData;

{вернуть длину данной LCS}

Result := LCSData^.ldLen;

end;

end;

end;

Первое существенное различие состоит в том, что не нужно генерировать нулевые значения для ячеек, расположенных вдоль верхней и правой сторон матрицы. Теперь эту задачу выполняет простой оператор If. (Честно говоря, в итеративном варианте вычисления LCS можно было бы обойтись без вычисления этих значений, но в этом случае внутренний код цикла оказался бы значительно сложнее для понимания и поддержки. Поэтому для простоты мы заранее вычисляем значения этих ячеек.) Если значение ячейки уже вычислено, мы просто возвращаем ее длину LCS. Если нет, необходимо выполнить ту же проверку, что и в предыдущем случае: совпадают ли два символа? Если да, то необходимо добавить единицу к значению LCS ячейки, расположенной к северо-западу от данной. Если нет, необходимо использовать большее из значений длины LCS ячеек, расположенных к северу и к западу от текущей. Естественно, эти значения LCS вычисляются в результате рекурсивных вызовов этой подпрограммы.

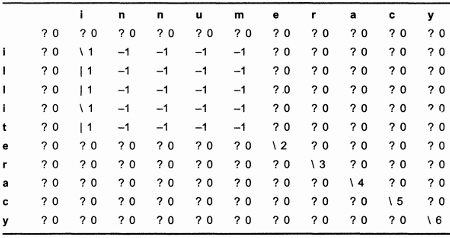
Применив обе версии (итеративную и рекурсивную), я сгенерировал матрицу для вычисления LCS слов "illiteracy" и "innumeracy". (Длина LCS этих слов равна 6 и выглядит как "ieracy".) Результаты этих немалых трудов приведены в таблицах 12.2 и 12.3. При использовании рекурсивной версии многие ячейки вообще не вычисляются (они помечены знаком вопроса). Эти ячейки образуют часть заключительной LCS.

Таблица 12.2. Итеративная матрица LCS слов "illiteracy" и "innumeracy".

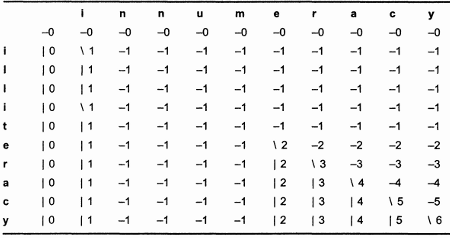
Таблица 12.3. Рекурсивная матрица LCS слов "illiteracy" и "innumeracy".

Итак, мы получили матрицу, которая определяет наиболее длинную общую подпоследовательность. Как ее можно использовать? Одна возможность связана с реализацией подпрограммы, которая создает текстовый файл, описывающий изменения, называемые последовательностью редактирования (edit sequence). Это может упростить создание аналогичной подпрограммы для текстового файла - что, собственно, является конечной целью данного раздела.

Код реализации простой технологии обхода, которая может быть приведена в соответствие с нашими потребностями, показан в листинге 12.26. Подпрограмма содержит два метода: первый вызывается пользователем с указанием имени файла, а второй представляет собой рекурсивную подпрограмму, которая записывает данные в файл. Весь основной объем работы выполняется во второй подпрограмме. Поскольку в матрице путь LCS кодируется в обратном направлении (т.е. для определения пути необходимо начать с конца и продвигаться к началу матрицы), мы создаем метод, который вначале вызывает сам себя, а затем записывает данные, соответствующие текущей позиции. Необходимо обеспечить прерывание выполнения рекурсивной подпрограммы. Это соответствует случаю, когда подпрограмма вызывается для ячейки (0,0). В этом случае никакие данные не записываются в файл. Если индекс строки То равен нулю, мы выполняем рекурсивный вызов, перемещаясь вверх по матрице (индекс строки From уменьшается), и предпринимаемым действием должно быть удаление символа из строки From. Если индекс строки From равен нулю, мы выполняем рекурсивный вызов, перемещаясь по матрице влево, и тогда действием является ставка текущего символа в строку То. И, наконец, если оба индекса не равны нулю, мы находим соответствующую ячейку в матрице, выполняем рекурсивный вызов и записываем действие в файл. Перемещению вниз соответствует удаление, перемещению вправо - вставка, перемещению по диагонали - ни одно из упомянутых действий (символ "переносится" из одной строки в другую). Для обозначения удаления мы будем использовать стрелку, указывающую вправо (-> ), а для обозначения вставки - стрелку, указывающую влево (<-). Перенос символа не обозначается.

Листинг 12.26. Вывод последовательности редактирования

procedure TtdStringLCS.slWriteChange(var F : System.Text;

aFromInx, aToInx : integer);

var

Cell : PtdLCSData;

begin

{если оба индекса равны нулю, данная ячейка является первой ячейкой матрицы LCS, поэтому подпрограмма просто выполняет выход}

if (aFromInx = 0) and (aToInx = 0) then

Exit;

{если индекс строки From равен нулю, ячейка расположена в левом столбце матрицы, поэтому необходимо переместиться вверх; этому будет соответствовать удаление}

if (aFromInx = 0) then begin

slWriteChange(F, aFromInx, aToInx-1);

writeln(F, '->', FToStr[aToInx]);

end

{если индекс строки To равен нулю, ячейка расположена в верхней строке матрицы, поэтому необходимо переместиться влево; этому будет соответствовать вставка}

else

if (aToInx = 0) then begin

slWriteChange(F, aFromInx-1, aToInx);

writeln(F, '< - FFromStr[aFromInx]);

end

{в противном случае необходимо выполнить действия, указанные ячейкой}

else begin

Cell := FMatrix[aFromInx, aToInx];

case Cell^.ldPrev of

ldNorth : begin

slWriteChange(F, aFromInx-1, aToInx);

writeln(F, ' <- ', FFromStr[aFromInx]);

end;

ldNorthWest : begin

slWriteChange(F, aFromInx-1, aToInx-1);

writeln(F, ' ', FFromStr[aFromInx]);

end;

ldWest : begin

slWriteChange(F, aFromInx, aToInx-1);

writeln(F, '-> FToStr[aToInx]);

end;

end;

end;

end;

procedure TtdStringLCS.WriteChanges(const aFileName : string);

var

F : System.Text;

begin

System.Assign(F, aFileName);

System.Rewrite(F);

try

slWriteChange(F, length(FFromStr), length(FToStr));

finally

System.Close(F);

end;

end;

Ниже показан текстовый файл, который был сгенерирован для преобразования слова "illiteracy" в слово "innumeracy".

< - i

<- l

<- l

i

<- t

-> n

-> n

-> u

-> m

e

r

a

с

y

Это представление действий по редактированию легко доступно для понимания, но при необходимости его можно развернуть. Как видите, наиболее длинная общая подпоследовательностью является (i, e, r, a, c, y), а определение удалений и вставок не представляет сложности.

Памятуя о том, что примененный метод является рекурсивным, следует подумать о требуемой для его реализации глубине стека. Если бы строки вообще не имели общих символов, последовательность редактирования сводилась бы к удалению всех символов первой строки и вставке всех символов второй строки. Если первая строка содержит n символов, а вторая m, глубина стека должна быть пропорциональной сумме n + m.

Оглавление книги