Книга: Феномен науки. Кибернетический подход к эволюции

10.7. В поисках аксиом

10.7. В поисках аксиом

Для понимания природы математической достоверности очень поучительно довести до конца разбор утверждения E₁. Поскольку у нас все-таки остались некоторые сомнения относительно абсолютной необходимости пересечения окружности на рис. 10.3, попробуем представить себе ситуацию, когда они не пересекаются. Полная неудача этой попытки будет означать, что утверждение E₁ математически достоверно и не может быть разложено на более простые утверждения; тогда его следует принять в качестве аксиомы. Если же нам ценой большего или меньшего насилия над воображением удастся представить себе ситуацию, в которой ?_A и ?_B не пересекаются, эта ситуация, надо полагать, придет в противоречие с какими-то более простыми и глубокими утверждениями, обладающими математической достоверностью; тогда мы их и примем за аксиомы, а наличие противоречия будет служить доказательством E₁. Таков обычный путь к установлению аксиом в математике.

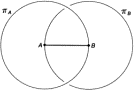
Рис. 10.4. «Перескакивающие» окружности

Оглавление книги