Книга: Феномен науки. Кибернетический подход к эволюции

9.4. Позиционная система

9.4. Позиционная система

Основы позиционной системы заложили вавилоняне. В системе счисления, которую они заимствовали от своих предшественников — шумерийцев, мы с самого начала (т. е. в древнейших дошедших до нас глиняных табличках, относящихся к началу третьего тысячелетия до н. э.), видим две основные «большие единицы» — десять и шестьдесят. Откуда взялось число шестьдесят — об этом можно только догадываться. Известный историк математики О. Нейгебауэр полагает, что источником послужило отношение между основными денежными единицами, имевшими хождение в Двуречье: одна мана (по гречески мина) составляла шестьдесят шекелей. Такое объяснение не удовлетворяет нашего любопытства, ибо тотчас же возникает вопрос: а почему в мане шестьдесят шекелей? Не потому ли как раз, что в ходу была шестидесятиричная система? Ведь не потому мы считаем десятками и сотнями, что в рубле сто копеек! Ассириолог Ф. Тюро-Данжен приводит лингвистические аргументы в пользу того, что система счета была первичным явлением, а система мер — вторичным. Выбор числа шестьдесят был, очевидно, исторической случайностью, однако вряд ли можно усомниться, что этой случайности способствовала важная особенность числа шестьдесят: оно имеет необычайно много делителей: 2, 3, 4, 5, 6, 10, 12, 15, 20, 30. Это свойство очень полезно и для денежной единицы (с тех пор как существуют деньги, существует и деление их поровну), и для основания системы счета, если предположить, что какой-то мудрец ввел ее, руководствуясь соображениями удобства вычислений.

Математическая культура вавилонян известна нам по текстам, относящимся к двум периодам: древневавилонскому (1800–1600 гг. до н. э.) и эпохе Селевкидов (305–64 гг. до н. э.). Сравнение их показывает, что в математике вавилонян каких-либо радикальных перемен за эти полтора тысячелетия не произошло.

Вавилоняне изображали единицу узким вертикальным клинышком

, а десять — широким горизонтальным
. Число 35 выглядело так:
. Аналогично изображались числа до 59 включительно. Но 60 изображалось снова узким вертикальным клинышком, таким же, как единица! На самых древних табличках можно видеть, что клинышек, изображающий 60, больше, чем клинышек единицы. Таким образом, число 60 не только понималось как «большая единица», но и изображалось, в буквальном смысле слова, как большая единица. Соответственно появились «большие десятки» для десятикратно увеличенных больших единиц. Затем различие между большими и маленькими клиньями стерлось, они стали распознаваться по своему положению. Так возникла позиционная система. Число 747 = 12 ? 60 + 27 вавилонянин записал бы в виде:
. Числу 60² = 3600 соответствует третий шестидесятиричный разряд и т. д. Но самое замечательное, что таким же образом вавилоняне изображали и дроби. В числе, следовавшем за числом единиц, каждая единица обозначала ¹/₆₀, в следующем за ним числе — ¹/₃₆₀₀ и т. д. В современной десятичной записи мы отделяем целую часть от дробной точкой или запятой. Чем же отделяли целую часть от дробной вавилоняне? Ничем! Число
могло с равным успехом обозначать и полтора и девяносто. Та же неопределенность имела место и в записи целых чисел: числа n, n ? 60, n ? 60² и т. д. были неотличимы. Множители или делители, кратные шестидесяти, надо было добавлять по смыслу. Так как 60 — довольно большое число, это к особенным неприятностям не приводило.

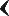
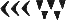
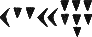
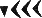
Сравнивая вавилонскую позиционную систему с современной, мы видим, что неопределенность в множителе 60 — результат отсутствия знака нуль, который мы приписали бы нужное число раз в конце целого числа или начале дробного. Другим результатом отсутствия нуля является еще более серьезная неопределенность в интерпретации числовой записи, которая соответствует тому случаю, когда мы ставим нули в промежуточных разрядах. В самом деле, как отличить в вавилонской записи число 3601 = 1 ? 60² + 0 ? 60 + 1 от числа 61 = 1 ? 60 + 1? Оба эти числа изображаются двумя единицами. Иногда неопределенность такого рода устранялась путем отодвижения чисел друг от друга с оставлением свободного места для недостающего разряда. Но этот метод не применялся систематически и во многих случаях большой пробел между числами ничего не означал. В астрономических таблицах эпохи Селевкидов встречается обозначение отсутствующего разряда с помощью знака, аналогичного нашей точке (разделитель фраз). В древневавилонскую эпоху ничего подобного мы не находим. Как же умудрялись древние вавилоняне избегать путаницы?

Полагают¹, что разгадка состоит в следующем.

Ранние математические тексты вавилонян, дошедшие до нас, представляют собой сборники задач и их решений, созданные несомненно как учебные пособия. Их цель — обучить практическим приемам решения задач. Но ни в одном из текстов не описывается, как производить арифметические действия, в частности такие сложные для своего времени, как умножение и деление. Следовательно, предполагалось, что ученики каким-то образом умеют это делать. Так как совершенно невероятно, чтобы вычисления производились в уме, естественно предположить, что вавилоняне пользовались каким-то счетным прибором типа абака. На абаке числа выступают в своем натуральном, стихийно позиционном виде, а специальный знак для нуля не нужен, ибо бороздка, соответствующая пустому разряду, просто остается без камешков. Представление числа на абаке было основной формой задания числа, и в этом представлении не было никакой неопределенности. Числа, которые приводятся в клинописных математических текстах, играют роль поэтапных ответов, призванных контролировать правильность хода решения. Ученик делал выкладки на абаке и сверялся с глиняной табличкой. Ясно, что такому контролю отсутствие знака для пустых разрядов нисколько не препятствовало. Когда распространились объемистые астрономические таблицы, служащие уже не для контроля, а в качестве единственного источника данных, стали употреблять и разделительный знак для обозначения пустых разрядов. Однако свой «нуль» вавилоняне никогда не ставили в конце числа: очевидно, они его воспринимали именно как разделитель, но не как полноправное число.

Познакомившись с египетской и вавилонской системами записи дробей и действий над ними, греки для астрономических вычислений выбрали вавилонскую, ибо она была несравненно лучше. Но в записи целых чисел они сохранили свою алфавитную систему. Таким образом, греческая система, употреблявшаяся в астрономии, оказалась смешанной: целая часть числа изображалась в десятичной непозиционной системе, дробная часть — шестидесятиричной позиционной.

Не слишком логичное решение для создателей логики! С их легкой руки мы и до сих пор считаем часы и градусы (угловые) десятками и сотнями, а делим их на минуты и секунды.

Зато греки ввели в позиционную систему современный знак 0 — нуль, произведя его, как полагает большинство специалистов, от первой буквы слова ????? — «ничто». При записи целых чисел (кроме числа 0) этот знак, естественно, не находил применения, ибо алфавитная система, которой пользовались греки, не была позиционной.

Современную систему записи чисел изобрели индийцы в начале VI в.н.э. Вавилонский позиционный принцип и греческий знак нуль для обозначения пустоты они применили не к основанию 60, а к основанию 10. Система получилась и последовательной, и экономной, и не противоречащей традиции, и чрезвычайно удобной для вычислений.

Индийцы передали свою систему арабам. В Европе позиционная система счисления появилась в XVI в. с переводом знаменитой арабской арифметики ал-Хорезми (ал-Хваризми). Она вступила в жестокую борьбу с традиционной римской системой и в конце концов одержала победу. Однако еще в XVI в. в Германии был издан и выдержал много изданий учебник арифметики, в котором используются исключительно «немецкие», т. е. римские цифры, или, лучше сказать, числа, так как в то время цифрами называли только знаки индийской системы. В предисловии автор пишет: «Я изложил эту счетную книгу обычными немецкими числами на благо и пользу непосвященному читателю (которому сразу трудно будет выучить цифры)». Десятичные дроби в Европе стали употреблять начиная с Симона Стевина (1548–1620).