Книга: Системное программное обеспечение. Лабораторный практикум

Описание используемого метода порождения результирующего кода

Для порождения результирующего кода будет использоваться рекурсивный алгоритм порождения списка триад на основе дерева синтаксического разбора. Схемы СУ-перевода для такого алгоритма были рассмотрены ранее (при выполнении лабораторной работы № 4).

В данном входном языке мы имеем следующие типы операций:

• логические операции (or, xor, and и not);

• операции сравнения (<, >, = и <>);

• арифметические операции (сложение, вычитание, унарное отрицание);

• оператор присваивания;

• полный условный оператор (if… then … else …) и неполный условный оператор (if… then…);

• оператор цикла с предусловием (while(…)do…);

• операции, не несущие смысловой нагрузки, а служащие только для создания синтаксических конструкций исходной программы (заголовок программы, операторные скобки begin…end, круглые скобки и точка с запятой).

Схемы СУ-перевода для арифметических операций (которые являются линейными операциями), оператора присваивания и условных операторов были построены при выполнении лабораторной работы № 4. Здесь их повторять не будем.

Схему СУ-перевода для оператора цикла с предусловием построим аналогично схемам СУ-перевода для условных операторов (которые были приведены на рис. 4.1 в лабораторной работе № 4).

Генерация кода для цикла с предусловием выполняется в следующем порядке:

• Порождается блок кода№ 1, вычисляющий логическое выражение, находящееся между лексемами while ((первая и вторая нижележащие вершины) и) (четвертая нижележащая вершина) – для этого должна быть рекурсивно вызвана функция порождения кода для третьей нижележащей вершины.

• Порождается команда условного перехода, которая передает управление в зависимости от результата вычисления логического выражения:

– в начало блока кода № 2, если логическое выражение имеет ненулевое значение;

– в конец оператора, если логическое выражение имеет нулевое значение.

• Порождается блок кода № 2, соответствующий операциям после лексемы do (пятая нижележащая вершина) – для этого должна быть рекурсивно вызвана функция порождения кода для шестой нижележащей вершины.

• Порождается команда безусловного перехода в начало блока кода № 1. Схема СУ-перевода для оператора цикла с предусловием представлена на рис. 5.2.

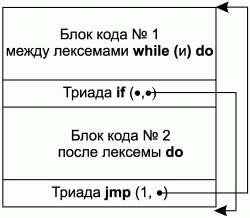
Рис. 5.2. Схема СУ-перевода для оператора цикла с предусловием.

Таким образом, для реализации оператора цикла достаточно иметь те же типы триад, которые необходимы для реализации условных операторов:

• IF(<операнд1>,<операнд2>) – триада условного перехода;

• JMP(1,<операнд2>) – триада безусловного перехода.

Смысл операндов для этих триад был описан при выполнении лабораторной работы № 4.

Отдельно следует остановиться на генерации кода для операций сравнения и логических операций. При выполнении лабораторной работы № 4 логические операции рассматривались как линейные операции и код для них строился соответствующим образом (аналогично коду для арифметических операций). Иной подход тогда не был возможен, поскольку тогда речь шла о побитовых логических операциях над целыми числами.

Однако в данном случае во входном языке логические операции выступают как операции булевой алгебры, которые выполняются только над двумя значениями: «истина» (1) и «ложь» (0). Исходными данными для них служат операции сравнения, результатом которых тоже могут быть только два указанных значения (константы типа «истина» (TRUE) и «ложь» (FALSE) во входном языке отсутствуют, но даже если бы они и были, суть дела это не меняет). При таких условиях возможно иное вычисление логических выражений, поскольку нет необходимости выполнять все операции:

• для операции OR нет необходимости вычислять выражение, если один из операндов TRUE, поскольку вне зависимости от другого операнда результат будет всегда TRUE;

• для операции OR нет необходимости вычислять выражение, если один из операндов FALSE, поскольку вне зависимости от другого операнда результат будет всегда FALSE.

Рассмотрим в качестве примера фрагмент кода для условного оператора:

if (a<b or a<c and b<c) a:=0 else a:=1;

При генерации кода для операций сравнения и логических операций как для линейных операций получим фрагмент последовательности триад:

1: < (a, b)

2: < (a, c)

3: < (b, c)

4: and (^2, ^3)

5: or (^1, ^4)

6: if (^5, ^9)

7::= (a, 0)

8: jmp (1, ^10)

9::= (a, 1)

Если же использовать свойства булевой алгебры, то можем получить следующий фрагмент последовательности триад:

1: < (a, b)

2: if01 (^3, ^7)

3: < (a, c)

4: if01 (^9, ^5)

5: < (b, c)

6: if01 (^9, ^7)

7::= (a, 0)

8: jmp (1, ^10)

9::= (a, 1)

Триада условного перехода IF01 здесь имеет следующий смысл: IF01(<операнд1>, <операнд2>) передает управление на триаду, указанную первым операндом, если предыдущая триада имеет значение 0 («Ложь»), иначе – передает управление на триаду, указанную вторым операндом.

Во втором варианте кода при том же количестве построенных триад в зависимости от значений переменных код будет в ряде случаев выполнять существенно меньше операций сравнения, чем в первом варианте, где при любых условиях выполняются все три операции. Правда, второй вариант кода содержит существенно больше операций передачи управления, что несколько снижает его эффективность на современных процессорах (передача управления нарушает конвейерную обработку данных, чего не происходит при линейной последовательности операций).

Разница в эффективности выполнения кода не столь велика, и ею можно было бы пренебречь, если бы операции сравнения не содержали вложенных операций. Например, при порождении кода для оператора по второму варианту:

if (a<b or F1(a)<c and b<c) a:=0 else a:=1;

функция F1 не будет вызвана, если выполняется условие a < b, а это уже принципиально важно.

Еще один пример:

if (a>0 and M[a]<>0) M[a]:=0;

также показывает преимущества второго варианта порождения кода. Если для этого фрагмента построить код по первому варианту, то вычисление выражения M[a] <> 0 может привести к выходу за границы массива M и даже к нарушению работы программы при отрицательных значениях переменной a, хотя в этом нет никакой необходимости – после того как не выполняется условие a>0, проверяющее левую границу массива M, нет надобности обращаться к условию M[a] <> 0. При порождении кода по второму варианту этого не произойдет, и данный оператор будет выполняться корректно.

Для того чтобы порождать код по второму варианту, схема СУ-перевода для логических операций и операций сравнения должна зависеть от вышележащих узлов синтаксического дерева – от вышележащих узлов ей в качестве параметров должны передаваться адреса передачи управления для значений «истина» и «ложь». Будем считать, что рассмотренные далее схемы СУ-перевода получают на вход два аргумента: адрес передачи управления для значения «истина» – А₁ и адрес передачи управления для значения «ложь» – А₂.

Схема СУ-перевода для операций сравнения будет выглядеть следующим образом:

1. Порождается блок кода для операции сравнения по схеме СУ-перевода для линейной операции.

2. Порождается триада IF01, первый аргумент которой – адрес А₂, а второй аргумент – адрес А₁.

Схема СУ-перевода для операции AND будет выглядеть следующим образом:

1. Порождается блок кода № 1 для первого операнда. Для этого рекурсивно вызывается функция порождения кода для первой нижележащей вершины, в качестве первого аргумента ей передается адрес блока кода № 2, а в качестве второго аргумента – адрес А₂.

2. Порождается блок кода № 2 для второго операнда. Для этого рекурсивно вызывается функция порождения кода для третьей нижележащей вершины, в качестве первого аргумента ей передается адрес А₁, а в качестве второго аргумента – адрес А₂.

Схема СУ-перевода для операции OR будет выглядеть следующим образом:

1. Порождается блок кода № 1 для первого операнда. Для этого рекурсивно вызывается функция порождения кода для первой нижележащей вершины, в качестве первого аргумента ей передается адрес А₁, а в качестве второго аргумента – адрес блока кода № 2.

2. Порождается блок кода № 2 для второго операнда. Для этого рекурсивно вызывается функция порождения кода для третьей нижележащей вершины, в качестве первого аргумента ей передается адрес А₁, а в качестве второго аргумента – адрес А₂.

Схема СУ-перевода для операции NOT будет выглядеть следующим образом:

Порождается блок кода для единственного операнда. Для этого рекурсивно вызывается функция порождения кода, в качестве первого аргумента ей передается адрес А₂, а в качестве второго аргумента – адрес А₁ (аргументы меняются местами).

Видно, что при использовании таких схем СУ-перевода логические операции фактически не порождают кода, а лишь определяют порядок вызова операций сравнения и ход передачи управления между ними. В приведенных описаниях схем есть одно логическое противоречие: необходимо передавать в качестве аргумента функции адрес блока кода, который еще не построен. Но при реализации этот момент можно обойти: например, передавать аргументом какое-то фиктивное значение (скажем, отрицательное число), а потом, после построения блока кода, менять его на известном интервале списка триад на вновь построенный адрес.[10]

Такой подход потребует изменить схемы СУ-перевода для условных операторов и для оператора цикла.

Для условных операторов генерация кода может выполняться в следующем порядке:

1. Порождается блок кода № 1, вычисляющий логическое выражение, находящееся между лексемами if (первая нижележащая вершина) и then (третья нижележащая вершина). Для этого должна быть рекурсивно вызвана функция порождения кода для второй нижележащей вершины, в качестве первого аргумента ей передается адрес блока кода № 2, а в качестве второго аргумента – адрес блока кода № 3 (для полного условного оператора) или адрес конца оператора (для неполного условного оператора).

2. Порождается блок кода № 2, соответствующий операциям после лексемы then (третья нижележащая вершина) – для этого должна быть рекурсивно вызвана функция порождения кода для четвертой нижележащей вершины (оба аргумента нулевые).

3. Для полного условного оператора порождается команда безусловного перехода в конец оператора.

4. Для полного условного оператора порождается блок кода № 3, соответствующий операциям после лексемы else (пятая нижележащая вершина) – для этого должна быть рекурсивно вызвана функция порождения кода для шестой нижележащей вершины (оба аргумента нулевые).

Генерация кода для цикла с предусловием выполняется в следующем порядке:

1. Порождается блок кода№ 1, вычисляющий логическое выражение, находящееся между лексемами while ((первая и вторая нижележащие вершины) и) (четвертая нижележащая вершина). Для этого должна быть рекурсивно вызвана функция порождения кода для третьей нижележащей вершины, в качестве первого аргумента ей передается адрес блока кода № 2, а в качестве второго аргумента – адрес конца оператора.

2. Порождается блок кода № 2, соответствующий операциям после лексемы do (пятая нижележащая вершина) – для этого должна быть рекурсивно вызвана функция порождения кода для шестой нижележащей вершины (оба аргумента нулевые).

3. Порождается команда безусловного перехода в начало блока кода № 1.

Современные компиляторы порождают различный код для логических операций:

• для побитовых операций порождается код как для линейных операций;

• для операций со значениями булевой алгебры по умолчанию порождается код по рассмотренной выше схеме (вычисление операции прерывается, как только ее значение становится известным).

Например, в языке Object Pascal код, порождаемый для операций and, or, xor и not, зависит от типов операндов (являются ли они логическими или целочисленными), а в языках C и C++ логические и побитовые операции даже обозначаются разными знаками операций. При этом в современных компиляторах существует команда, позволяющая разработчику отключить порождение «сокращенного» кода (обычно она называется «Complete Boolean evaluations») – тогда для всех логических выражений порождается полный линейный код.

В данной работе будут использованы схемы порождения линейного кода для операций сравнения и логических операций. Это допустимо, поскольку входной язык не допускает вложенных вызовов функций, обращений к массивам и других операций, которые могли бы приводить к побочным эффектам. Кроме того, и это наиболее важно, в работе должны быть проиллюстрированы методы оптимизации, работающие для линейных участков программы, поэтому желательно максимально увеличить количество линейных участков. При наличии конвейерной обработки команд в линейных процессорах на эффективности кода такой подход существенно не отразится.

Линейное порождение кода для логических операций существенно проще в реализации, и потому автор рекомендует именно его для выполняющих курсовую работу (результатом курсовой работы все-таки является простейший, а не промышленный компилятор).

Генерация кода для сокращенного вычисления логических выражений подробно рассмотрена в [2].

Оглавление книги