Книга: Основы объектно-ориентированного программирования
Простой класс
Что представляет собой класс можно выяснить, изучая простой, но типичный пример, который демонстрирует фундаментальные свойства, применимые практически ко всем классам.
Компоненты
Пример использует представление точки в двумерной графической системе:
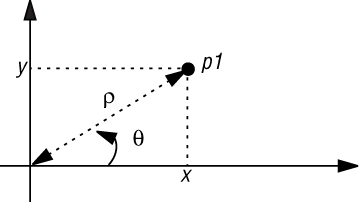
Рис. 7.1. Точка и ее координаты
Для определения типа POINT как абстрактного типа данных потребуется четыре функции-запроса: x, y, ?, ?. (В текстах подпрограмм для двух последних функций будут использоваться имена rho и theta). Функция x возвращает абсциссу точки (горизонтальную координату), y - ординату (вертикальную координату), ? - расстояние от начала координат, ? - полярный угол, отсчитываемый от горизонтальной оси. Значения x и y являются декартовыми, а ? и ? - полярными координатами точки. Другой полезной функцией является distance, возвращающая расстояние между двумя точками.
Далее спецификация АТД будет содержать такие команды, как translate (перемещение точки на заданное расстояние по горизонтали и вертикали), rotate (поворот на определенный угол вокруг начала координат) и scale (уменьшение или увеличение расстояния до начала координат в заданное число раз).
Нетрудно написать полную спецификацию АТД, включающую указанные функции и некоторые ассоциированные аксиомы. Далее в качестве примера приведены две из перечисленных функций:
x: POINT REAL
translate: POINT ? REAL ? REAL POINT
и одна из аксиом:
x (translate (p1, a, b)) = x (p1) + a
утверждающая, что для произвольной точки p1 и действительных значений a и b при трансляции точки на <a, b> абсцисса увеличивается на a.
Читатель, если пожелает, может самостоятельно завершить спецификацию АТД. В дальнейшей дискуссии подразумевается, что вы понимаете, как устроен данный АТД, вне зависимости от того, написали ли вы его полную формализацию или нет. Сосредоточим внимание на реализации АТД - классе.
Атрибуты и подпрограммы
Любой абстрактный тип данных и POINT в частности характеризуется набором функций, описывающих операции применимые к экземплярам АТД. В классе, реализующем АТД, функции становятся компонентами (features) - операциями, применимыми к экземплярам класса.
В лекции 6 было показано, что в АТД существуют функции трех видов: запросы (queries), команды (commands) и конструкторы (creators). Для компонентов классов необходима дополнительная классификация, основанная на том, каким образом реализован данный компонент - в пространстве или во времени (by space or by time). (См. "Категории функций", лекция 6)
Пример координат точки отчетливо демонстрирует эту разницу. Для точек доступны два общепринятых представления - в декартовых или полярных координатах. Если для представления выбрана декартова система координат, то каждый экземпляр класса содержит два поля представляющих координаты x и y соответствующей точки:
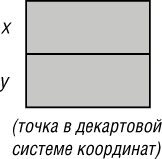
Рис. 7.2. Представление точки в декартовых координатах
Если p1 является такой точкой, то получение значений x и y сведется просто к просмотру соответствующих полей данной структуры. Однако определение значений ? и ? требует вычисления выражения ?(x2 + y2) для ? и arctg (y/x) для ? (при условии ненулевого x).
Использование полярной системы координат (рис. 7.3) приводит к противоположной ситуации. Теперь ? и ?доступны просто как значения полей, а определение x и y возможно после простых вычислений (? cos?, ? sin?, соответственно).
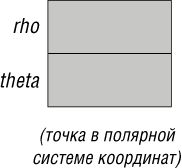
Рис. 7.3. Представление точки в полярных координатах
Приведенный пример указывает на необходимость рассмотрения компонентов двух видов:
[x]. Некоторые компоненты представлены в пространстве и, можно сказать, ассоциируются с некоторой частью информации каждого экземпляра класса. Они называются атрибутами (attributes). Для точки, представленной в декартовых координатах, атрибутами являются x и y, а в полярных координатах в роли атрибутов выступают rho и theta.
[x]. Другие компоненты представлены во времени, и для доступа к ним требуется описать некоторые вычисления (алгоритмы), применимые далее ко всем экземплярам данного класса. В дальнейшем они называются подпрограммами или методами класса (routines). В декартовом представлении точек - rho и theta это подпрограммы, а x и y выступают в качестве подпрограмм при использования полярных координат.
Вторая категория - подпрограммы - нуждается в дальнейшей дополнительной классификации. Часть подпрограмм возвращает результат, и их называют функциями (functions). В приведенном примере функциями являются x и y в представлении в полярных координатах, в то время как rho и theta - функции в декартовых координатах, все они возврвщают результат типа REAL. Подпрограммы, не возвращающие результат, соответствуют командам в спецификации АТД и называются процедурами (procedures). Например, класс POINT содержит процедуры translate, rotate и scale.
| Не следует путать понятие "функция", обозначающее в классах программу, возвращающую результат, с использованным ранее толкованием функции как математического описания операций АТД. Эта досадная путаница понятий обусловлена устоявшейся терминологией в математике и программировании. |
На рис. 7.4 дана рассмотренная выше классификация, представленная в виде дерева:
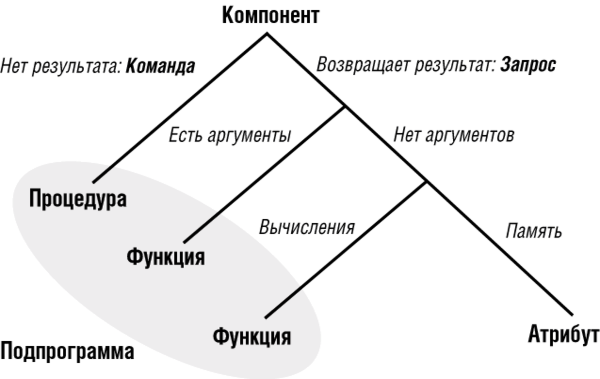
Рис. 7.4. Классификация компонентов класса по их роли
Эта классификация является внешней, основанной на том, каким образом данный компонент выглядит для использующего его клиента.
Можно предложить другую, внутреннюю классификацию, использующую в качестве основного критерия способ реализации компонента в классе:
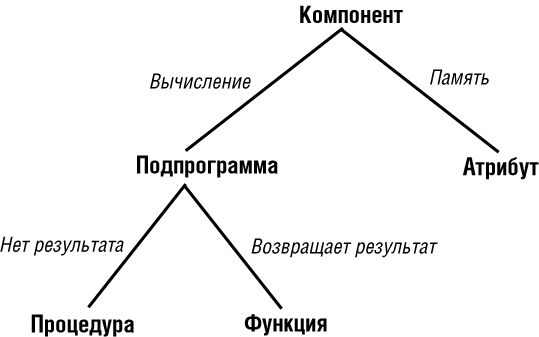
Рис. 7.5. Классификация компонентов класса по способу реализации
Унифицированный доступ
На первый взгляд один из аспектов приведенной выше классификации может вызывать беспокойство. Во многих случаях необходимо иметь возможность работать с объектом, например с точкой p1, не заботясь о том, какое внутреннее представление используется для p1 - декартово, полярное или иное. Необходимо ли для этого отличать атрибуты от функций?
Ответ зависит от того, с какой точки зрения рассматривать данную проблему - разработчика, автора данного класса POINT или клиента, создавшего класс, использующий POINT. Для разработчика разница между атрибутами и функциями принципиально важна и имеет смысл. Ему необходимо принимать решения о том, какие компоненты будут реализованы как данные в памяти и какие будут доступны в результате вычислений. Но заставлять клиента осознавать эту разницу, было бы серьезной ошибкой. Клиент должен обращаться к значениям x или ? для точки p1, не заботясь и не имея информации о том, как реализованы соответствующие запросы.
Решение проблемы дает принцип унифицированного доступа (Uniform Access principle), введенный в дискуссии о модульности (лекция 3). Принцип декларирует, что клиент должен иметь возможность доступа к свойствам объекта, используя одинаковую нотацию, вне зависимости от того, как это свойство реализовано - в памяти или как результат вычислений (в пространстве или во времени, в виде атрибута или подпрограммы). Этому важному принципу необходимо следовать при разработке нотации для обращения к компонентам класса. Так выражение, обозначающее значение компонента x объекта p1 будет всегда записываться в виде:
p1.x
вне зависимости от того, осуществляется ли доступ к полю данных объекта или выполняется подпрограмма.
| При использовании такой нотации неопределенность может возникать только для запросов без аргументов, которые могут быть реализованы и как функции и как атрибуты. Команда должна быть процедурой, запрос с аргументами должен быть функцией, так как атрибуты не могут иметь аргументов. |
Принцип унифицированного доступа необходим для гарантирования автономности компонентов ПО. Он защищает право создателя класса свободно экспериментировать с различными способами реализации, не создавая помех клиентам. (СМ. "Использование утверждений для документирования: краткая форма класса", лекция 11)
| Pascal, C и Ada нарушают этот принцип, предоставляя различную нотацию для вызова функций и для доступа к атрибутам. Это объяснимо для таких не ОО-языков (хотя еще в 1966 г. синтаксис Algol W предшественника Pascal удовлетворял этому принципу). Более новые языки, такие как C++ и Java, также не следуют этому принципу. Отход от этого принципа может служить причиной того, что изменения внесенные во внутренние представления (например переход от полярной системы координат к декартовой или иные) повлекут за собой неработоспособность многих клиентских классов. Это является одной из причин нестабильности программных разработок. |
Принцип унифицированного доступа является источником определенных требований и к подготовке документации. Последовательное применение этого принципа должно гарантировать, например, что в официальной документации не содержится сведений о том, является ли данный запрос без аргументов функцией или атрибутом. Это одно из требований к стандартной методике документирования классов, известной как краткая форма класса.
Класс POINT
Ниже приведена версия исходного текста класса POINT. Фрагменты, начинающиеся с двух тире "--", представляют собой комментарии, продолжающиеся до конца строки. Комментарии содержат пояснения, облегчающие понимание текста, и не влияют на семантику класса.
indexing
description: "Точка на плоскости"
class POINT feature
x, y: REAL
-- Абсцисса и ордината
rho: REAL is
-- Расстояние до начала координат (0, 0)
do
Result := sqrt (x^2 + y^2)
end
theta: REAL is
-- Полярный угол
do
-- Предлагается реализовать в качестве упражнения (упр. У7.3)
end
distance (p: POINT): REAL is
-- Расстояние до точки p
do
Result := sqrt ((x - p.x)^2 + (y- p.y)^2)
end
translate (a, b: REAL) is
-- Перемещение на a по горизонтали, b по вертикали
do
x := x + a
y := y + b
end
scale (factor: REAL) is
-- Изменение расстояния до начала координат в factor раз
do
x := factor * x
y := factor * y
end
rotate (p: POINT; angle: REAL) is
-- Поворот вокруг p на угол angle
do
-- Предлагается реализовать в качестве упражнения (упр. У7.3)
end
end
Некоторые аспекты приведенного текста неочевидны и требуют дополнительных разъяснений.
Класс в основном состоит из предложения, перечисляющего различные компоненты, вводимого ключевым словом feature. Кроме того, присутствует предложение indexing дающее общее описание (description), полезное для понимания функциональности класса, но никак не влияющее на семантику исполнения. Позднее будут рассмотрены три дополнительных предложения: inherit - для наследования; creation - при необходимости использования специального конструктора; invariant - для объявления инвариантов класса. Будет рассмотрена также возможность включения в класс двух или более предложений feature.
- СТРУКТУРА ПРОСТОЙ ПРОГРАММЫ
- ПРИМЕР ПРОСТОЙ ПРОГРАММЫ НА ЯЗЫКЕ СИ
- Еще один простой шаг к созданию сайта
- Простой клиент
- Практическая работа 38. Создание простой таблицы
- Практическая работа 44. Создание простой таблицы с формулами
- Создание простой панели управления email-маркетингом
- Простой сервер
- 10.8.1.2. Простой и легкий: sleep()
- Что такое простой текст?
- 19.5.1. Простой пример
- Комментарии к примеру простой системы "производитель




