Книга: Фундаментальные алгоритмы и структуры данных в Delphi

Компиляция регулярных выражений

Компиляция регулярных выражений

Следующий шаг состоит в создании NFA-автомата для регулярного выражения. Решение этой задачи мы начнем с создания блок-схемы конечного автомата выполнения регулярного выражения. Создание блок-схемы конечного автомата для конкретного регулярного выражения - достаточно простая задача. В общем случае правила языка утверждают, что регулярное выражение состоит из различных подвыражений (которые сами являются регулярными выражениями), скомпонованных или объединенных различными способами. Каждое подвыражение имеет единственное начальное состояние и единственное конечное состояние. И подобно тому, как это делается в конструкторе "Лего", эти простые строительные блоки собираются воедино, образуя все регулярное выражение. Блок-схема, приведенная на рис. 10.6, содержит конструкции, имеющие наибольшее значение.

Первый пример - конечный автомат, выполняющий распознавание отдельного символа алфавита. Второй пример столь же прост: он представляет собой конечный автомат, выполняющий распознавание любого символа алфавита (другими словами, это операция "."). Четвертая конструкция служит иллюстрацией того, как выполняется конкатенация (одного выражения, за которым следует второе). При этом мы просто объединяем начальное состояние второго подвыражения с конечным состоянием первого. Следующей показана конструкция, выполняющая дизъюнкцию. Мы создаем новое начальное состояние и получаем два возможных бесплатных перехода, по одному для каждого из подвыражений. Конечное состояние первого подвыражения объединяется с конечным состоянием второго подвыражения, и это последнее состояние становится конечным состоянием всего выражения. Следующий конечный автомат реализует операцию "?": в данном случае мы создаем новое начальное состояние с двумя ветвями е;

первая выполняет соединение с начальным состоянием подвыражения, а вторая - с его конечным состоянием. Это конечное состояние является конечным состоянием всего выражения. Вероятно, наиболее сложными конструкциями являются конечные автоматы для выполнения операций "+" и "*".

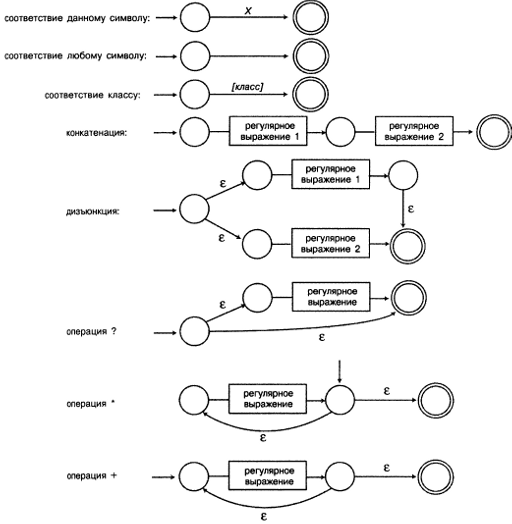
Рисунок 10.6. Конечные NFA-автоматы выполнения операций в регулярных выражениях

Если вы взглянете на рис. 10.6, то наверняка обратите внимание на ряд интересных свойств. В некоторых конструкциях для создания конечных автоматов определены и используются дополнительные состояния, но это делается вполне определенным образом: для каждого состояния существует один или два перехода из него, причем оба являются бесплатными. Это обусловлено веской причиной - в результате кодирование существенно упрощается.

Рассмотрим простой пример: регулярное выражение "(а|b)*bc" (повторенный ноль или более раз символ а или b, за которым следуют символы b и с). Используя описанные конструкции, можно шаг за шагом состроить конечный NFA-автомат для этого регулярного выражения. Последовательность действий показана на рис. 10.7. Обратите внимание, что на каждом шаге мы получаем конечный NFA-автомат с одним начальным и одним конечным состоянием, причем из каждого нового создаваемого состояния возможно не более двух переходов.

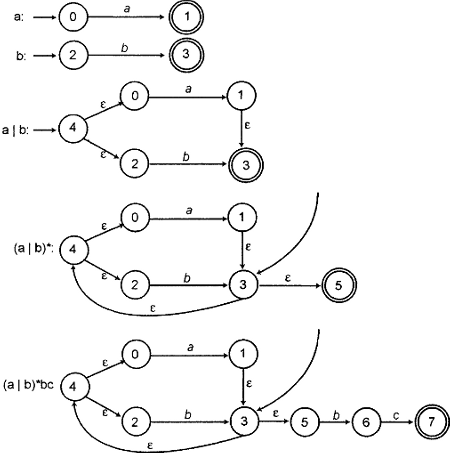
Рисунок 10.7. Пошаговое построение конечного NFA-автомата

Благодаря используемому методу конструирования, можно создать очень простое табличное представление каждого состояния. Каждое состояние будет представлено записью в массиве таких записей (номер состояния является индексом записи в массиве). Запись каждого состояния будет состоять из чего-либо для сравнения и двух номеров состояний для следующего состояния (NextStatel, NextState2). "Что-либо для сравнения" - это шаблон символов, с которым нужно устанавливать соответствие. Им может быть ветвь е, реальный символ, символ операции означающий соответствие с любым символом, класс символов (т.е. набор символов, один из которых должен совпадать с входным символом) или класс символов с отрицанием (входной символ не может быть частью набора, с которым устанавливается соответствие). Будучи построенным, этот массив известен под названием таблицы переходов (trAnsition table). В ней представлены все переходы из одного состояния в другое.

Используя заключительную блок-схему NFA-автомата, показанную на рис. 10.7, можно вручную построить таблицу переходов для регулярного выражения "(a|b)*bc". Результат приведен в таблице 10.1. Мы начинаем с состояния 0 и осуществляем переходы, выполняя сравнение с каждым символом во входной строке, пока не достигнем состояния 7. Реализация алгоритма установки соответствия, использующего подобную таблицу переходов, должна быть очень простой.

Таблица 10.1. Таблица переходов для выражения (a|b)*bc

Теперь, когда мы научились графически представлять NFA-автомат для конкретного регулярного выражения и узнали, что этот конечный NFA-автомат может быть представлен простой таблицей переходов, необходимо объединить оба алгоритма в анализаторе регулярных выражений, чтобы он мог выполнять непосредственную компиляцию таблицы состояний. После этого можно будет приступить к рассмотрению заключительной задачи - сопоставлению строк за счет использования таблицы переходов.

Прежде всего, необходимо выбрать способ представления таблицы состояний. Наиболее очевидный выбор - использование класса TtdRecordList, описанного в главе 2. Этот класс позволяет при необходимости увеличивать размер внутреннего массива. При этом заранее не нужно определять, сколько состояний может существовать для данного регулярного выражения.

В качестве подсказки будем использовать отдельные конструктивные блоки, показанные на рис. 10.6. Простейшим является выражение, которое распознает отдельный символ. Как видно из первой части рисунка 10.6, нам требуется начальное состояние, в котором будет выполняться распознавание символа, и которое будет иметь единственную связь с конечным состоянием (каждый из этих элементов будет также требоваться). Создадим простую подпрограмму, которая будет создавать новое состояние (как запись) и дописывать его в таблицу переходов. Код реализации этого простого метода приведен в листинге 10.7. Как видите, он принимает тип соответствия, символ, указатель на класс символов и две связи с другими состояниями. Конечно, не все из этих параметров будут требоваться для каждого создаваемого состояния. Но проще использовать один метод, который может создавать любой тип записи состояния, нежели целый набор таких методов, по одному для каждого возможного типа состояния.

Листинг 10.7. Добавление нового состояния в таблицу состояний

function TtdRegexEngine.rcAddState( aMatchType : TtdNFAMatchType;

aChar : AnsiChar; aCharClass : PtdCharSet;

aNextStatel: integer; aNextState2: integer): integer;

var

StateData : TNFAState;

begin

{определить поля в записи состояния}

if (aNextStatel = NewFinalState) then

StateData.sdNextState1 := succ(FTable.Count) else

StateData.sdNextState1 := aNextStatel;

StateData.sdNextState2 := aNextState2;

StateData.sdMatchType := aMatchType;

if (aMatchType = mtChar) then

StateData.sdChar := aChar else

if (aMatchType = mtClass) or (aMatchType = mtNegClass) then

StateData.sdClass := aCharClass;

{добавить новое состояние}

Result := FTable.Count;

FTable.Add(@StateData);

end;

При взгляде на первую часть рисунка 10.6 кажется, что для этой простой подпрограммы распознавания символа нужно создать два новых состояния. В действительности же можно ограничиться созданием только одного - начального состояния - и принять, что конечным состоянием будет следующее состояние, которое требуется добавить в список. Будем считать его "виртуальным" конечным состоянием. Если бы этот подход удалось применить в каждой из подпрограмм синтаксического анализа, можно было бы избавиться от необходимости создания конечного состояния, эквивалентного начальному состоянию другого подвыражения. Поэтому с этого момента будем считать, что все подпрограммы синтаксического анализа будут возвращать свое начальное состояние, и что конечное состояние, если оно действительно существует, будет номером индекса следующего состояния, которое необходимо добавить в таблицу переходов.

Из листинга 10.7 видно, что в действительности при передаче номера специального состояния NewFinalState в качестве номера следующего состояния мы определяем ссылку на индекс следующего элемента, который должен быть добавлен в таблицу переходов. Конечно, этот элемент еще не существует, но мы предполагаем, что он будет существовать, или что произойдет что-либо еще, позволяющее определить новую ссылку.

Код реализации метода распознавания отдельного символа приведен в листинге 10.8. Снова обратившись к листингу 10.5, обратите внимание на то, как был изменен первоначальный метод синтаксического анализа символа. Во-первых, мы больше не генерируем никаких исключений или сообщений об ошибках. Вместо этого мы возвращаем номер специального состояния ErrorState. Мы также отслеживаем код ошибки для каждой происходящей ошибки. Если какие-либо ошибки отсутствуют, новое состояние добавляется в таблицу переходов и возвращается как результат выполнения функции. Естественно, это состояние является начальным состоянием данного выражения. В действительности эта подпрограмма - метод класса машины обработки регулярных выражений.

Листинг 10.8. Синтаксический анализ отдельного символа и добавление его состояния

function TtdRegexEngine.rcParseChar : integer;

var

Ch : AnsiChar;

begin

{если встречается конец строки, это является ошибкой}

if (FPosn^ = #0) then begin

Result := ErrorState;

FErrorCode := recSuddenEnd;

Exit;

end;

{если текущий символ - один из метасимволов, это ошибка}

if FPosn^ in Metacharacters then begin

Result := ErrorState;

FErrorCode := recMetaChar;

Exit;

end;

{в противном случае состояние, соответствующее символу, добавляется в таблицу состояний}

{.. если он является отмененным символом: вместо него нужно извлечь следующий символ}

if (FPosn^ = '') then

inc(FPosn);

Ch := FPosn^;

Result := rcAddState(mtChar, Ch, nil, NewFinalState, UnusedState);

inc(FPosn);

end;

Это было достаточно просто, поэтому давайте рассмотрим другой, более сложный метод, который выполняет синтаксический анализ элемента. Первый случай - выражение заключенное в круглые скобки, - во многом подобен рассмотренному ранее: для него не нужно добавлять никакие новые состояния. Второй случай - класс символов или класс символов с отрицанием - определенно.нуждается в новом конечном автомате. Синтаксический анализ класса символов выполняется так же, как ранее (при этом он обрабатывается как набор диапазонов, каждый из которых может быть отдельным символом или двумя символами, разделенными дефисом). Однако на этот раз нужно записывать символы в класс. Для этого мы используем набор символов, распределенный в куче. Последним шагом является добавление в таблицу переходов нового состояния, которое распознает данный класс, подобно тому, как это было сделано для подпрограммы распознавания символов. Для заключительного случая, кроме уже рассмотренного конечного автомата для распознавания отдельного символа требуется конечный автомат для обработки символа операции "любой символ", т.е. точки ("."). Реализация этого конечного автомата достаточно проста: необходимо создать новое состояние, которое соответствует любому символу. Полный листинг подпрограммы синтаксического анализа элемента приведен в листинге 10.9. Как и в предыдущем случае, начальное состояние для этих выражений возвращается в качестве результата функции, а конечное состояние является виртуальным конечным состоянием.

Листинг 10.9. Синтаксический анализ <элемента> и вспомогательных компонентов

function TtdRegexEngine.rcParseAtom : integer;

var

MatchType : TtdNFAMatchType;

CharClass : PtdCharSet;

begin

case FPosn^ of

'(' : begin

{обработка открывающей круглой скобки}

inc(FPosn);

{синтаксический анализ всего регулярного выражения, заключенного в круглые скобки}

Result := rcParseExpr;

if (Result = ErrorState) then

Exit;

{если текущий символ не является закрывающей круглой скобкой, имеет место ошибка}

if (FPosn^ <> ')') then begin

FErrorCode := recNoCloseParen;

Result := ErrorState;

Exit;

end;

{обработка закрывающей круглой скобки}

inc(FPosn);

end;

'[':

begin

{обработка открывающей квадратной скобки}

inc(FPosn);

{если первый символ класса - ' ^' то класс является классом с отрицанием, в противном случае это обычный класс}

if (FPosn^ = '^') then begin

inc(FPosn);

MatchType := mtNegClass;

end

else begin

MatchType :=mtClass;

end;

{выделить набор символов класса и выполнить синтаксический анализ класса символов; в результате возврат будет выполнен либо в случае сшибки, либо при обнаружении закрывающей квадратной скобки}

New(CharClass);

CharClass^ := [];

if not rcParseCharClass (CharClass) then begin

Dispose(CharClass);

Result := ErrorState;

Exit;

end;

{обработка закрывающей квадратной скобки}

inc(FPosn);

{добавить новое состояние для класса символов}

Result := rcAddState(MatchType, #0, CharClass, NewFinalState, UnusedState);

end;

'.':

begin

{обработка метасимвола точки}

inc(FPosn);

{добавить новое состояние для лексемы 'любой символ'}

Result := rcAddState(mtAnyChar, #0, nil,

NewFinalState, UnusedState);

end;

else

{в противном случае - выполнить синтаксический анализ отдельного символа}

Result := rcParseChar;

end; {case}

end;

До сих пор мы создавали состояния без каких-либо ссылок состояний друг на друга. Но если вы обратитесь к блок-схеме конечного NFA-автомата для операции п|", то увидите, что, в конце концов, некоторые состояния приходится объединять друг с другом. Необходимо сохранить начальные состояния для каждого подвыражения и нужно создать новое начальное состояние, которое будет связано бесплатными связями с каждым из этих двух состояний. Заключительное состояние первого подвыражения должно быть связано с заключительным состоянием второго подвыражения, которое после этого становится конечным состоянием выражения дизъюнкции.

Однако это сопряжено с небольшой проблемой. Заключительное состояние для первого выражения не существует. Поэтому его нужно создать, но это следует сделать осторожно, чтобы остальные состояния не стали ошибочно указывать на него.

Естественно, прежде всего, необходимо выполнить синтаксический анализ исходного <члена>. Мы получим начальное состояние (поэтому сохраним его в переменной). При этом известно, что конечное состояние является виртуальным конечным состоянием, следующим непосредственно за концом списка. Если следующим символом является " |", это свидетельствует о выполнении синтаксического анализа дизъюнктивной конструкции и о необходимости синтаксического анализа следующего <выражения>. Именно здесь нужно проявить повышенную осторожность. Перво-наперво, мы создаем состояние для конечного состояния этого исходного <члена>. В данный момент, нас не волнует, на какие состояния указывают его связи. Вскоре они будут исправлены. Создание этого конечного состояния означает также, что любые состояния в <члене>, указывающие на виртуальное конечное состояние, фактически будут указывать на состояние, которое мы только что сделали реальным. Теперь нужно создать начальное состояние дизъюнкции. Нам известна одна из связей (исходный <член> ), но еще не известна вторая. В конце концов, синтаксический анализ второго < выражения> еще не был выполнен. Теперь мы можем его выполнить. Мы получим начальное состояние, которое используем для исправления второй связи в начальном состоянии дизъюнкции. Новое виртуальное конечное состояние может быть использовано для создания связи, исходящей из конечного состояния исходного <члена>.

В результате выполнения всех этих манипуляций нам пришлось создать два новых состояния (первое является начальным состоянием для дизъюнкции, а второе -конечным состоянием исходного <члена> ). При этом мы проявили достаточную осмотрительность, чтобы виртуальное конечное состояние второго < выражения> было виртуальным конечным состоянием всей операции дизъюнкции. Код реализации этого конечного автомата приведен в листинге 10.10 (обратите внимание, что был создан еще один метод, который определяет связи для состояния после его создания).

Листинг 10.10. Синтаксический анализ операции "|"

function TtdRegexEngine.rcSetState(aState : integer;

aNextStatel: integer;

aNextState2: integer): integer;

var

StateData : PNFAState;

begin

{извлечь запись состояния и изменить информацию о переходе}

StateData := PNFAState(FTable[aState])/ StateData^.sdNextState1 := aNextStatel/ StateData^.sdNextState2 := aNextState2;

Result := aState;

end;

fmiction TtdRegexEngine.rcParseExpr : integer;

var

StartStatel : integer;

StartState2 : integer;

EndState1 : integer;

OverallStartState : integer;

begin

{предположим, что имеет место наихудший случай}

Result ErrorState;

{выполнить синтаксический анализ исходного члена}

StartStatel := rcParseTerm;

if (StartStatel = ErrorState) then

Exit;

{если текущий символ является *не* символом вертикальной черты, дизъюнкция отсутствует, поэтому начальное состояние исходного члена необходимо вернуть в качестве текущего начального состояния}

if (FPosn^ <> '|') then

Result := StartStatel {в противном случае необходимо выполнить синтаксический анализ второго выражения и объединить их в таблице переходов}

else begin

{обработать символ вертикальной черты}

inc(FPosn);

{конечное состояние исходного члена еще не существует (хотя член и содержит состояние, которое указывает на него), поэтому его нужно создать}

EndState1 := rcAddState(mtNone, #0, nil, UnusedState, UnusedState);

{для конструкции ИЛИ требуется новое начальное состояние: оно будет указывать на исходный член и на второе выражение, синтаксический анализ которого будет выполняться следующим}

OverallStartState := rcAddState(mtNone, #0, nil,

UnusedState, UnusedState);

{выполнить синтаксический анализ следующего выражения}

StartState2 := rcParseExpr;

if (StartState2 = ErrorState) then

Exit;

{изменить состояние, определенное для всего выражения, чтобы вторая связь указывала на начало второго выражения}

Result := rcSetState(OverallStartState, StartStatel, StartState2);

{определить конечное состояние исходного члена, чтобы оно указывало на результирующее конечное состояние, определенное для второго выражения и всего выражения в целом}

rcSetState(EndState1, FTable.Count, UnusedState);

end;

end;

После ознакомления с этой конкретной конструкцией создание конечных автоматов для операций замыкания ("*", и+" и сложности не представляет. Важно только создавать состояния в правильном порядке. Рассмотрим код, приведенный в листинге 10.11.

Листинг 10.11. Синтаксический анализ операций замыкания

function TtdRegexEngine.rcParseFactor : integer;

var

StartStateAtom : integer;

EndStateAtom : integer;

begin

{предположим худшее}

Result := ErrorState;

{вначале выполнить синтаксический анализ элемента}

StartStateAtom := rcParseAtom;

if (StartStateAtom = ErrorState) then

Exit;

{проверить на наличие операции замыкания}

case FPosn^ of

' ?' : begin

{обработать символ операции ?}

inc(FPosn);

{конечное состояние элемента еще не существует, поэтому его нужно создать}

EndStateAtom := rcAddState(mtNone, #0, nil,

UnusedState, UnusedState);

{создать новое начальное состояние для всего регулярного выражения}

Result := rcAddState(mtNone, #0, nil,

StartStateAtom, EndStateAtom);

{обеспечить, чтобы новое конечное состояние указывало на следующее еще не использованное состояние}

rcSetState(EndStateAtom, FTable.Count, UnusedState);

end;

' *' : begin

{обработать символ операции *}

inc(FPosn);

{конечное состояние элемента еще не существует, поэтому его нужно создать; оно будет начальным состоянием всего подвыражения регулярного выражения}

Result := rcAddState(mtNone, #0, nil,

NewFinalState, StartStateAtom);

end;

' + ' : begin

{обработать символ операции +}

inc(FPosn);

{конечное состояние элемента еще не существует, поэтому его нужно создать}

rcAddState(mtNone, #0, nil, NewFinalState, StartStateAtom);

{начальное состояние всего подвыражения регулярного выражения будет начальным состоянием элемента}

Result := StartStateAtom;

end;

else

Result := StartStateAtom;

end; {case}

end;

При выполнении ноля или одного замыкания (операции "?") нужно создать конечное состояние элементарного выражения, к которому применяется операция, и начальное состояние всего конечного автомата. Эти новые состояния связаны между собой, как показано на рис. 10.5.

При выполнении ноля или более замыканий (операции "*") задача еще проще: нужно создать только конечное состояние для элемента. Оно становится начальным состоянием всего выражения. При этом виртуальное конечное состояние является конечным состоянием выражения.

При выполнении одного или более замыканий (операции "+") задача почти столь же проста. Потребуется создать конечное состояние для элемента и связать его с начальным состоянием элемента (которое является также начальным состоянием выражения). При этом виртуальное конечное состояние снова является конечным состоянием выражения.

Теперь осталось написать код только для выполнения операции конкатенации. На рисунке 10.6 эта операция выглядит просто: конечное состояние первого подвыражения становится начальным состоянием второго, и эти подвыражения связаны одно с другим. На практике не все так просто. Конечное состояние первого выражения является виртуальным конечным состоянием, причем не существует никакой гарантии, что оно будет совпадать с начальным состоянием следующего выражения (в этом случае они были бы автоматически связаны). Нет, вместо этого необходимо создать конечное состояние первого выражения и связать его с начальным состоянием второго выражения. Код решения этой последней задачи, включая создание заключительного конечного состояния, приведен в листинге 10.12.

На данный момент мы успешно связали аспекты синтаксического анализа и компиляции, что позволяет принять регулярное выражение и выполнить его синтаксический анализ с целью генерации скомпилированной таблицы переходов. На этапе компиляции программа определит и сохранит начальное состояние полного конечного NFA-автомата для регулярного выражения.

Однако прежде чем приступать к компиляции, необходимо выполнить несколько дополнительных действий для некоторого повышения эффективности. В ряде случаев нам приходилось добавлять некоторые состояния, выход из которых был связан всего с одним бесплатным переходом, причем самым неприятным был случай, когда дополнительное состояние требовалось для выполнения конкатенации.

Листинг 10.12. Синтаксический анализ конкатенации

function TtdRegexEngine.rcParseTerm : integer;

var

StartState2 : integer;

EndState1 : integer;

begin

{выполнить синтаксический анализ исходного коэффициента; возращенный при этом номер состояния буде также номером возвращаемого состояния}

Result := rcParseFactor;

if (Result = ErrorState) then

Exit;

if (FPosn^ = '(') or (FPosn^ = '[') or (FPosn^ = '.') or

((FPosn^ <> #0) and not (FPosn^ in Metacharacters)) then begin

{конечное состояние исходного коэффициента еще не существует (хотя член и содержит состояние, которое указывает на него), поэтому его нужно создать}

EndState1 := rcAddState(mtNone, #0, nil, UnusedState, UnusedState);

{выполнить синтаксический анализ следующего члена}

StartState2 := rcParseTerm;

if (StartState2 = ErrorState) then begin

Result := ErrorState;

Exit;

end;

{объединить первый коэффициент со вторым членом}

rcSetState(EndState1, StartState2, UnusedState);

end;

end;

Естественно, состояния с единственным переходом для выхода приводят к нерациональной трате времени. Поэтому необходимо выполнить оптимизацию, исключив их из таблицы переходов. Такие состояния называются фиктивными.

Однако вместо того, чтобы их удалять, мы просто их пропустим. Соответствующий алгоритм достаточно прост: необходимо выполнить считывание всех состояний. Для каждого состояния необходимо следовать по ссылке, указанной в его поле NextStatel. Если она устанавливает связь с одним из фиктивных состояний, связь нужно заменить связью NextStatel фиктивного состояния. Это же потребуется выполнить для связи NextState2 каждого состояния, если она существует. Код выполнения этой итерационной процедуры приведен в листинге 10.13.

Листинг 10.13. Оптимизация фиктивных состояний

procedure TtdRegexEngine.rcLevel1Optimize;

var

i : integer;

Walker : PNFAState;

begin

{оптимизация первого уровня удаляет все состояния, которые содержат только один бесплатный переход к другому состоянию}

{циклически обработать все записи состояний, кроме последней}

for i := 0 to (FTable.Count - 2) do

begin {получить данное состояние}

with PNFAState (FTable [ i ])^ do

begin

{выполнить проход по цепочке, указанной первым следующим состоянием, и разорвать связи с состояниями, которые являются простыми одиночными бесплатными переходами}

Walker := PNFAState(FTable[sdNextState1]);

while (Walker^.sdMatchType = mtNone) and

(Walker^.sdNextState2 = UnusedState) do

begin

sdNextState1 := Walker^.sdNextState1;

Walker := PNFAState(FTable[sdNextState1]);

end;

{выполнить проход по цепочке, указанной вторым следующим состоянием, и разорвать связи с состояниями, которые являются простыми одиночными бесплатными переходами}

if (sdNextState2 <> UnusedState) then begin

Walker := PNFAState(FTable[sdNextState2]);

while (Walker^.sdMatchType = mtNone) and

(Walker^.sdNextState2 = UnusedState) do

begin

sdNextState2 := Walker^.sdNextState1;

Walker := PNFAState(FTable[sdNextState2]);

end;

end;

end;

end;

end;

Оглавление книги