Книга: Аналитическая культура

Проблемы типа «ближайший сосед»

Проблемы типа «ближайший сосед»

Первый тип проблем можно условно назвать «ближайший сосед». Халеви и др. приводят пример:

Рисунок 1 Хейса и Эфроса

Норвиг изобразил следующую зависимость:

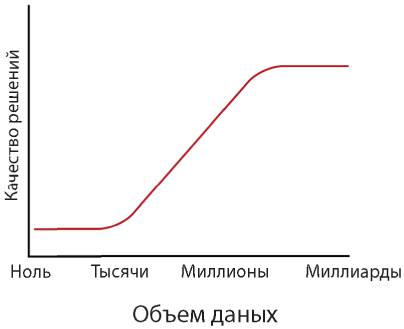
и описал ее как «порог данных», при котором результаты из очень плохих стали очень хорошими.

Я не уверен, что существует какая-то пороговая величина или что-то напоминающее фазовый переход. Скорее, мне кажется, суть проблемы заключается в поиске ближайшего соответствия. Чем больше данных, тем ближе может быть соответствие.

Хейс и Эфрос отмечают:

Размеры двух этих наборов данных различаются слишком сильно, а «качественный скачок» — это не то же самое, что порог (буквально фазовый переход).

Увеличение объема данных может значительно повлиять на показатели из-за простых эффектов. Например, рассмотрим выборку размера n в стандартном нормальном распределении. Как изменяется в зависимости от значения n минимальное значение этой выборки? Создадим выборки разных размеров и вычислим минимальное значение с помощью следующего кода R:

x<-seq(1,7,0.5)

y<-vector(mode="numeric",length=length(x))

for (i in 1:length(x)){ y[i] <- min(rnorm(10^(x[i]))) }

plot(x,y,xlab="Sample size, n (log10 scale)",

ylab="Minimum value of sample",type="b")

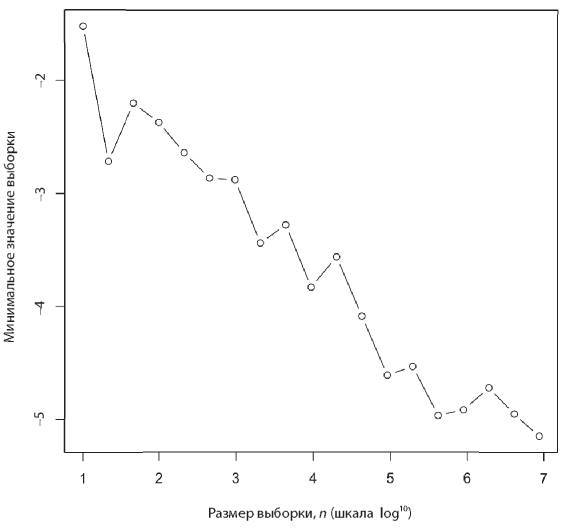
Минимум уменьшается лог-линейно. Это случай экстремума с позиции неограниченного хвоста. Возможно, более подходящей здесь для проблемы минимизации, такой как подбор соответствия, будет нижняя граница — идеальное соответствие для всех целей. Например, возможно, кто-то еще, стоя на том же самом месте, сделал фотографию того же самого вида, но без предмета, портящего фотографию.

Думаю, именно это происходит на графике Норвига. При определенном размере выборки мы нашли очень хорошее соответствие, и увеличение размера выборки уже не может улучшить результат.

Подведем итог: для проблемы минимизации типа «ближайший сосед» с неотрицательной функцией расстояния (что означает, что нижняя граница функции ошибки обучения (cost function) равна нулю) функция расстояния в среднем будет монотонно убывать с размером выборки или данных.

Оглавление книги