Книга: Этюды для программистов
Как раскрыть шифр
Как раскрыть шифр
Будем предполагать, что криптограмма мисс Хари получена при помощи квадрата Виженера, хотя бы по той причине, что он — ее соотечественник. Если наше предположение неверно, методы решения позволят обнаружить это. Если бы сообщение было зашифровано при помощи простой подстановки, то расшифровать его можно было бы, подсчитав количество появлений каждой буквы в шифрованном тексте, поделив это количество на длину сообщения и сравнив полученные величины с частотами букв русского алфавита, приведенными на рис. 24.5. Для сообщений такой длины, как наше, распределения частот, если выписать их в убывающем порядке, почти полностью совпадут, и, таким образом, для каждой буквы исходного текста откроется ее двойник в шифрованном тексте. Но для квадрата Виженера такой простой метод уже не сработает. Необходимо определить не только смешанный алфавит, но и ключевое слово; поскольку каждый из этих элементов искажен другим, то трудно даже догадаться, с какого конца начать.
О .0940
А .0896
Е .0856
И .0739
Н .0662
Т .0611
Р .0561
С .0554
П .0421
М .0417
В .0400
Л .0358
К .0322
Л .0280
Я .0243
Ы .0225
Б .0197
3 .0193
У .0179
Г .0153
Ь .0125
Ч .0118
Й .0094
X .0093
Ц .0087
Ж .0064
Ю .0063
Щ .0048
Ф .0034
Э .0033
Ш .0032
Ъ .0002
Рисунок 24.5. Таблица частот букв русского алфавита. Получена по текстам нескольких препринтов, издававшихся в ИПМ АН СССР им. М. В. Келдыша.
Правильной отправной точкой будет нахождение длины ключевого слова. Обратите внимание, что в примере на рис. 24.4 первая, пятая, девятая, … буквы исходного текста зашифрованы при помощи одного и того же смешанного алфавита Л. Если рассматривать лишь каждую четвертую букву шифрованного текста, то получим распределение частот, подобное распределению для букв русского алфавита, поскольку буквы в этих позициях зашифрованы при помощи одного и того же смешанного алфавита, т. е. при помощи простой подстановки. Аналогично если взять каждую четвертую букву шифрованного текста, начиная со второй, третьей или четвертой позиции, то снова получим распределение частот как для букв русского алфавита. Существует способ измерить, насколько данное распределение частот подобно распределению букв алфавита. Рассмотрим индекс совпадения
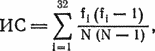
где fi — количество появлений i-й буквы, а N — общее число рассматриваемых букв. Если все буквы рассматриваемого подмножества текста зашифрованы при помощи одного алфавита, то этот индекс совпадения должен иметь значение больше 0.045 и, вероятно, меньше 0.065 (теоретическое значение равно 0.055). Исходя из этого, алгоритм определения длины ключевого слова будет таким.
Шаг 1. Для i от 1 до 20 предположить, что длина ключевого слова равна i, и выполнить шаги 2, 3, 4. Мы выбрали верхнюю границу равной 20 лишь для удобства. Разумеется, ключевое слово может быть и длиннее.
Шаг 2. Для j от 1 до i выполнить шаг 3. В этих двух шагах будут вычислены i различных значений НС.
Шаг 3. Построить распределение числа появления букв в позициях j, i + j, 2i + j, …, т. е. в каждой i-й цозиции, начиная с j-й позиции. По формуле, приведенной выше, вычислить ИСj для полученного распределения. В качестве N в этой формуле нужно использовать число букв в данном подмножестве текста, а не длину всего текста.
Шаг 4. Если все значения ИС1, ИС2, …, ИСi больше 0.045, то, вероятно, i кратно длине ключевого слова. Если только один из ИС меньше 0.045, то i также может быть кратно длине ключевого слова.
Проверить длину ключевого слова можно и другим способом. Найдите два места в шифрованном тексте, где две одинаковые буквы идут в том же порядке, например ЦМ в позициях 19 и 54 на рис. 24.1. Такое повторение могло произойти по двум разным причинам. Возможно, в соответствующих местах исходного текста были различные сочетания букв, которым отвечали разные части ключевого слова, и они случайно отобразились в одинаковые сочетания букв, либо в исходном тексте были повторения, которые попали на одинаковые части ключевого слова, и, таким образом, оказались зашифрованными дважды одним и тем же способом. Во втором случае расстояние между началами повторяющихся сочетаний букв должно быть кратно длине ключевого слова. К сожалению, невозможно определить, по какой из двух причин произошло повторение данного сочетания букв: случайное повторение пар букв в шифрованном тексте довольно частое явление. Но если в шифрованном тексте повторяются сочетания из трех или более букв, то вероятность того, что это повторение произошло случайно, а не в результате повторения ключа, очень мала (для сочетаний из четырех и более букв она практически нулевая). Таким образом, другой способ выявления длины ключевого слова — отыскать в шифрованном тексте все пары повторяющихся групп из трех и более букв и измерить расстояния между ними. Число, которое делит 90% или более из этих расстояний, — прекрасный претендент на роль длины ключевого слова. Данная проверка вместе с вычислением значений ИС однозначно определяет длину ключевого слова.
Предположим, нам удалось выяснить, что длина ключевого слова равна k. Тогда первоначальный шифрованный текст можно разбить на k групп G1, G2, …, Gk, где каждая группа начинается с позиции i, 1 ? i ? k, и содержит каждую k-ю букву текста, начиная с i-й буквы. Каждая из этих к групп была зашифрована при помощи только одного алфавита, т. е. при помощи простой подстановки. Остается в каждой группе для каждой шифрованной буквы определить ее эквивалент в исходном тексте. Но здесь у нас имеется хорошее подспорье. Если бы был известен алфавит, по которому была зашифрована какая-нибудь из групп, то алфавит, по которому была зашифрована любая другая группа, можно было бы найти путем циклического сдвига уже известного алфавита на некоторое число букв. С другой стороны, определить исходные эквиваленты букв было бы проще, если бы удалось распределения числа появлений букв для различных групп скомбинировать в одно обобщенное распределение, поскольку, чем больше данных было использовано для построения какого-либо распределения, тем достовернее будут сделанные на его основе статистические выводы. Для построения такой комбинации необходимо знать относительные сдвиги между алфавитами, использованными для шифрования различных групп.
Относительные сдвиги находятся при помощи некой модификации индекса совпадения. Построим для каждой группы Gi распределение числа появлений букв и запишем его в алфавитном порядке шифрованных букв. В табл. 24.1 показаны распределения для сообщения, приведенного на рис. 24.1, в предположении, что k = 7. Пусть fi, ? — количество появлений буквы ? алфавита i; определим функцию
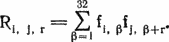
Считается, что если ? + r больше 32, то происходит циклический возврат к началу алфавита. Чем больше значение Ri, j, r, тем больше вероятность того, что алфавит для группы j в квадрате Виженера находится на r позиций ниже алфавита для группы i. Вычислим все значения Ri, j, r (для j ? i их можно не вычислять благодаря свойству симметрии) и выберем i и j, которые дают максимальное значение Ri, j, r. Вероятно, группа j сдвинута на r позиций относительно группы i.
Из групп Gi и Gj построим новую супергруппу Gij, положив величину fij, ? равной fi, ? + fi, ?+r. Отбросим из рассмотрения группы Gi и Gj, заменив их группой Gij, и повторим описанный в последних двух абзацах процесс. После k ? 1 повторений станут известны относительные сдвиги для всех k алфавитов. Кроме того, будет найдено обобщенное распределение частот. Для того чтобы найти исходные эквиваленты букв шифрованного текста, переупорядочим последние согласно их частотам. В результате буквы шифрованного текста должны расположиться в том же порядке, что и буквы русского алфавита (см. рис. 24.5). Теперь нетрудно восстановить весь квадрат Виженера и расшифровать текст. Ключевое слово можно найти, перебрав 32 набора из к букв, относительные расстояния между которыми соответствуют найденным сдвигам алфавитов. Возможно, что некоторые редко встречающиеся буквы окажутся не на своих местах. Эту ситуацию можно поправить при помощи визуального исследования полученного текста. Следует восстановить и смешанный алфавит, и ключевое слово, поскольку они оба могут иметь некоторую психологическую связь с содержанием сообщения и их выявление поможет дополнительно убедиться в правильности решения. Между прочим, что же написала мисс Хари?
| Таблица 24.1. Распределения для сообщения с рис. 24.1 при k = 7 | |||||||||||||
| G1 | G2 | G3 | G4 | G5 | G6 | G7 | |||||||
| A | 5 | A | 0 | A | 3 | A | 2 | A | 8 | A | 0 | A | 3 |
| Б | 1 | Б | 7 | Б | 0 | Б | 1 | Б | 0 | Б | 1 | Б | 3 |
| В | 19 | В | 5 | В | 6 | В | 4 | В | 1 | В | 1 | В | 8 |
| Г | 0 | Г | 13 | Г | 2 | Г | 10 | Г | 5 | Г | 2 | Г | 8 |
| Д | 1 | Д | 0 | Д | 0 | Д | 4 | Д | 0 | Д | 0 | Д | 5 |
| Е | 4 | Е | 3 | Е | 1 | Е | 0 | Е | 2 | Е | 2 | Е | 11 |
| Ж | 10 | Ж | 8 | Ж | 3 | Ж | 7 | Ж | 3 | Ж | 2 | Ж | 1 |
| 3 | 3 | 3 | 7 | 3 | 9 | 3 | 2 | 3 | 2 | 3 | 5 | 3 | 4 |
| И | 2 | И | 3 | И | 4 | И | 4 | И | 2 | И | 0 | И | 3 |
| Й | 4 | Й | 0 | Й | 0 | Й | 1 | Й | 6 | Й | 1 | Й | 0 |
| К | 2 | К | 9 | К | 4 | К | 9 | К | 1 | К | 4 | К | 3 |
| Л | 3 | Л | 6 | Л | 4 | Л | 2 | Л | 1 | Л | 7 | Л | 3 |
| М | 5 | М | 1 | М | 0 | М | 5 | М | 4 | М | 14 | М | 0 |
| Н | 1 | Н | 6 | Н | 9 | Н | 3 | Н | 2 | Н | 3 | Н | 1 |
| О | 0 | О | 4 | О | 2 | О | 8 | О | 1 | О | 1 | О | 4 |
| Л | 1 | Л | 0 | Л | 1 | Л | 4 | Л | 9 | Л | 4 | Л | 0 |
| Р | 1 | Р | 2 | Р | 12 | Р | 2 | Р | 2 | Р | 0 | Р | 5 |
| С | 5 | С | 0 | С | 0 | С | 0 | С | 2 | С | 6 | С | 1 |
| Т | 1 | Т | 0 | Т | 5 | Т | 0 | Т | 3 | Т | 1 | Т | 1 |
| У | 2 | У | 7 | У | 6 | У | 1 | У | 9 | У | 4 | У | 2 |
| Ф | 0 | Ф | 1 | Ф | 9 | Ф | 4 | Ф | 5 | Ф | 5 | Ф | 5 |
| X | 4 | X | 0 | X | 0 | X | 0 | X | 4 | X | 3 | X | 2 |
| Ц | 3 | Ц | 0 | Ц | 1 | Ц | 3 | Ц | 8 | Ц | 1 | Ц | 3 |
| Ч | 10 | Ч | 0 | Ч | 0 | Ч | 2 | Ч | 8 | Ч | 0 | Ч | 1 |
| Ш | 5 | Ш | 8 | Ш | 2 | Ш | 4 | Ш | 2 | Ш | 1 | Ш | 2 |
| Щ | 0 | Щ | 0 | Щ | 4 | Щ | 0 | Щ | 0 | Щ | 1 | Щ | 8 |
| Ъ | 0 | Ъ | 6 | Ъ | 4 | Ъ | 4 | Ъ | 0 | Ъ | 9 | Ъ | 5 |
| Ы | 3 | Ы | 0 | Ы | 1 | Ы | 8 | Ы | 2 | Ы | 8 | Ы | 0 |
| Ь | 1 | Ь | 5 | Ь | 9 | Ь | 5 | Ь | 4 | Ь | 2 | Ь | 0 |
| Э | 8 | Э | 0 | Э | 0 | Э | 0 | Э | 4 | Э | 0 | Э | 6 |
| Ю | 1 | Ю | 0 | Ю | 1 | Ю | 3 | Ю | 4 | Ю | 5 | Ю | 4 |
| Я | 1 | Я | 5 | Я | 4 | Я | 3 | Я | 1 | Я | 12 | Я | 3 |
Значение R1, 0, 2 равно 333, а значение R3, 6, 12 равно 335. Значение R3, 6, 12 получается перемножением чисел появлений букв от А до У для G3 на числа появлений букв от М до Я для G6 и чисел появлений букв от Ф до Я для G3 на числа появлений букв от А до Л для G6 и сложением всех этих произведений.
Тема. Напишите программу, которая в качестве входных данных воспринимает шифрованное сообщение и, в предположении, что оно зашифровано по схеме Виженера, печатает расшифрованный текст. Программа должна также печатать квадрат Виженера и ключевое слово, которые она вычисляет в процессе решения задачи. Специальные входные параметры должны управлять выводом промежуточных результатов, таких, как, например, все возможные длины ключевого слова, распределения частот букв для отдельных алфавитов, значения ИС и т. д., которые нужны для контроля. Эти результаты могут быть полезны при отладке, а также в тех, к сожалению, вполне реальных ситуациях, когда предложенное машиной решение оказалось не совсем точным. Четкость оформления выводных данных имеет большое значение: бестолковые распечатки лишь затрудняют работу интуиции специалиста по расшифровке сообщений.
Указания исполнителю. Описанные здесь алгоритмы вполне понятны и легко реализуются, но обладают одним неприятным свойством — они не дают однозначного результата. Длина ключевого слова, например, будет лишь «вероятной», так что необходимо еще сделать обоснованный выбор одной из возможных длин. Аналогично алгоритмическое определение исходных эквивалентов для редко встречающихся букв шифрованного текста следует проверить, убедившись, что при расшифровке получаются правильные русские слова. Увеличивая статистическую информацию, доступную программе, мы получим более надежное основание для алгоритмических решений, но все равно эти решения должен проверить человек. Помимо указанных алгоритмов в вашей программе должны быть реализованы средства, позволяющие подтвердить обоснованность выводов, которые делает программа. Один хороший способ обеспечить такую оценочную функцию — написать программу в рамках какой-либо диалоговой системы, чтобы программа и пользователь смогли совместно обсудить качество каждого решения до того, как оно будет окончательно принято. «Обсуждение» обычно состоит в том, что программа сообщает человеку факты, говорящие в пользу того или иного возможного решения, а человек либо принимает его, либо отвергает, после чего вычисление может быть продолжено.
Несмотря на то что алгоритмы неоднозначны и такая расплывчатость обычно порождает у программиста чувство неуверенности, эту программу легко проверить. Первой частью работы, по-видимому, должна быть программа шифровки, которая воспринимает в качестве исходных данных русский текст и, выбрав некоторым случайным образом смешанный алфавит и ключевое слово, выдает квадрат Виженера и печатает зашифрованный текст в стандартном пятибуквенном формате. Пробелы и пунктуация должны убираться из текста автоматически. Эта программа должна уметь также воспринимать в качестве возможных параметров квадрат Виженера и ключевое слово, чтобы можно было повторно проверять отдельные особенности работы программы расшифровки. Помните о том, что для хорошего статистического поведения алгоритмов необходимо, чтобы сообщение было в 30–40 раз длиннее ключевого слова.
Инструментовка. Эта задача прямо-таки создана для языка типа Снобол, в котором средства работы с текстовыми данными сочетаются с простыми арифметическими операциями. Хорошим кандидатом может быть и какой-нибудь другой язык, с более широким диапазоном алгебраических вычислений и с достаточными средствами обработки текстовых данных, например PL/I, Паскаль или XPL. Но какой бы язык вы ни выбрали, постарайтесь избежать представления литер целыми числами; требования машинного представления не должны навязывать некрасивое, путаное решение задачи.
Длительность исполнения. Одному исполнителю на 2 недели.
* Партия переводчика. При переводе на русский язык зашифрованного примера надо было сначала расшифровать его. Попытка сделать это с помощью описанной процедуры не привела к успеху. После небольшого размышления стало ясно, что наш ключ не подходит потому, что он от другого замка! Действительно, предлагаемый автором способ определения относительных сдвигов столбцов с помощью величин Ri, j, r исходит из того, что два столбца отличаются, кроме случайных отклонений, циклическим сдвигом на величину, равную разности номеров двух букв ключевого слова. Это свойство будет иметь место, если несколько изменить способ шифрования. В нашем случае вместо Ri, j, r следует использовать числа pi, j, r, вычисляемые, как описано ниже.
Пусть число букв алфавита равно n. Будем обозначать i-ю букву алфавита xi или yi в зависимости от того, идет речь об исходном тексте или о зашифрованном. Нам известны средняя частота pi = = p(xi) появления i-й буквы в русском языке, число fk, i появлений i-й буквы в k-й группе зашифрованного текста, общее число Nk букв в k-й группе. Определим вероятности pk(yj|xi) появления фактического числа букв fk, j, если буква yj в k-й группе обозначает букву xi исходного текста. Эти вероятности подчиняются биномиальному распределению.
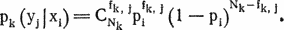
Далее найдем по формуле Байеса вероятности pk(xi|yj) того, что буква уj в k-й группе означает букву xi исходного текста. Априорные вероятности гипотез примем равными 1/n.
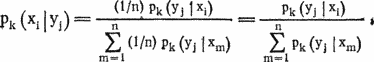
Рассмотрим теперь пару групп (столбцов табл. 24.1) k и l. Будем говорить, что между ними имеется сдвиг r, если каждой букве yj зашифрованного текста в 1-й группе соответствует буква исходного текста на r большая (по модулю n), чем в k-й группе. Это означает, что в ключевом слове 1-я буква на r меньше k-й. Для оценки вероятностей pk, l, r того, что между k-й и l-й группами имеется сдвиг r, вычислим величины
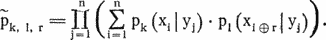
Символы ?, ? означают сложение и вычитание по модулю n. Величина рк, i г есть вероятность фактического распределения числа появлений букв при условии, что имеет место сдвиг r. Здесь не учитывается, что разные yj соответствуют разным Значения pk, l, r получаются по формуле Байеса
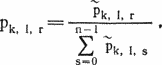
Фактический сдвиг r(k, l) между k-й и l-й группами должен иметь довольно большую вероятность pk, l, r. Но насколько большую? В следующей таблице приведены данные о расшифровке оригинала примера.

В клетке с координатами k, l указано, какое место в порядке убывания pk, l, r для фиксированных k и l занимает фактический сдвиг r(k, l). Видно, что за двумя исключениями номер места не превышает шести. Таким образом, величины сдвигов r(k, l) следует искать среди тех, которые дают 6–7 наибольших значений pk, l, r для данных k и l. Для выбора из них фактических величин сдвига следует воспользоваться согласованностью сдвигов r(k, l) ? r(l, n) = r(k, m). Складывая всех кандидатов для r(1, 2) с r(2, 3) и проверяя, находится ли результат среди кандидатов для r(1, 3), можно отбросить большую часть вариантов. Затем следует аналогично определить r(1, 4), учитывая r(2, 4) и r(3, 4), и т. д. Этот перебор легко провести вручную, если число кандидатов для каждого r(k, l) не более 8. Поскольку возможны исключительные случаи (r(3, 5) и r(4, 5) в приведенной выше таблице), то в результате этого процесса сдвиг для какой-либо группы может оказаться определенным неправильно либо процесс может вообще не сойтись (будут отброшены все варианты). В таком случае следует заново определить величину сдвига для наихудшей группы (определяемой, например, по наибольшему среднему месту для сдвигов относительно этой группы), учитывая большее число кандидатов.
После определения сдвигов следует найти ключевое слово, как описано в основном тексте, рассматривая все слова вида xa, xa ? r(1, 2), xa ? r(1, 3), … (а = 1, …, n). Возможно, для получения осмысленного слова придется изменить одну из букв. Определив ключевое слово, находим окончательные величины сдвигов.
Теперь для определения перестановки вычислим вероятности p(xi|yj) того, что буква yj в зашифрованном тексте соответствует букве xi в первой группе, xi ? r(1, 2) — во второй и т. д.:
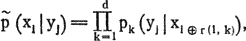
(r(1, 1) полагаем равным нулю, d — число групп)
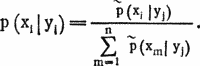
Фактические значения xi должны давать большие значения p(xi|yj). Числа p(xi|yj) дают для определения перестановки существенно более четкую информацию, чем числа pk,l, r для определения сдвигов. Оказывается, что при длине текста около 700 букв для большинства букв yj зашифрованного текста соответствующие им xi дают максимальное значение p(xi|yj). Перестановка легко уточняется, если начать расшифровку, учитывая осмысленность получаемого текста.
При реализации этого алгоритма на ЭВМ следует иметь в виду, что числа p?k, l, r могут оказаться весьма малыми. Так, при расшифровке оригинала примера они лежали в диапазоне от 10?51 до 10?36. Если на вашей ЭВМ такие числа непредставимы, то вычислите логарифмы log p?k, l, r. Числа pk, l, r и p(xi|yj) можно не вычислять, воспользовавшись вместо них pk, l, r и p(xi|yj), отличающимися постоянным множителем.
Этот способ позволил расшифровать английский оригинал примера. Удастся ли вам проделать то же с русским текстом?
- WEP-шифрование
- 5.2. Шифрование
- 5.2.3. Шифрование файлов
- Календарный шифр
- Шифры перестановки
- Усовершенствованный книжный шифр
- Использование стандартного шифрования.
- PGP: Кодирование и шифрование информации с открытым ключом.
- Посылка зашифрованного текста через каналы электронной почты: формат Radix-64.
- 10.4. Шифрование в Windows 7
- Новые системы шифрования
- Шифрование сценариев




