Книга: ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

2.6.1. Успешное доказательство конъюнкции целевых утверждений

2.6.1. Успешное доказательство конъюнкции целевых утверждений

Пролог пытается согласовать с базой данных входящие в конъюнкцию целевые утверждения в том порядке, в каком они написаны (слева направо), где бы они ни появились – в теле правила или в вопросе. Это означает, что Пролог не будет проверять некоторое утверждение, пока не будет доказан его сосед слева. А сосед справа будет рассматриваться только после доказательства данного целевого утверждения. Рассмотрим следующую простую программу о семейных связях:

родители (С,M,F):- мать(С,М), отец(C,F).

мать(джон,анна).

мать(мэри,анна).

отец(мэри,фред). отец(джон,фред).

Давайте рассмотрим последовательность событий, позволяющую дать ответ на вопрос:

?-женщина(мэри), родители(мэри,М,Р), родители(джон,М,Р).

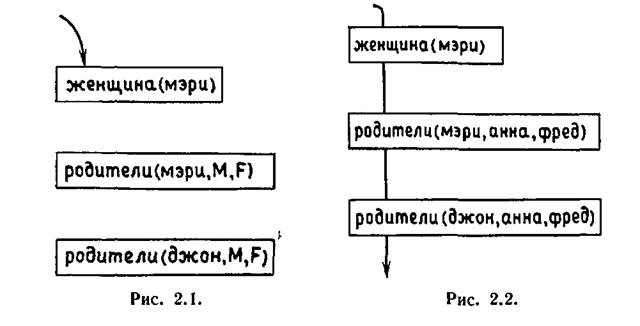
Данный вопрос позволяет определить, является ли мэри сестрой джона. Для того чтобы дать ответ Прологу, необходимо согласовать с базой данных последовательность подцелей, приведенных на рис. 2.1.

Представим целевые утверждения в виде прямоугольников, распределенных по странице. Стрелка, начинающаяся в верхней части страницы, указывает, какие целевые утверждения уже согласованы. Прямоугольники, через которые стрелка уже прошла, соответствуют согласованным целевым утверждениям. Прямоугольники, лежащие ниже острия стрелки, соответствуют целевым утверждениям, которые Пролог еще не рассматривал. При выполнении программы стрелка движется вверх и вниз по странице в соответствии с переходом Пролога от одного целевого утверждения к другому. Будем называть ее цепочкой доказательств. В данном примере стрелка начинается в верхней части страницы, как показано выше. По мере согласования трех целевых утверждений она будет удлиняться вниз, проходя через соответствующие прямоугольники. Конечная ситуация представлена на рис. 2.2. Отметим, что в ходе доказательства согласованности целевых утверждений с базой данных были найдены значения для переменных М и F.

Такая диаграмма иллюстрирует общую структуру происходящего, но она не показывает, как доказывались эти три целевых утверждения. Для того чтобы показать это, поместим внутрь прямоугольников больше информации. Давайте посмотрим, как доказывалось второе целевое утверждение. Доказательство согласованности целевого утверждения с базой данных включает в себя поиск в базе данных соответствующих (сопоставимых) утверждений, пометку этого места базы данных и затем доказательств возникших подцелей. Этот процесс для второго целевого утверждения можно проиллюстрировать, включив в прямоугольник родители индикацию выбранного утверждения и возникшие подцели. Выбранное утверждение обозначается числом в скобках, в данном случае (1). Это число указывает номер выбранного утверждения в наборе утверждений с соответствующим предикатом. Таким образом, число 1 означает, что было выбрано первое утверждение с данным предикатом. Эта информация достаточна для отметки места в базе данных. Подцели заключены в маленькие прямоугольники, помещенные в прямоугольник данного целевого утверждения. В момент, когда выбрано утверждение родители, ситуация выглядит так, как показано на рис. 2.3.

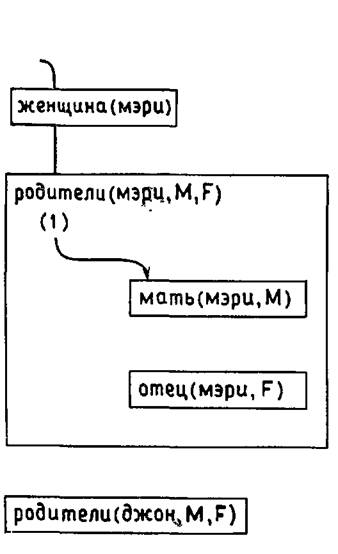
Рис. 2.3.

Стрелка вошла в прямоугольник родители и прошла через скобки, указывая, что выбрано некоторое утверждение. Данное утверждение создало две подцели – мать и отец. В данный момент для получения ответа на вопрос необходимо, чтобы стрелка прошла через два маленьких прямоугольника, вышла из прямоугольника родители и затем прошла через второй прямоугольник родители. Когда стрелка проходит через маленькие прямоугольники, необходимо выполнить те же самые шаги: выбор соответствующего утверждения и доказательство порождаемых им подцелей. В данном примере для каждого из этих двух целевых утверждений в базе данных находится соответствующий факт, и их согласованность с базой данных доказывается. На рис. 2.4 приведено более детальное изображение ситуации в момент получения ответа на вопрос.

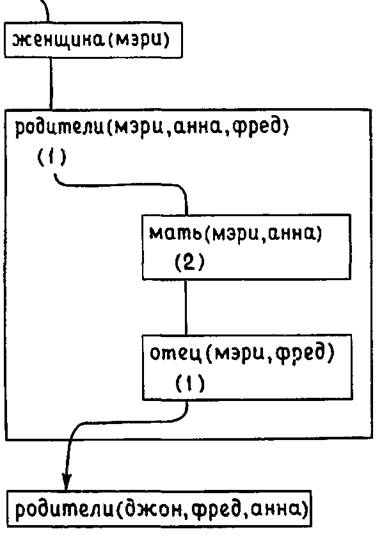
Рис. 2.4.

Отметим, что для полноты картины нам необходимо было бы показать, как доказываются целевые утверждения женщина(мэри) и родители(джон,анна,фред). Однако столь подробная диаграмма не поместилась бы на одной странице.

Данный пример иллюстрирует общую схему рассмотрения целевых утверждений, объединенных в конъюнкцию, для случая, когда все цели согласуются с базой данных. Стрелка перемещается вниз по странице, по очереди проходя через прямоугольники. Когда стрелка входит в какой-либо прямоугольник, выбирается некоторое утверждение и отмечается его позиция. Если данное утверждение сопоставимо с целью и является фактом, стрелка может покинуть прямоугольник (такая ситуация имела место для целевых утверждений мать и отец). Если же утверждение сопоставимо с целью, но является правилом, создаются прямоугольники для подцелей, и стрелка должна пройти через них, прежде чем она сможет покинуть первоначальный прямоугольник.

Оглавление книги