Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Квантовое состояние частицы
Квантовое состояние частицы
Как выглядит «физическая реальность» на квантовом уровне, где различные «альтернативные возможности», открытые перед системой, должны всегда обладать способностью сосуществовать, образуя суммы со странными комплекснозначными весами? Многие физики впадают в отчаяние при виде такой картины. Вместо этого они призывают рассматривать квантовую теорию только в качестве вычислительной процедуры для расчета вероятностей, а не объективной картины физического мира. Некоторые из них вполне серьезно заявляют, что квантовая теория проповедует невозможность получения объективной картины, по крайней мере той, которая согласуется с физическими фактами. Я же считаю такой пессимизм совершенно необоснованным. Во всяком случае было бы преждевременно на основании сказанного выше принять подобную точку зрения. Позднее мы рассмотрим некоторые из наиболее поразительных следствий квантовых эффектов, что возможно позволит нам понять причины такого отчаяния. Но пока давайте смотреть на вещи более оптимистично и мужественно встретим все, что уготовила нам квантовая теория.
Первым предстанет перед нами квантовое состояние. Попытаемся мысленно представить себе одну-единственную квантовую частицу. Классически, частица определяется своим положением в пространстве, и для того, чтобы узнать, что произойдет с частицей дальше, нам также необходимо знать ее скорость (или, что эквивалентно, ее импульс). Квантовомеханически, любое положение, которое может занимать частица, является лишь одной их возможных «альтернатив» для частицы. Мы уже видели, что все альтернативы должны каким-то образом объединяться вместе с комплекснозначными весами. Набор этих комплекснозначных весов описывает квантовое состояние частицы. Обычно в квантовой теории принято использовать греческую букву ? (произносится: «пси») для обозначения такого набора весов. Этот набор весов, рассматриваемый как комплекснозначная функция положения частицы, называется волновой функцией частицы. Для каждого положения х волновая функция принимает вполне определенное значение ?(х) — амплитуду вероятности того, что частица находится в положении х. Мы можем использовать одну букву ? для обозначения квантового состояния как единого целого. Я разделяю ту точку зрения, что квантовое состояние ? частицы — это и есть ее физически реальное положения в пространстве.
Каким же образом можно наглядно изобразить комплексную функцию ? ? Сделать это сразу для всего трехмерного пространства несколько затруднительно, поэтому мы немного упростим задачу и предположим, что наложенные связи позволяют частице двигаться только вдоль одномерной линии — например, оси х обычной (декартовой) системы координат. Если бы функция ? была вещественной, то мы могли бы представить себе ось y, перпендикулярную оси х, и построить график функции ? (рис. 6.10а).
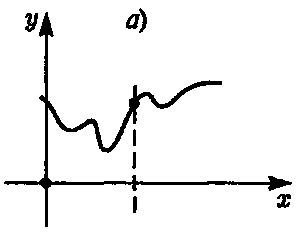
Рис. 6.10.а) График действительной функции действительной переменной х
Но в данном случае для изображения значения комплексной функции ? нам требуется «комплексная ось у» — плоскость Аргана. Для этой цели вообразим, что мы можем использовать два других пространственных измерения: например, у-направление в качестве действительной оси плоскости Аргана, а z-направление — как мнимую ось. Для получения правильной картины волновой функции мы можем изобразить ?(х) (значение функции в точке х) точкой на этой плоскости Аргана (т. е. на плоскости yz, проходящей через каждую точку оси х). Когда положение точки х изменяется, то изменяется также и положение точки на плоскости Аргана. При этом точка описывает некоторую кривую в пространстве, извивающуюся вокруг оси х (рис. 6.10 b).
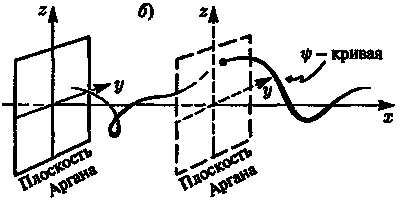
Рис. 6.10.б) график комплексной функции V действительной переменной х
Назовем эту кривую ? — кривой рассматриваемой частицы. Если бы мы поместили в некоторой точке х детектор, то вероятность обнаружить частицу в данной точке можно найти, вычислив квадрат модуля амплитуды ?(х), т. е.
|?(x)|2
равный квадрату расстояния ?-кривой от оси x[143].
Чтобы изобразить подобным образом волновую функцию, определенную на всем трехмерном физическом пространстве, понадобилось бы пять измерений: три — для физического пространства и два — для плоскости Аргана в каждой точке, в которой мы строим график функции ?(х). Однако наша упрощенная картина еще нам пригодится. Если мы захотим изучить поведение волновой функции вдоль произвольного направления в физическом пространстве, то для этого необходимо просто выбрать ось х вдоль этой линии, а два других пространственных измерения временно использовать в качестве действительной и мнимой осей на плоскости Аргана. Этот способ поможет нашему осмыслению эксперимента с двумя щелями.
Как я упоминал выше, в классической физике для того, чтобы определить, что будет происходить дальше, необходимо знать скорость (или импульс) частицы. В квантовой механике нам представляется значительная экономия. Волновая функция ? уже содержит различные амплитуды для различных возможных импульсов! (Кое-кто из недовольных читателей может возразить, что «самое время» говорить об экономии, если принять во внимание, как сильно нам пришлось усложнить простую классическую картину точечной частицы. Хотя я во многом согласен с таким читателем, я все же советую не отвергать те лакомые кусочки, которые ему преподносят, ибо худшее еще впереди!) Каким образом амплитуды скоростей определяются волновой функцией ?? На самом же деле лучше думать в терминах амплитуд импульсов. (Напомним, что импульс, или количество движения, равен скорости, умноженной на массу частицы, см. гл.6 «Уравнение Шредингера; уравнение Дирака») Для этого следует применить к волновой функции ? так называемый гармонический анализ. Подробно объяснять здесь, что это такое, было бы неуместно, скажу только, что он тесно связан с тем, что происходит с музыкальными звуками. Волну любой формы можно разложить в сумму различных «гармоник» (отсюда и термин «гармонический анализ»), которые представляют собой чистые тона различной высоты (т. е. с различными частотами). В случае волновой функции ? «чистые тона» соответствуют различным возможным значениям импульса, которые может иметь частица, а величина вклада каждого «чистого тона» в ? определяет амплитуду соответствующего значения импульса. Сами «чистые тона» называются импульсными состояниями.
Как выглядит импульсное состояние, представленное ? — функцией? Оно похоже на кривую, напоминающую по форме штопор, официальное математическое название которой — винтовая линия (рис. 6.11)[144].

Рис. 6.11. Импульсное состояние имеет ?-кривую в форме штопора
Штопоры с частыми витками соответствуют большим импульсам, а штопоры, которые едва вращаются, — очень малым импульсам. Существует предельный случай, когда ?-кривая вообще не делает витков и вырождается в прямую в случае нулевого импульса. В поведении винтовой линии неявно скрыто знаменитое соотношение Планка. Так как энергия Е всегда пропорциональна частоте v(Е = hv), то частые витки означают короткую длину волны, большую частоту и, следовательно, большой импульс и высокую энергию, а редкие витки означают малую частоту и низкую энергию. Если плоскости Аргана ориентированы обычным способом (т. е. когда оси х, у, z образуют, как описано выше, правую тройку), то импульсы, направленные в положительном направлении оси х, соответствуют правым штопорам (которые обычно и используются).
Иногда квантовые состояния полезно описывать не в терминах обычных волновых функций, как это было сделано выше, а в терминах волновых функций импульсов. Это сводится к рассмотрению разложения волновой функции ? по различным импульсным состояниям и построению новой функции ??, зависящей на этот раз не от положения х, а от импульса р; значение ??(p) при любом р задает величину вклада состояния с импульсом р в ?-функцию. (Пространство величин р называется импульсным пространством.) Смысл ?? состоит в том, что при каждом конкретном выборе р комплексное число ??(р) задает амплитуду того, что частица имеет импульср.
Существует математическое название для соотношения между функциями ? и ??. Каждая из этих функций называется преобразованием Фурье другой — в честь французского инженера и математика Жозефа Фурье (1768–1830). Я ограничусь здесь лишь несколькими замечаниями по поводу преобразования Фурье. Первое замечание: между ? и ?? существует замечательная симметрия. Чтобы перейти от ? назад к ??, мы по существу прибегаем к той же процедуре, которую использовали при переходе от ? к ??. Теперь ?? становится объектом гармонического анализа. «Чистые тона» (т. е. штопоры в пространстве импульсов) на этот раз называются конфигурационными состояниями. Каждое положение х определяет такой «чистый тон» в пространстве импульсов, а величина такого вклада «чистого тона» в ? дает значение ?(x).
Конфигурационное состояние соответствует (в терминах обычного пространства) некоторой функции ?, имеющей острый пик в рассматриваемой точке х, а это значит, что все амплитуды равны нулю, за исключением амплитуды в данной точке. Такая функция называется дельта-функцией (Дирака), хотя, строго говоря, это — не совсем «функция» в обычном смысле, так как ее значение в точке х бесконечно велико. Аналогичным образом импульсные состояния (винтовые линии в конфигурационном пространстве) порождают дельта-функции в пространстве импульсов (рис. 6.12). Таким образом, оказывается, что преобразование Фурье винтовой линии есть дельта-функция и наоборот!
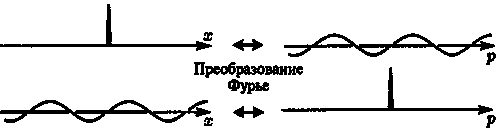
Рис. 6.12. Дельта-функция в конфигурационном пространстве переходит в штопор в импульсном пространстве и наоборот
Описание в терминах конфигурационного пространства полезно всякий раз, когда требуется произвести измерение возможного положения частицы в пространстве, которое сводится к увеличению до классического уровня эффектов различных возможных положений частицы. (Грубо говоря, фотоэлементы и фотографические пластинки осуществляют измерение положения фотонов в пространстве.) Описание на языке импульсного пространства полезно, когда требуется измерить импульс частицы, т. е. увеличить до классического уровня эффекты различных возможных импульсов. (Эффекты отдачи или дифракции на кристаллах могут быть использованы для измерений импульса.) В каждом случае квадрат модуля соответствующей волновой функции (? или ??) дает искомую вероятность результата производимого измерения.
В заключение этого раздела обратимся еще раз к эксперименту с двумя щелями. Мы узнали, что согласно квантовой механике даже одна частица сама по себе должна обладать волновым поведением. Такая волна описывается волновой функцией ?. Более всего похожи на волны волновые функции импульсных состояний. В эксперименте с двумя щелями мы рассматривали фотоны с определенной частотой; так что волновая функция фотона состояла из импульсных состояний различных направлений, в которых расстояние между соседними витками штопора — длина волны — было одно и то же на протяжении всей винтовой линии. (Длина волны определяется частотой.)
Волновая функция каждого фотона распространяется первоначально из источника в точке S и (если мы не следим за прохождением фотона через щели) проходит к экрану через обе щели. Однако только небольшая часть волновой функции проходит через щели, поэтому мы можем мысленно рассматривать щели как новые источники, каждый из которых по отдельности испускает волновую функцию. Эти две части волновой функции интерферируют одна с другой так, что когда они доходят до экрана, в одних его точках они суммируются, а в других погашают друг друга. Чтобы выяснить, где волны суммируются и где гасят друг друга, выберем на экране некоторую точку р и рассмотрим прямые, проведенные к точке р от каждой из щелей t u b. Вдоль отрезка tp мы имеем одну винтовую линию, а вдоль отрезка bр — другую винтовую линию. (Мы также имеем винтовые линии вдоль линий st и sb, но если предположить, что источник находится на одном и том же расстоянии от обеих щелей, то на пути к щелям винтовые линии успеют совершить одинаковое число витков.) Число витков, которые винтовые линии совершат к тому моменту, когда они достигнут экран в точке р, зависит от длины отрезков tp и bр. Если эти длины отличаются на целое число длин волн, то в точке р винтовые линии окажутся совмещенными в одном направлении относительно своих осей (т. е. ? = 0°, где ? определено в предыдущем разделе), так что соответствующие амплитуды сложатся и дадут яркое пятно. Если же эти линии отличаются по длине на целое число длин волн плюс половина длины волны, то в точке р винтовые линии окажутся совмещенными в противоположных направлениях относительно своих осей (? = 180°), поэтому соответствующие амплитуды погасят друг друга, и мы получим темное пятно. Во всех остальных случаях между смещениями винтовых линий в точке р образуется некоторый угол, поэтому соответствующие амплитуды будут суммироваться некоторым промежуточным образом, и мы получим пятно с промежуточной интенсивностью освещенности (рис. 6.13).
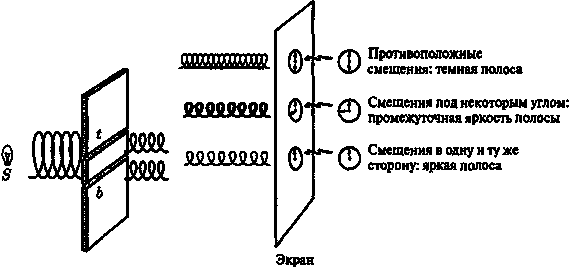
Рис. 6.13. Анализ эксперимента с двумя щелями в терминах штопорообразного представления импульсных состояний фотона
- Нужна ли философам квантовая теория?
- Проблемы с классической теорией
- Начало квантовой теории
- Эксперимент с двумя щелями
- Амплитуды вероятностей
- Квантовое состояние частицы
- Принцип неопределенности
- Эволюционные процедуры U и R
- Одна частица — сразу в двух местах?
- Гильбертово пространство
- Измерения
- Спин и сфера Римана состояний
- Объективность и измеримость квантовых состояний
- Копирование квантового состояния
- Спин фотона
- Объекты с большим спином
- Многочастичные системы
- «Парадокс» Эйнштейна, Подольского и Розена
- Эксперименты с фотонами: проблема для специальной теории относительности?
- Уравнение Шредингера; уравнение Дирака
- Квантовая теория поля
- Кошка Шредингера
- Различные точки зрения на существующую квантовую теорию
- К чему мы пришли после всего сказанного?




