Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Построение множества Мандельброта
Построение множества Мандельброта
Теперь мы можем рассмотреть, как определяется множество Мандельброта. Пусть z — это некоторое произвольное комплексное число. Каковым бы ни было это число, оно представляется некоторой точкой на плоскости Аргана. Рассмотрим теперь отображение, при котором z превращается в новое комплексное число, равное
z ? z2 + с,
где с есть некое фиксированное (то есть заданное) комплексное число. Числу z2 + с будет сопоставляться некоторая другая точка на плоскости Аргана. Например, если с равно числу 1,63 — i4,2, то z отображается согласно формуле
z ? z2 + 1,63 — i4,2,
так что, в частности, число 3 превратится в
З2 +1,63 — i4,2 = 9+1,63 — i4,2 = 10,63 — i4,2,
а число -2,7 + i0,3 в
(-2,7 + i0,3)2 + 1,63 — i4,2 =
= (-2,7)2 — (0,3)2 + 1,63 +
+ i{(-2,7)(0,3) — 4,2} = 8,83 — i5,82.
Когда числа становятся громоздкими, вычисления лучше выполнять на компьютере.
Теперь, каково бы ни было число c, число 0 превращается, согласно принятой схеме, в число с. А что же можно сказать о самом числе с? Оно превращается в с2 + с. Давайте продолжим этот процесс, применив наше преобразование к с2 + с. Мы получим:
(с2 + с)2 + с = с + 2 с + с2 + с.
Снова повторим отображение, применив его к приведенному выше числу. Мы получим:
(с4 + 2 с3 + с2 + с)2 + с =
= с8 + 4с7 + 6 с6 + 6с5 + 5с4 + 2 с3 + с2 + с.
Потом еще раз применим процедуру, теперь уже к последнему числу, и т. д. В результате мы получаем последовательность комплексных чисел, которая начинается с числа 0:
0, с, с2 + с, с4 + 2с3 + с2 + с…
Данная процедура, будучи реализована при некоторых определенных значениях комплексного числа с, дает последовательность чисел, которые все время остаются вблизи начала координат плоскости Аргана; точнее, для выбранных таким образом значений с получаемая последовательность оказывается ограниченной, то есть любой ее член находится в пределах некоторого фиксированного круга с центром в начале координат (рис. 3.12).
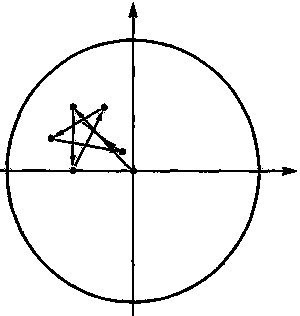
Рис. 3.12. Последовательность точек на плоскости Аргана ограничена, если вся она целиком помещается в пределах некоторого фиксированного круга. (Итерация на рисунке начинаетсл с точки 0 и построена для с = — l/2 + (l/2)i.)
Хорошим примером здесь может служить последовательность с = 0, поскольку каждый ее член равен 0. Другим примером ограниченного поведения является случай с = 1, при котором получается последовательность 0, -1, 0, -1, 0, -1….; еще один пример — это с = i, когда получается последовательность 0, i, i — 1, -i, i — 1, -i, i — 1, -i….. Однако, для целого ряда других комплексных чисел с получаемая последовательность все дальше удаляется от начала координат, то есть является неограниченной и не может находиться целиком в пределах фиксированного круга. Именно так происходит при с = 1, когда получается последовательность 0, 1, 2, 5, 26, 677,458 330….; аналогичное поведение имеет место в случае с = 3 — соответствующая последовательность имеет вид 0, -3, 6, 33,1086….; а также случай с = i — 1, который приводит к последовательности 0, i — 1, -i — 1, -1 + 3i, — 9 — i5, 55 + i91, -5257 + i10011,
Множество Мандельброта — то есть зачерненная часть страны Тор'Блед-Нам[64] — как раз и есть та самая область на плоскости Аргана, что состоит из всех точек с, для которых получаемая последовательность является ограниченной. Белая же область состоит из тех точек с, для которых получается неограниченная последовательность. Приведенные выше подробные рисунки основаны на результатах компьютерных вычислений. На компьютере был проведен систематический перебор всевозможных комплексных чисел с, для каждого из них строилась последовательность 0, с, с2+с…, после чего согласно некоторому критерию определялось, ограничена или нет получаемая последовательность. Если последовательность оказывалась ограниченной, то соответствующая числу с точка экрана становилась черной. Таким образом, для каждой точки в рассматриваемой области компьютер решал, закрасить ее в белый или черный цвет.
Множество Мандельброта впечатляет своей сложностью, особенно учитывая, как это часто бывает в математике, удивительную простоту его определения. Кроме того, структура этого множества в целом не очень чувствительна к выбору алгебраической формы отображения — z ? z2 + с. Многие другие итеративные отображения (например, z ? z3 + iz2 + c) приводят к поразительно похожим структурам (при условии выбора подходящего начального числа — возможно, это не 0, а значение, четко задаваемое вполне определенным математическим правилом для каждого разумно выбранного отображения). Подобные «мандельбротовы» структуры характеризуются некоторыми универсальными или абсолютными свойствами по отношению к итеративным комплексным отображениям. Изучение таких структур является предметом отдельного раздела математики — так называемой теории комплексных динамических систем.
- Определение целей. Построение цепочек
- Операции с множествами узлов
- 4.2. Создание трехмерной модели и построение горизонтальной проекции детали
- Построение модели выходов (результатов)
- Глава 9 Построение отказоустойчивых систем
- Построение и диаграмм
- Практическая работа 49. Построение и форматирование диаграмм
- Практическая работа 57. Построение запросов
- Построение отчетов
- Построение диаграммы на основе данных нескольких рабочих листов
- Построение пути сертификации
- Построение структуры веб-страницы




