Книга: Учебное пособие по курсу «Нейроинформатика»
Элементы самодвойственных сетей
Разделы на этой странице:
Элементы самодвойственных сетей
Если при обратном функционировании самодвойственной сети на ее выход подать производные некоторой функции F по выходным сигналам сети, то в ходе обратного функционирования на входах параметров сети должны быть вычислены элементы градиента функции F по параметрам сети, а на входах сигналов — элементы градиента функции F по входным сигналам. Редуцируя это правило на отдельный элемент, получаем следующее требование к обратному функционированию элемента самодвойственной сети: Если при обратном функционировании элемента самодвойственной сети на его выход подать производные некоторой функции F по выходным сигналам элемента, то в ходе обратного функционирования на входах параметров элемента должны быть вычислены элементы градиента функции F по параметрам элемента, а на входах сигналов — элементы градиента функции F по входным сигналам элемента. Легко заметить, что данное требование автоматически обеспечивает подачу на выход элемента, предшествующего данному, производной функции F по выходным сигналам этого элемента.
Далее в этом разделе для каждого из элементов, приведенных на рис. 1 определены правила обратного функционирования, в соответствии со сформулированными выше требованиями к элементам самодвойственной сети.
Синапс
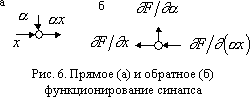
У синапса два входа — вход сигнала и вход синаптического веса (рис. 6а). Обозначим входной сигнал синапса через x, а синаптический вес через ?. Тогда выходной сигнал синапса равен ?x. При обратном функционировании на выход синапса подается сигнал ?F/?(?x).
На входе синапса должен быть получен сигнал обратного функционирования, равный
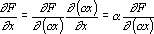
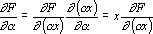
Умножитель
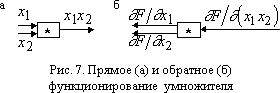
Умножитель имеет два входных сигнала и не имеет параметров. Обозначим входные сигнал синапса через x1, x2. Тогда выходной сигнал умножителя равен x1x2 (рис. 7а). При обратном функционировании на выход умножителя подается сигнал ?F/?(x1x2). На входах сигналов x1 и x2 должны быть получены сигналы обратного функционирования, равные
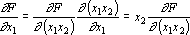
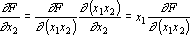
Точка ветвления
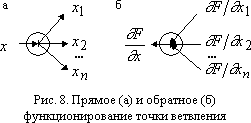
В отличие от ранее рассмотренных элементов, точка ветвления имеет только один вход и несколько выходов. Обозначим входной сигнал через x, а выходные через x1, x2, …, xn, причем xi=x (рис. 8а). При обратном функционировании на выходные связи точки ветвления подаются сигналы
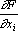
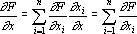
Сумматор
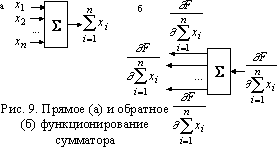
Сумматор считает сумму входных сигналов. Обычный сумматор не имеет параметров. При описании прямого и обратного функционирования ограничимся описанием простого сумматора, поскольку функционирование адаптивного и квадратичного сумматора может быть получено как прямое и обратное функционирование сети в соответствии с их схемами, приведенными на рис. 3б и 3в. Обозначим входные сигналы сумматора через x1, x2, …, xn(рис. 9а). Выходной сигнал равен
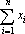
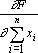
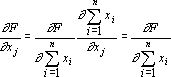
Из последней формулы следует, что все сигналы обратного функционирования, выдаваемые на входные связи сумматора, равны. Таким образом сумматор при обратном функционировании переходит в точку ветвления, или, другими словами, сумматор является двойственным по отношению к точке ветвления.
Нелинейный Паде преобразователь
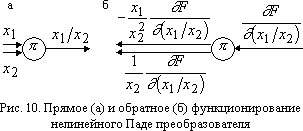
Нелинейный Паде преобразователь или Паде элемент имеет два входных сигнала и один выходной. Обозначим входные сигналы через x1, x2. Тогда выходной сигнал Паде элемента равен x1/x2 (рис. 10а). При обратном функционировании на выход Паде элемента подается сигнал ?F/?(x1/x2).
На входах сигналов x1 и x2 и должны быть получены сигналы обратного функционирования, равные
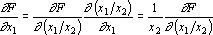
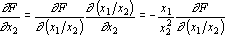
Нелинейный сигмоидный преобразователь
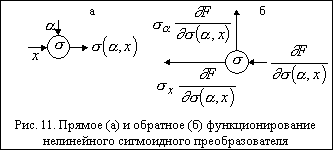
Нелинейный сигмоидный преобразователь или сигмоидный элемент имеет один входной сигнал и один параметр. Сторонники чистого коннекционистского подхода считают, что обучаться в ходе обучения нейронной сети могут только веса связей. С этой точки зрения параметр сигмоидного элемента является не обучаемым и, как следствие, для него нет необходимости вычислять поправку. Однако, часть исследователей полагает, что нужно обучать все параметры всех элементов сети. Исходя из этого, опишем вычисление этим элементом поправки к содержащемуся в нем параметру.
Обозначим входной сигнал через x, параметр через ?, а вычисляемую этим преобразователем функцию через ?(?,x) (рис. 11а). При обратном функционировании на выход сигмоидного элемента подается сигнал ?F/??(?,x).
На входе сигнала должен быть получен сигнал обратного функционирования, равный
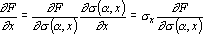
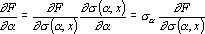
Произвольный непрерывный нелинейный преобразователь
Произвольный непрерывный нелинейный преобразователь имеет несколько входных сигналов, а реализуемая им функция зависит от нескольких параметров. Выходной сигнал такого элемента вычисляется как некоторая функция ?(x,?), где x — вектор входных сигналов, а a — вектор параметров. При обратном функционировании на выходную связь элемента подается сигнал обратного функционирования, равный ?F/??.
На входы сигналов выдаются сигналы обратного функционирования, равные
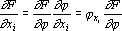
Пороговый преобразователь
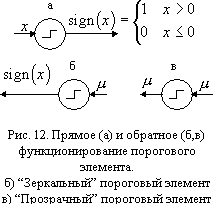
Пороговый преобразователь, реализующий функцию определения знака (рис. 12а), не является элементом с непрерывной функцией, и, следовательно, его обратное функционирование не может быть определено из требования вычисления градиента. Однако, при обучении сетей с пороговыми преобразователями полезно иметь возможность вычислять поправки к параметрам. Так как для порогового элемента нельзя определить однозначное поведение при обратном функционировании, предлагается доопределить его, исходя из соображений полезности при конструировании обучаемых сетей. Основным методом обучения сетей с пороговыми элементами является правило Хебба (подробно рассмотрено во второй части главы). Оно состоит из двух процедур, состоящих в изменении «весов связей между одновременно активными нейронами». Для этого правила пороговый элемент при обратном функционировании должен выдавать сигнал обратного функционирования, совпадающий с выданным им сигналом прямого функционирования (рис. 12б). Такой пороговый элемент будем называть зеркальным. При обучении сетей Хопфилда [312], подробно рассмотренном во второй части главы, необходимо использовать «прозрачные» пороговые элементы, которые при обратном функционировании пропускают сигнал без изменения (рис. 12в).
- Методы построения двойственных сетей
- Конструирование нейронных сетей
- 6.4. Рабочий лист Excel и его структурные элементы
- Тексты для блогов и соцсетей
- 4.4. Логические элементы и синтез логических схем
- 4.7 Структурные элементы SAN
- ЭМУЛЯЦИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.6 Файловые системы для сетей хранения данных
- Вложение файлов в элементы списков
- Логические элементы
- 5.2. Основные приемы работы, элементы текстового редактора
- Правило 16. Группируйте связанные между собой элементы




