Книга: Учебное пособие по курсу «Нейроинформатика»

Усреднение по обучающему множеству

Усреднение по обучающему множеству

Показатель значимости параметра X^qpзависит от точки в пространстве параметров, в которой он вычислен и от примера из обучающего множества. Существует два принципиально разных подхода для получения показателя значимости параметра, не зависящего от примера. При первом подходе считается, что в обучающей выборке заключена полная информация о всех возможных примерах. В этом случае, под показателем значимости понимают величину, которая показывает насколько изменится значение функции оценки по обучающему множеству, если текущее значение параметра wpзаменить на выделенное значение w^•p. Эта величина вычисляется по следующей формуле:

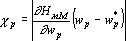
В рамках другого подхода обучающее множество рассматривают как случайную выборку в пространстве входных параметров. В этом случае показателем значимости по всему обучающему множеству будет служить результат некоторого усреднения по обучающей выборке.

Существует множество способов усреднения. Рассмотрим два из них. Если в результате усреднения показатель значимости должен давать среднюю значимость, то такой показатель вычисляется по следующей формуле:

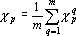
Если в результате усреднения показатель значимости должен давать величину, которую не превосходят показатели значимости по отдельным примерам (значимость этого параметра по отдельному примеру не больше чем ?p), то такой показатель вычисляется по следующей формуле:

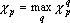
Показатель значимости (4) хорошо зарекомендовал себя при использовании в работах группы НейроКомп.

Оглавление книги